"Элегантная вселенная (суперструны, скрытые размерности и поиски окончательной теории)" - читать интересную книгу автора (Грин Брайан)
Глава 8. Измерений больше, чем видит глаз
Эйнштейн в своей специальной и общей теории относительности разрешил два основных противоречия физики последнего столетия. Хотя проблемы, послужившие побудительным мотивом его работ, вовсе не предвещали такого результата, каждое из этих решений полностью трансформировало наше понимание пространства и времени. Теория струн разрешила третий главный конфликт в физике прошлого века, причем таким способом, который, наверное, восхитил бы даже Эйнштейна, и потребовала очередного коренного пересмотра наших понятий пространства и времени. Сотрясение основ современной физики было столь сильным, что не устояли даже наши представления о числе измерений во Вселенной, казавшиеся совершенно незыблемыми и, тем не менее, подвергшиеся радикальному и убедительному изменению.
Наша интуиция питается жизненным опытом. Но этим роль опыта не ограничивается: он формирует опорный каркас, в рамках которого мы анализируем и интерпретируем полученную из окружающего мира информацию. Например, вряд ли вы будете сомневаться, что Маугли, воспитанный стаей диких волков, будет интерпретировать окружающую действительность совсем иначе, чем мы. Даже менее сильные различия, например, различия между людьми, воспитанными в существенно разных культурных традициях, подчеркивают ту роль, которую играет жизненный опыт в восприятии мира. Однако есть явления, воздействие которых испытывают
Эквивалентное утверждение, с которым мы столкнулись, рассматривая специальную теорию относительности, заключается в том, что любая точка Вселенной может быть однозначно определена тремя параметрами, указывающими ее положение в этих трех пространственных измерениях. Например, вы можете описать адрес в городе, указав стрит[65] (положение в измерении «влево-вправо»), авеню (положение в измерении «вперед-назад») и этаж (положение в измерении «вверх-вниз»). Работы Эйнштейна показали нам, что время может рассматриваться как еще одно измерение (измерение «будущее-прошлое»), что увеличивает общее число измерений до четырех (три пространственных и одно временное). Вы определяете события во Вселенной, указывая, где и когда они произошли.
Эта особенность Вселенной кажется столь фундаментальной и естественной, что обычно даже не упоминается. Тем не менее, в 1919 г. малоизвестный польский математик Теодор Калуца из Кенигсбергского университета дерзнул бросить вызов очевидному — он предположил, что в действительности Вселенная может иметь
Предположение о том, что наша Вселенная может иметь более трех пространственных измерений, может показаться бессмысленным, эксцентричным или мистическим. Однако в действительности оно является вполне реальным и тщательно обоснованным. Убедиться в этом будет проще, если на время оставить в покое Вселенную и рассмотреть более привычный объект, например длинный и тонкий Садовый шланг.
Представим, что несколько сотен метров Садового шланга протянуто поперек каньона, и мы наблюдаем его с расстояния, скажем, в километр, как показано на рис. 8.1а.
 |
Рис. 8.1. а) Садовый шланг со значительного расстояния выглядит одномерным объектом. б) При увеличении становится видимым второе измерение — то, которое имеет форму окружности, охватывающей ось шланга.
С такого расстояния хорошо видна горизонтальная протяженность длинного развернутого шланга, однако, если только вы не обладаете орлиным зрением, вам будет трудно оценить его
На самом деле известно, что у шланга
Эти два измерения явно различаются. Направление вдоль шланга является длинным, протяженным, и хорошо видимым. Направление, опоясывающее шланг, является коротким, «свернутым» и трудноразличимым. Для того чтобы узнать о существовании циклического измерения, приходится исследовать шланг с существенно большим разрешением.
Этот пример подчеркивает неочевидную и важную особенность пространственных измерений: они могут быть двух видов. Они могут быть просторными, протяженными и, вследствие этого, доступными непосредственному наблюдению, но они также могут быть маленькими, скрученными и гораздо менее поддающимися обнаружению. Конечно, в нашем примере не пришлось тратить слишком много усилий на то, чтобы обнаружить «свернутое» измерение, опоясывающее ось шланга. Вам было достаточно воспользоваться биноклем. Однако если вам придется иметь дело с очень тонким Садовым шлангом, имеющим обхват волоса или капилляра, обнаружить свернутое измерение будет не так-то просто.
В статье, которую Калуца отправил Эйнштейну в 1919 г., он высказал удивительное предположение. Калуца утверждал, что пространственная структура Вселенной может содержать больше измерений, чем три известных нам из жизненного опыта. Как мы вскоре увидим, мотивом для столь радикальной гипотезы было то, что она позволяла построить элегантный и мощный аппарат, объединяющий общую теорию относительности Эйнштейна и теорию электромагнитного поля Максвелла в единую и однородную концептуальную систему. Но как это предложение может согласовываться с тем очевидным фактом, что мы
Ответ, который в неявной форме содержится в работе Калуцы, и который позднее был выражен в явном виде и уточнен шведским математиком Оскаром Клейном в 1926 г., состоит в том, что
Чтобы получить более ясное представление о сути этого замечательного предложения, вернемся на минуту к примеру с Садовым шлангом. Представим себе, что на шланге черной краской нарисовано с малым шагом большое количество охватывающих его окружностей. Издалека шланг по-прежнему выглядит тонкой одномерной линией. Но, взглянув на него в бинокль, вы обнаружите свернутое измерение; после окраски найти его будет еще легче, чем раньше. Оно будет выглядеть так, как показано на рис. 8.2. Ясно видно, что поверхность шланга является двумерной, с одним крупным и протяженным измерением, а другим небольшим и имеющим форму окружности.
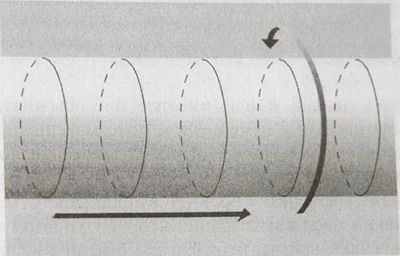 |
Рис. 8.2. Поверхность Садового шланга является двумерной. Одно измерение(идущее вдоль горизонтальной оси шланга), отмеченное прямой стрелкой, является длинным и протяженным. Другое измерение (окружность шланга), отмеченное круговой стрелкой, является маленьким и свернутым.
Калуца и Клейн предположили, что аналогичную структуру имеет и наша Вселенная, только в ней имеется три обычных, протяженных измерения и одно маленькое, циклическое; таким образом, общее число пространственных измерений равно четырем. Нарисовать предмет в пространстве с таким числом измерений непросто, поэтому для большей наглядности мы ограничились случаем двух протяженных и одного маленького циклического измерения. Мы изобразили это на рис. 8.3, где структура пространства последовательно увеличивается примерно так же, как в случае поверхности Садового шланга.
Самое нижнее изображение на рисунке показывает видимую структуру пространства — обычный окружающий нас мир в привычном масштабе расстояний, например, в метрах. Эти расстояния представлены самой редкой сеткой. На последующих изображениях структура пространства показана со все большим увеличением: мы фокусируем взгляд на все меньших областях, которые последовательно увеличиваем, чтобы сделать их видимыми. Сначала при переходе к меньшим расстояниям не происходит ничего особенного; на первых трех уровнях увеличения пространство сохраняет основные особенности своей структуры. Однако, по мере того как мы продолжаем наше путешествие вглубь микромира, на четвертом уровне увеличения на рис. 8.3 появляется новое, свернутое циклическое измерение, напоминающее круговые петли на ковре плотной вязки.
 |
Рис. 8.3. Как и на рис. 8.1, каждый последующий уровень представляет значительное увеличение пространственной структуры, показанной на предыдущем уровне. Видно, что наша Вселенная может иметь дополнительные измерения (как это показано на четвертом уровне увеличения), коль скоро они свернуты в столь малые пространственные образования, что не поддаются прямому наблюдению.
Калуца и Клейн предположили, что дополнительное циклическое измерение существует в
 |
Рис. 8.4. Линии сетки соответствуют обычным протяженным измерениям; кружками показаны новые малюсенькие свернутые измерения. Подобно круговым петелькам, образующим ворс ковра, эти кружки существуют в каждой точке протяженных измерений, однако чтобы не загромождать рисунок, мы нарисовали их только в узлах сетки.
Несмотря на очевидное сходство с Садовым шлангом, есть и несколько важных различий. Вселенная имеет три протяженных пространственных измерения (мы показали только два из них) по сравнению с одним таким измерением у Садового шланга. Однако еще важнее то, что на этом рисунке мы показали пространственную структуру самой
Итак, мы пришли к довольно удивительным выводам. Хотя мы наблюдаем только три протяженных пространственных измерения, рассуждения Калуцы и Клейна показывают, что это не исключает существования дополнительных, свернутых измерений, по крайней мере, если они достаточно малы. Вселенная вполне может иметь больше измерений, чем доступно нашему глазу.
Насколько малы должны быть эти измерения? Современная техника может обнаружить объекты, размер которых составляет одну миллиардную от одной миллиардной доли метра. Если дополнительное измерение свернуто до размера, который меньше этого значения, обнаружить его невозможно. В 1926 г. Клейн объединил первоначальное предположение Калуцы с некоторыми идеями бурно развивавшейся квантовой механики. Его расчеты показали, что дополнительное циклическое измерение по размерам сопоставимо с планковской длиной, что выходит далеко за рамки современных возможностей экспериментального изучения. С этого времени физики стали называть гипотезу о существовании дополнительных крошечных пространственных измерений
Наглядный пример Садового шланга и иллюстрации, приведенные на рис. 8.3, призваны прояснить то, почему наша Вселенная может иметь дополнительные пространственные измерения. Но даже специалистам, ведущим исследования в этой области, трудно наглядно представить Вселенную, имеющую более трех пространственных измерений. По этой причине физики, следуя примеру Эдвина Эббота[68], опубликовавшего в 1884 г. увлекательную книгу
Перейдем к еще более экстремальной точке зрения. Представим, что длина циклического измерения во вселенной Садового шланга очень мала, настолько мала, что ни вы, ни ваши собратья-обитатели шланга даже не подозреваете о существовании этого измерения. Напротив, вы и все живущие во вселенной Садового шланга считаете бесспорно очевидным следующий фундаментальный факт вашей жизни — вселенная имеет одно пространственное измерение. (Если бы вселенная Садового шланга породила своего муравьиного Эйнштейна, обитатели шланга могли бы сказать, что их вселенная имеет одно пространственное и одно временное измерение.) В действительности этот факт кажется им настолько самоочевидным, что обитатели шланга называют место, где они проживают,
Жизнь в Линляндии сильно отличается от той, к которой мы привыкли. Например, знакомые нам тела просто
Теперь представьте, что у вас есть по глазу на каждой стороне вашего тела. В отличие от глаз человека, которые могут вращаться в глазницах, чтобы иметь обзор в трех измерениях, ваши глаза, глаза линляндца, навсегда зафиксированы в одном положении, каждый из них направлен вдоль единственного измерения. Это
Мы можем попытаться дальше развивать наши представления о воображаемой жизни в Линляндии, но быстро осознаем, что она не слишком богата. Например, если по соседству с вами есть другой линляндец, представьте себе, как он будет выглядеть: вы увидите один его глаз, тот, который обращен к вам, но в отличие от глаза человека он будет выглядеть просто точкой. Глаза в Линляндии не имеют никаких индивидуальных особенностей и не выражают эмоций — для всего этого здесь просто нет места. Более того, вы навеки обречены видеть этот точечный глаз вашего соседа. Если вы захотите обойти его и исследовать ту часть Линляндии, которая лежит по другую сторону от его тела, вы будете очень разочарованы.
Несколько тысяч лет после пришествия бога в Линляндию, линляндец по имени Калуца К. Лин вселил некоторую надежду в сердца подавленных обитателей Линляндии. По божественному вдохновению или в полной тоске от многолетнего созерцания точечного глаза своего соседа он предположил, что Линляндия, в конце концов, может быть вовсе и не одномерной. Что, если, — теоретизировал он, — Линляндия на самом деле является двумерной, со вторым очень маленьким циклическим измерением, которое до сих пор не было открыто из-за его крошечного пространственного размера? Он продолжал рисовать картину совершенно новой жизни, которая начнется, если только удастся увеличить в размере это свернутое измерение — возможность, которую нельзя было отрицать согласно недавним работам его коллеги Линштейна. Калуца К. Лин описал вселенную, которая поразила вас и ваших сотоварищей и наполнила ваши сердца надеждой — вселенную, в которой линляндцы могут свободно обходить один другого, используя второе измерение: они перестанут быть рабами пространства. Вы поняли, что Калуца К.Лин описывает жизнь в «утолщенной» вселенной Садового шланга.
В действительности, если циклическое измерение разрастется, «раздув» Линляндию до вселенной Садового шланга, ваша жизнь изменится очень сильно. Возьмем, например, ваше тело. Поскольку вы линляндец, все, что находится между вашими глазами, составляет ваше тело. Следовательно, ваши глаза играют такую же роль для вашего линейного тела, как кожа для обычного человеческого тела: они образуют барьер между вашим телом и окружающим его миром. Врач в Линляндии может получить доступ к внутренностям вашего линейного тела только проколов их поверхность, — другими словами, «хирургическое вмешательство» в Линляндии осуществляется через глаза.
А теперь представим, что произойдет, если Линляндия действительно имеет секретное, скрытое измерение типа предложенного Калуцей К. Лином, и это измерение развернется до размера, поддающегося непосредственному наблюдению. Теперь другой линляндец может видеть ваше тело под углом и, следовательно, непосредственно сможет увидеть его внутренность, как показано на рис. 8.5.
 |
Рис. 8.5. Когда Линляндия расширится до размеров вселенной Садового шланга, один линляндец сможет заглянуть внутрь тела другого.
Используя это второе измерение, врачи смогут оперировать ваше тело, получая доступ непосредственно к вашим открытым внутренностям. Чудеса! Со временем, несомненно, у линляндцев разовьется покров, подобный кожному, защищающий вновь открывшиеся внутренности их тел от контакта с внешним миром. Более того, они несомненно эволюционируют в существ, имеющих не только длину, но и ширину: они станут плоскими существами, скользящими по двумерной вселенной Садового шланга, как показано на рис. 8.6.
 |
Рис. 8.6. Плоские двумерные существа, живущие во вселенной Садового шланга.
Если циклическое измерение станет очень большим, эта двумерная вселенная начнет очень походить на Флатляндию Эббота — воображаемый двумерный мир, который Эббот наделил богатой культурой и даже кастовой системой, основанной на геометрической форме тел обитателей. Если в Линляндии трудно представить себе
А теперь как рефрен: почему на этом надо остановиться? Двумерная вселенная сама может иметь свернутое измерение и, следовательно, втайне от нас быть трехмерной. Мы можем проиллюстрировать это рис. 8.4, представив, что существует только два протяженных пространственных измерения (хотя при первом описании этого рисунка мы считали, что плоская сетка представляет три протяженных измерения). Если циклическое измерение развернется, двумерные существа увидят, что они оказались в совершенно ином мире, в котором движения не ограничены направлениями влево-вправо и вперед-назад. Теперь эти существа могут двигаться и в третьем измерении — в направлении «вверх-вниз» вдоль круга. На самом деле, если третье измерение станет достаточно большим, это будет
И снова рефрен: почему на этом надо остановиться? Это приведет нас к представлениям Калуцы и Клейна: наша трехмерная Вселенная может иметь свернутое, четвертое пространственное измерение, о котором никто не подозревал. Если эта поразительная возможность или ее обобщение на случай многих свернутых измерений (мы вскоре рассмотрим его) истинны, и если эти свернутые измерения раскроются до макроскопического размера, то, как показывают приведенные выше примеры с меньшим числом измерений, жизнь в том виде, в котором мы ее знаем, изменится очень сильно.
Удивительно, однако, что даже если дополнительные измерения всегда будут оставаться в свернутом состоянии и будут малы, сам факт их существования ведет к глубоким последствиям.
Хотя высказанное Калуцей в 1919 г. предположение о том, что наша Вселенная может иметь недоступные нам непосредственно пространственные измерения, замечательно само по себе, его популярность связана с иными обстоятельствами. Эйнштейн сформулировал общую теорию относительности для привычного случая Вселенной с тремя пространственными и одним временным измерением. Однако математический формализм его теории можно непосредственно обобщить и выписать аналогичные уравнения для Вселенной с дополнительными пространственными измерениями. Калуца выполнил математический анализ и в явном виде выписал новые уравнения при «умеренном» предположении об одном дополнительном пространственном измерении.
Он обнаружил, что в этой пересмотренной формулировке уравнения, относящиеся к трем обычным измерениям, по существу совпадают с уравнениями Эйнштейна. Но благодаря тому, что он включил дополнительное пространственное измерение, Калуца, как и следовало ожидать, получил новые уравнения в дополнение к тем, которые первоначально вывел Эйнштейн. Изучив эти дополнительные уравнения, связанные с новым измерением, Калуца обнаружил нечто удивительное. Оказалось, что дополнительные уравнения представляют собой не что иное, как полученные Максвеллом в 1860-х гг. уравнения, описывающие электромагнитное взаимодействие! Добавив еще одно пространственное измерение, Калуца объединил теорию гравитации Эйнштейна с максвелловской теорией электромагнитного поля.
До появления гипотезы Калуцы гравитация и электромагнетизм рассматривались как два отдельных вида взаимодействия; ничто не указывало на то, что между ними может существовать какая-либо связь. Однако, дерзнув предположить, что наша Вселенная имеет дополнительное пространственное измерение, Калуца обнаружил, что в действительности они глубоко связаны. Его теория утверждает, что и гравитация, и магнетизм связаны с волнами в структуре пространства. Гравитация переносится волнами, распространяющимися в нашем обычном трехмерном пространстве, тогда как электромагнетизм переносится волнами, использующими новое, свернутое измерение.
Калуца послал свою статью Эйнштейну. Вначале Эйнштейн ей очень заинтересовался. 21 апреля 1919 г. он написал Калуце ответное письмо, в котором говорил, что ему никогда не приходило в голову, что подобное объединение может быть достигнуто «с помощью пятимерного [четыре пространственных измерения и одно временное] цилиндрического мира». Он также писал, что «на первый взгляд ваша идея нравится мне необычайно».[71] Однако спустя неделю Эйнштейн написал Калуце еще одно письмо, которое уже содержало изрядную долю скептицизма: «Я внимательно прочитал вашу статью и нахожу ее очень интересной. Я не вижу ничего, что позволило бы отрицать такую возможность. С другой стороны, я должен признать, что приведенные аргументы не выглядят достаточно убедительными».[72] Спустя более чем два года, 14 октября 1921 г., когда у Эйнштейна было достаточно времени, чтобы более полно усвоить новаторский подход, предложенный Калуцей, он снова пишет ему: «Я еще раз обдумал совет воздержаться от публикации вашей идеи об объединении гравитации и электромагнетизма, который я дал вам два года назад... Если вы хотите, я бы мог представить вашу статью в академии».[72] Так, с запозданием, Калуца получил одобрение мастера.
Хотя идея была прекрасной, последующий детальный анализ гипотезы Калуцы, дополненной Клейном, показал, что она находится в серьезном противоречии с экспериментальными данными. Простейшие попытки включить в теорию электрон приводили к предсказанию отношения его массы к заряду, которое существенно отличалось от измеренных значений. Поскольку не было видно способов разрешить эту проблему, многие физики потеряли интерес к идее Калуцы. Эйнштейн и ряд других ученых продолжали исследовать возможности использования дополнительных измерений, но тем не менее это направление вскоре оказалось на периферии теоретической физики.
В действительности, идея Калуцы намного опередила свое время. 1920-е гг. ознаменовались началом бурного роста теоретических и экспериментальных исследований, посвященных изучению основных законов микромира. Теоретики были поглощены разработкой структуры квантовой механики и квантовой теории поля. Экспериментаторы были заняты детальным изучением свойств атомов и поиском новых элементарных компонентов мироздания. Теория направляла эксперимент, а эксперимент подправлял теорию — так продолжалось около полувека, и, в конечном счете, это привело к разработке стандартной модели. Неудивительно, что в это бурное и продуктивное время предположения по поводу дополнительных измерений были на обочине исследований. В эпоху, когда физики открывали мощные методы квантовой механики, дававшие предсказания, которые могли быть проверены экспериментально, изучение возможности того, что Вселенная может иметь совершенно иные свойства на расстояниях, которые слишком малы, чтобы их можно было исследовать даже с помощью самой современной техники, вызывало мало интереса.
Но, рано или поздно, из машины выходит весь пар. К концу 1960-х — началу 1970-х гг. были разработаны теоретические основы стандартной модели. К концу 1970-х — началу 1980-х гг. многие ее предсказания получили экспериментальное подтверждение, и большинство специалистов по физике элементарных частиц пришло к выводу, что подтверждение оставшейся части этой теории является только вопросом времени. Хотя некоторые важные детали оставались невыясненными, многие думали, что на основные вопросы, касавшиеся сильного, слабого и электромагнитного взаимодействий, ответы уже получены.
Пришло время вернуться к величайшей проблеме: неразрешенному противоречию между общей теорией относительности и квантовой механикой. Успех в формулировке квантовых теорий трех взаимодействий, существующих в природе, вдохновил физиков на попытку разработать такую же теорию для гравитации. После того, как многочисленные гипотезы потерпели крах, сообщество физиков стало более восприимчивым к более радикальным подходам. Теория Калуцы-Клейна, оставленная умирать медленной смертью в конце 1920-х гг., была вновь воскрешена.
За шесть десятилетий, прошедших с момента первого появления гипотезы Калуцы, понимание физики значительно изменилось и углубилось. Квантовая механика была полностью сформулирована и получила экспериментальное подтверждение. Были открыты и, в значительной степени, объяснены сильное и слабое взаимодействия, которые в 1920-е гг. еще не были известны. Многие физики стали считать, что первоначальное предположение Калуцы потерпело неудачу из-за того, что он не знал об этих других взаимодействиях и был поэтому слишком
К середине 1970-х гг. развернулись интенсивные исследования, нацеленные на разработку теорий высших размерностей со многими свернутыми измерениями. На рис. 8.7 показан пример с двумя дополнительными измерениями, свернутыми в форму мяча, т.е. сферу.
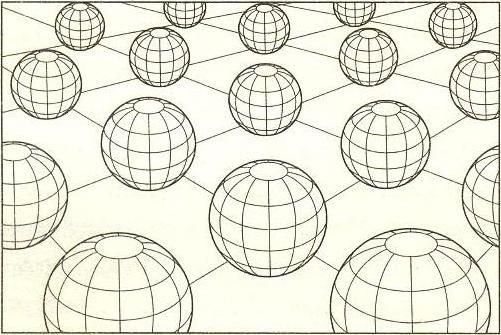 |
Рис. 8.7. Два дополнительных измерения, свернутые в сферу.
Как и в случае с одним циклическим измерением, эти дополнительные измерения присутствуют
 |
Рис. 8.8. Два дополнительных измерения, свернутые в баранку (тор).
Хотя это и выходит за пределы наших изобразительных возможностей, можно представить себе более сложные ситуации, в которых имеется три, четыре, пять и вообще произвольное число дополнительных пространственных измерений, свернутых в самые экзотические формы. Поскольку до сих пор не было получено экспериментального подтверждения существования всех этих измерений, существенным по-прежнему остается требование, чтобы их пространственный размер был меньше, чем самый малый масштаб длин, доступный современной технике.
Наиболее многообещающими из всех теорий с высшими размерностями были те, которые включали и суперсимметрию. Физики надеялись, что частичное сокращение наиболее интенсивных квантовых флуктуации, связанное с парами частиц-суперпартнеров, поможет смягчить противоречие между гравитацией и квантовой механикой. Для теорий, содержащих гравитацию, дополнительные измерения и суперсимметрию, они предложили название
Как и в случае с оригинальной гипотезой Калуцы, различные варианты многомерной супергравитации выглядят, на первый взгляд, многообещающе. Новые уравнения, появляющиеся в результате добавления новых измерений, поразительно напоминают уравнения, используемые для описания электромагнетизма, а также сильного и слабого взаимодействий. Однако более внимательный анализ показывает, что старые загадки никуда не исчезли. Еще более важно то, что катастрофические квантовые флуктуации пространства, возникающие на малых расстояниях, хотя и ослабляются суперсимметрией, но недостаточно для того, чтобы теория стала непротиворечивой. Физики также убедились, что трудно разработать единую, непротиворечивую теорию с высшими размерностями, объединяющую все свойства взаимодействий и материи.[73]
Постепенно становилось ясно, что хотя отдельные части объединенной теории начинают занимать свои места, однако ключевое звено, способное связать их в единое целое способом, не противоречащим квантовой механике, все еще отсутствовало. В 1984 г. это недостающее звено — теория струн — ярко вышло на сцену и заняло на ней центральное место.
К этому моменту вы должны были убедиться, что наша Вселенная
Таким было положение дел до появления теории струн. Эта теория разрешает центральное противоречие современной физики — несовместимость квантовой механики и общей теории относительности и унифицирует наше понимание всех фундаментальных компонент вещества и взаимодействий, существующих в природе. В дополнение к этим достижениям выясняется, что теория струн
Вот почему это так. Один из главных выводов квантовой механики состоит в том, что наша предсказательная способность принципиально ограничена утверждениями, что такой-то результат имеет такую-то вероятность. Хотя Эйнштейн испытывал неприязнь к современному пониманию квантовой теории (и вы можете согласиться с ним), факт остается фактом. Давайте принимать его таким, каков он есть. Как всем известно, значения вероятности всегда находятся между 0 и 1, или, если пользоваться процентами, между 0 и 100%. Как установили физики, первым признаком того, что квантовая механика перестает работать, является возникновение в расчетах «вероятностей», которые
С непоколебимым упорством физики искали и нашли причину появления этих неприемлемых результатов. Начнем объяснение с простого наблюдения. Если мы положим струну на двумерную поверхность (такую, как поверхность стола или Садового шланга), то число независимых направлений, в которых может колебаться струна, уменьшится до
Мы уделили такое внимание этому факту, относящемуся к колебаниям струн, потому что физики обнаружили: вычисления, дающие бессмысленные результаты, очень чувствительны к числу независимых направлений, в которых может колебаться струна. Отрицательные вероятности возникают из-за
Но остаются ли? Вспоминая об идее более чем полувековой давности, мы видим, что Калуца и Клейн оставили нам лазейку. Поскольку струны так малы, они могут колебаться не только в больших, протяженных измерениях, но и в крошечных свернутых. Таким образом, мы
Однако сразу же возникает ряд вопросов. Во-первых, почему теория струн требует именно девяти пространственных измерений для того, чтобы избежать бессмысленных значений вероятности? Это тот вопрос, на который, вероятно, труднее всего ответить без привлечения математического формализма теории струн. Прямой расчет с использованием аппарата теории струн приводит к этому результату, но никто не может дать интуитивного, не загроможденного техническими деталями объяснения, почему так происходит. Эрнест Резерфорд однажды сказал, что в действительности, если вы не можете объяснить результат на простом, не отягощенном специальными терминами языке, это значит, что вы не понимаете его по-настоящему. Слова Резерфорда не говорят, что ваш результат неверен, они говорят, что вы не полностью понимаете его происхождение, значение или следствия. Наверное, это справедливо по отношению к дополнительным измерениям в теории струн. (Воспользуемся возможностью упомянуть в скобках о центральном положении второй революции в теории суперструн, которую мы будем обсуждать в главе 12. Расчеты, лежащие в основе заключения о том, что имеется десять пространственно-временных измерений — девять пространственных и одно временное, оказались
Во-вторых, если уравнения теории струн (или, точнее, приближенные уравнения, которые мы будем обсуждать до главы 12) показывают, что Вселенная имеет девять пространственных измерений и одно временное, почему три пространственных измерения (и одно временное) являются развернутыми и протяженными, а все остальные — маленькими и свернутыми? Почему
В-третьих, если требуется несколько дополнительных измерений, не может ли быть так, что наряду с пространственными будут и дополнительные
Ситуация станет еще более загадочной, если вы подумаете о свернутых временных измерениях. Например, если крошечный муравей перемещается вдоль дополнительного пространственного измерения, свернутого наподобие круга, то, завершив очередной круг, он будет снова и снова оказываться в одном и том же месте. В этом мало удивительного, поскольку мы привыкли, что можем, если захотим, возвращаться в одно и то же место в пространстве столько раз, сколько нам нужно. Но если свернутое измерение является временным, перемещение вдоль него будет означать, что спустя какой-то промежуток мы будем оказываться в
Годы исследований, отсчет которых идет с первой статьи Калуцы, показали, что хотя размеры всех дополнительных измерений, предлагаемых физиками, должны быть слишком малы, чтобы мы могли наблюдать их непосредственно или с помощью имеющегося оборудования, эти измерения оказывают важное косвенное влияние на наблюдаемые физические явления. В теории струн эта связь между свойствами пространства на микроскопическом уровне и наблюдаемыми физическими явлениями видна особенно отчетливо.
Чтобы понять это, вспомним, что массы и заряды частиц определяются возможными модами резонансных колебаний струн. Представьте себе крошечную струну, которая движется и колеблется, и вы поймете, что моды резонансных колебаний подвержены влиянию со стороны окружающего пространства. Подумайте, например, о морских волнах. На бескрайних просторах океана отдельная изолированная волна может иметь любую форму и двигаться в любом направлении. Это очень похоже на колебания струны, движущейся по развернутым протяженным пространственным измерениям. Как указывалось в главе 6, такая струна в любой момент времени может колебаться в любом из протяженных измерений. Но когда морская волна проходит через более узкий участок, на форму волны будут влиять, например, глубина моря, расположение и форма скал, форма канала, по которому движется вода и т. п. Можно также представить себе органную трубу или валторну. Звук, который может воспроизводить каждый из этих инструментов, непосредственно зависит от резонансной моды колебаний воздуха, проходящего через них, а эта мода определяется формой и размерами каналов в инструменте, через которые движется поток воздуха. Свернутые пространственные измерения оказывают аналогичное влияние на возможные моды резонансных колебаний струны. Поскольку крошечные струны колеблются во всех пространственных измерениях, форма, в которую свернуты эти дополнительные пространственные измерения, а также форма их взаимного переплетения, сильно влияют и строго ограничивают возможные моды резонансных колебаний. Эти моды, в значительной степени определяемые геометрией дополнительных измерений, формируют набор свойств возможных частиц, наблюдаемых в привычных протяженных измерениях. Это означает, что
Это столь глубокий и важный момент, что мы повторим его еще раз. Согласно теории струн Вселенная состоит из крошечных струн. Моды резонансных колебаний этих струн определяют, на уровне микромира, массы и константы взаимодействия элементарных частиц. Теория струн также требует существования дополнительных измерений, которые должны быть свернуты до очень маленького размера, чтобы не было противоречия с тем фактом, что исследователям до сих пор не удалось их обнаружить. Но крошечные струны могут двигаться в крошечных пространствах. Когда струна перемещается, осциллируя по ходу своего движения, геометрическая форма дополнительных измерений играет решающую роль, определяя моды резонансных колебаний. Поскольку моды резонансных колебаний струн проявляются в виде масс и зарядов элементарных частиц, мы имеет право утверждать, что эти фундаментальные свойства Вселенной в значительной степени определяются размерами и формой дополнительных измерений. Этот результат представляет собой одно из наиболее глубоких следствий теории струн.
Поскольку дополнительные измерения оказывают столь глубокое влияние на фундаментальные физические свойства Вселенной, мы должны с неослабевающей энергией исследовать, как выглядят эти свернутые измерения.
Дополнительные пространственные измерения теории струн не могут быть свернуты произвольным образом: уравнения, следующие из теории струн, существенно ограничивает геометрическую форму, которую они могут принимать. В 1984 г. Филипп Канделас из университета штата Техас в г. Остине, Гари Горовиц и Эндрю Строминджер из университета штата Калифорния в г. Санта-Барбара, а также Эдвард Виттен показали, что этим условиям удовлетворяет один конкретный класс шестимерных геометрических объектов. Они носят название
Пример пространства Калаби-Яу показан на рис. 8.9.[76] Когда вы будете рассматривать этот рисунок, вы должны помнить, что ему присущи некоторые ограничения. Мы попытались представить шестимерное пространство на двумерном листе бумаги, что неизбежно привело к довольно существенным искажениям. Тем не менее, рисунок передает основные черты внешнего вида пространств Калаби-Яу.[77]
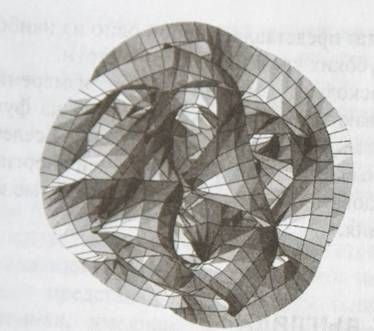 |
Рис. 8.9. Пример пространства Калаби-Яу.
На рис. 8.9 иллюстрируется всего лишь один из многих десятков тысяч возможных видов пространств Калаби-Яу, которые удовлетворяют строгим требованиям к дополнительным измерениям, вытекающим из теории струн. Хотя принадлежность к клубу, в который входят десятки тысяч членов, нельзя считать эксклюзивной особенностью, вы можете сравнить это число с бесконечным числом форм, которые возможны с чисто математической точки зрения; в этом смысле пространства Калаби-Яу действительно являются достаточно редкими.
Чтобы получить общую картину, вы должны теперь мысленно заменить каждую из сфер, показанных на рис. 8.7 и представляющих два свернутых измерения, пространством Калаби-Яу. Иначе говоря, как показано на рис. 8.10, в каждой точке нашего привычного трехмерного пространства согласно теории струн имеется шесть доселе неведомых измерений, тесно свернутых в одну из этих довольно причудливых форм.
 |
Рис. 8.10. Согласно теории струн Вселенная имеет дополнительные измерения, свернутые в пространство Калаби-Яу.
Эти измерения представляют собой неотъемлемую и вездесущую часть структуры пространства, они присутствуют повсюду. Например, если вы опишете рукой широкую дугу, ваша рука будет двигаться не только в трех развернутых измерениях, но и в этих свернутых. Конечно, поскольку эти свернутые измерения столь малы, ваша рука в своем движении пересечет их бесчисленное количество раз, снова и снова возвращаясь к исходной точке. Размеры этих измерений настолько малы, что в них не слишком много места для перемещения таких огромных объектов, как ваша рука, и все они «размазываются»: закончив движение руки, вы остаетесь в полном неведении о путешествии, которое она совершила сквозь свернутые измерения Калаби-Яу.
Это поразительная особенность теории струн. Но если у вас практичный ум, вы обязаны вернуться к обсуждению существенных и конкретных вопросов. Теперь, когда мы лучше понимаем, как выглядят дополнительные измерения, мы можем задать вопрос, какие физические свойства обязаны своим происхождением струнам, колеблющимся в этих измерениях, и как сравнить эти свойства с результатами экспериментальных наблюдений? В викторине под названием «теория струн» это вопрос на миллион долларов.
| © 2024 Библиотека RealLib.org (support [a t] reallib.org) |