"Математические чудеса и тайны" - читать интересную книгу автора (Гарднер Мартин)

Глава третья. ТОПОЛОГИЧЕСКИЕ ГОЛОВОЛОМКИ

В предыдущих главах мы рассматривали только такие фокусы, метод показа которых носит математический характер. Мы не занимались фокусами, в которых только конечный результат может быть объяснен при помощи математики. Если, например, показывающий, играя в карты, набирает нужное число взяток, заранее расположив карты в колоде соответствующим образом, то этот эффект можно считать математическим в том смысле, что произвольное расположение карт в колоде каким-то непостижимым образом стало упорядоченным, но мы такой фокус все же не будем называть математическим, поскольку показ его основан не на математике, а просто на незаметной подмене одной колоды другой.

Подобный подход мы применим и к отбору фокусов для настоящей главы. Очень многие «таинственные» фокусы можно назвать в широком смысле топологическими, так как при их показе как будто нарушаются элементарные топологические законы. Один из самых старинных фокусов такого рода известен под названием «соединенных колец»: шесть или более больших железных колец таинственным образом сцепляются и расцепляются — явление, кажущееся совершенно невозможным в силу свойств обычных замкнутых кривых линий. Другие фокусы, в которых кольца снимаются или надеваются на веревку или палку, оба конца которой зажаты в руках зрителя, можно было бы объяснить таинственными соединениями или разрывами цепи, поскольку зритель, держащий веревку, представляет собой замкнутую линию, через которую как-то проходит наше кольцо. Однако большинство таких фокусов основано на механических методах, небольшой ловкости рук или других «таинственных» приемах, ничего общего не имеющих с топологией.

Более близок к тому, что может быть названо топологической головоломкой, фокус, который известен под названием «падающее кольцо». Это цепочка колец, связанных друг с другом довольно странным образом. При надлежащих действиях верхнее кольцо как будто падает по цепи, пока, наконец, не оказывается странным образом соединенным с самым нижним кольцом. Этот фокус получается сам собой, и при его показе не возникает никаких затруднений, если не считать того, что кольца должны быть соединены так, чтобы они образовали некоторую сложную и довольно любопытную топологическую структуру.

«Падение» кольца в этом фокусе является лишь оптической иллюзией, объясняемой механически и не связанной с топологическими законами.

Весь материал этой главы будет включать в себя только фокусы, которые по методам показа могут рассматриваться как топологические. Так как топология занимается такими свойствами тел (предметов), которые не изменяются при непрерывных преобразованиях (растяжениях и сжатиях), при показе топологических фокусов (как и естественно ожидать) придется ограничиться почти исключительно таким гибким материалом, как бумага, ткани, нитки, бечевки и резиновые ленты.

Бумажные кольца

Хорошо всем известный «лист Мёбиуса», названный по имени Августа Фердинанда Мёбиуса, немецкого астронома и пионера-тополога, впервые описавшего эту поверхность, используется на протяжении последних 75 лет для многих фокусов. В одном из них показывающий вручает зрителю три больших бумажных кольца, каждое из которых получилось путем склеивания концов длинной бумажной ленты. Зритель разрезает ножницами первое кольцо вдоль ленты посередине, пока не вернется в исходную точку. В результате получаются два отдельных кольца. Разрезая таким же образом второе кольцо, он получает, к своему удивлению, не два кольца, а одно, которое вдвое длиннее исходного. Наконец, разрезая третье, он снова получает поразительный результат: два кольца, сцепленных друг с другом.

Результат этого фокуса зависит от того, как были сомкнуты концы ленты перед склейкой. Первое наше кольцо получилось путем простого соединения концов ленты без перекручивания. Второе кольцо (его называют листом Мёбиуса) получается при соединении концов ленты, перекрученной один раз на 180°. Одним из наиболее любопытных свойств этой поверхности, имеющей только одну сторону и один край, является то, что, разрезая ее вдоль посередине, мы получаем одно большое кольцо, если же разрезать его не посередине, а на расстоянии в одну треть ширины от края, то получается два кольца: одно большое и сцепленное с ним маленькое. Третье кольцо получилось при разрезании ленты, концы которой перекручивались перед склейкой дважды, т. е. на 360°.

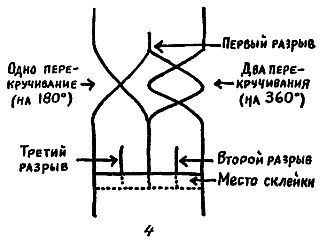
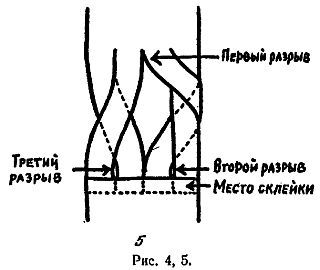
В другом варианте фокуса кольцо разрезается на два отдельных кольца, одно из которых при разрезании посередине превращается тоже в два отдельных кольца, а другое — в одно большое. Оригинальный метод приготовления кольца для такого фокуса показан на рис. 4, а его улучшение — на рис. 5. Для склеивания концов употребляется какой-нибудь быстросохнущий клей.

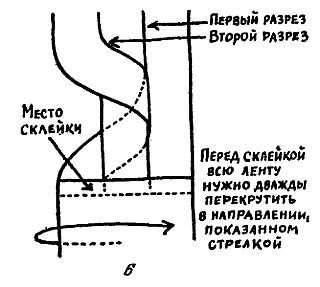
Способ приготовления бумажной ленты, при котором после двух разрезов получается цепочка из трех сцепленных колец, изображен на рис. 6.

Если изготовить кольцо так, как показано на рис. 7, то после первого разрывания (разрезания) получится большое кольцо, размер которого вдвое больше первоначального, а второе разрывание даст кольцо вчетверо длиннее исходного.

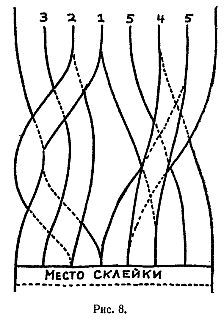
Другой вариант изображен на рис. 8, первое разрывание дает одно большое кольцо, а второе — два сцепленных.

Можно придумать и другие комбинации. Например, после разрывания кольца, изображенного на рис. 9, получаются два отдельных кольца. Разрывание одного из них дает цепочку из трех колец, разрывание другого — одно большое кольцо. Это последнее кольцо можно разрывать еще раз, причем получится еще большее кольцо.

Если трижды перекрученную ленту продеть сквозь перстень, склеить концы, а затем разрезать или разорвать вдоль посередине, то получится одно большое кольцо с узлом, завязанным вокруг перстня.