"Моделирование рассуждений. Опыт анализа мыслительных актов" - читать интересную книгу автора (Поспелов Дмитрий Александрович)

Нечеткая силлогистика

Силлогистика Аристотеля совсем недавно вновь стала объектом пристального внимания исследователей. Идеи нечетких рассуждений оказались перенесенными на модусы и фигуры, казавшиеся венцом достоверных рассуждений. Прежде чем изложить эти идеи, опишем одну историю, которую можно было бы назвать «Силлогизм бабушки».

«Жара уже спадала, когда Сумбурук и Твидл приехали в один маленький городок – кажется, где-то на юге Франции. Возле автостоянки был бар. Они оставили машину, договорились встретиться в баре вечером и разошлись кто куда. Сумбурук пошел бродить по незнакомым улицам, а Твидл сразу направился в бар: он всегда больше предпочитал сидеть, чем ходить.

К вечеру в бар, помахивая бамбуковой тросточкой, вошел Сумбурук. На голове у него был роскошный блестящий цилиндр.

– Вырядился, прямо как Макс Линдер. Только полосатых панталон не хватает, – сказал Твидл, когда Сумбурук приблизился к нему. – Красивая тросточка. И цилиндр, кстати, тебе идет.

– Хочешь, можешь тоже купить. Они продаются на каждом углу. А кто в цилиндре… – Сумбурук слегка, кончиками пальцев коснувшись цилиндра, сделал незаметный жест, и тросточка в другой его руке завертелась, как пропеллер. – Те, с тросточкой, я заметил, почти всегда, – закончил он и присел за стойку, собираясь заказать себе абсент. Но не успел он это сделать, как с удивлением обнаружил, что рюмка крепкого зеленоватого напитка уже стоит перед ним.

– Не удивляйся, – заметил Твидл. Он (Твидл кивнул на бармена) увидел, как ты вертел тросточкой, вот и все. Держу пари, здесь все, кто с тросточкой, пьют исключительно абсент. По крайней мере, за три часа, пока я здесь, он ни разу не ошибся. Да и то сказать, – Твидл еще раз оглядел Сумбурука, – с таким цилиндром и тросточкой можно разве в этом городе пить что-нибудь кроме абсента?

Сумбурук сделал глоток и на секунду задумался.

– Я, кажется, могу дать ему дельный совет, – сказал он и показал незаметно на бармена. Сумбурук щелкнул пальцами, и бармен поглядел на него.

– А тем, кто в цилиндре, вы тоже сразу наливаете абсент?

– Да, если в руках еще и тросточка, – ответил бармен.

– Но в этом городе все, кто в цилиндре, ходят с тросточкой, разве нет?

– Почти все, – поправил бармен. – Вам налить что-нибудь другое? И он с подозрением посмотрел на цилиндр Сумбурука

– Все в порядке, – успокоил его Сумбурук. Просто мой вам совет: тому, кто в цилиндре, с тросточкой он или без тросточки, можете, не спрашивая, тоже смело наливать абсент – не ошибетесь никогда.

– Не ошибусь? – переспросил бармен. – Никогда? Вы уверены?

– Ну, почти никогда. Еще Аристотель говорил, если почти все, кто носит цилиндр, ходят с тросточкой, и почти все, кто ходит с тросточкой, пьют только абсент, то почти все, кто носит цилиндр, тоже пьют только абсент. Согласны? – спросил Сумбурук. Он когда-то изучал логику и немного гордился этим[8].

– Вы не правы, – к удивлению друзей вежливо, но твердо возразил бармен. – Еще моя покойная бабушка, помню, любила повторять, если почти все, кто носит цилиндр, ходят с тросточкой, и вместе с тем почти все, кто ходит с тросточкой, пьют только абсент, то наверняка можно сказать только одно: из тех, кто носит цилиндр, многие пьют только абсент. Многие – да, согласен. А сказать "почти все" – это неверно.

Сумбурук никогда не был формалистом, – скорее, напротив. Но тут, немного задетый, он (с кем не бывает!) задал вопрос, который вряд ли пришел бы в голову Максу Линдеру:

– А что значит "многие"?

– Да-да, – поддержал его Твидл, – "многие" это что, больше 30 %, больше 50 % или, может, больше 90 %?

– Ну, 90 % это вряд ли, – сказал бармен, слегка ошарашенный таким обилием неизвестно откуда взявшихся цифр. – Во всяком случае "многие" это не то же самое, что "почти все". В нашем городе вкусы меняются медленно, и поверьте, я на собственном опыте знаю: моя бабушка была права.

– По всему выходит, что ваша бабушка умнее Аристотеля, – заметил Твидл.

Бармен пожал плечами.

– Я, простите, ничего не знаю о человеке по имени Аристотель. Он, наверное, грек, а я наполовину француз. Но могу сказать одно, – тут он взял бутылку абсента и налил нашим друзьям еще по рюмке, – моя бабушка была очень умная и добропорядочная женщина».

Постараемся разобраться в силлогизме бабушки. Введем ряд обозначений:

а – количество людей, которые ходят в цилиндре;

b – количество людей, которые ходят с тросточкой;

с – количество людей, которые пьют только абсент;

Р(b/а) – доля тех, кто ходит с тросточкой среди тех, кто носит цилиндр;

Р(c/b) – доля тех, кто пьет только абсент, среди тех, кто ходит с тросточкой;

Р(c/a) – доля тех, кто пьет только абсент, среди тех, кто ходит в цилиндре;

Р(а) – доля тех жителей города, которые ходят в цилиндре, от всех жителей города;

Р(b) – доля тех, кто ходит с тросточкой, от всех жителей города;

Р(c) – доля тех, кто пьет только абсент, от всех жителей города.

Получение всей этой информации требует некоторого статистического обследования жителей города и их привычек. Результаты такого обследования могут быть сведены в таблицу сопряженности (табл. 5).

Таблица 5

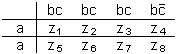В этой таблице z₃, например, доля жителей торода, которые ходят в цилиндре и с тросточкой, но не пьют абсента. Аналогичным образом интерпретируются и остальные ее элементы. Значения z₁, удовлетворяют ряду соотношений.

1. z₁+z₂+z₃+z₄+z₅+z₆+z₇+z₈=1.

Это соотношение вытекает из нормировки, так как z_i – доли.

2. Восемь ограничений вида z_i?0, вытекающие из смысла z_i, i=1,2,…,8.

3. Предположим, что в городе множества жителей, которые носят цилиндр, ходят с тросточкой и пьют только абсент, не являются пустыми. Это означает, что должны выполняться следующие неравенства:

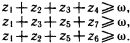Значение ? выбрано так, чтобы все эти три неравенства были справедливы.

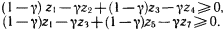4. Еще два неравенства связаны с тем, что величины Р(b/а) и Р(c/b), входящие в посылку силлогизма бабушки, должны удовлетворять ограничениям P(b/a)?? и P(c/b)??, где ? подобрано таким образом, чтобы оба неравенства выполнялись. Если условные частоты выразить через элементы таблицы сопряженности, то можно получить еще два неравенства:

В этих ограничениях два параметра: ? и ?. Варьируя их, можно вводить различные нечеткие квантификаторы в силлогизм типа силлогизма бабушки или силлогизма Сумбурука.

Дадим некоторые необходимые пояснения к приведенной системе. Посылки силлогизма бабушки, как его сформулировал бармен, звучат так: «Из тех, кто носит цилиндр, почти все ходят с тросточкой» И «Из тех, кто ходит с тросточкой, почти все пьют только абсент». Заглавная буква И отделяет один член посылки от другого. Первый член посылки говорит о том, что P(b/a) есть нечеткий квантификатор «почти все», а второй член посылки содержит аналогичное утверждение относительно P(c/b). Если считать, что нечеткому квантификатору «почти все» на лингвистической шкале соответствует некоторый отрезок, то он имеет вид [?,1], где ?gt;0. Именно в этом смысл двух последних неравенств. В силлогизме бабушки дается оценка нечеткого квантификатора, соответствующего Р(с/а). Бабушка считает, что Р(с/а) соответствует квантификатор «многие». Сумбурук же считает, что Р(с/а) соответствует квантификатор «почти все». Значит, бабушка предполагает, что Р(с/а) на лингвистической шкале соответствует полуинтервал [?,?] и ?gt;0, а Сумбурук уверен, что это отрезок [?,1]. В этом и состоит их несогласие.

Их спор происходит в условиях некоторого «контекста». Этот контекст определяется величинами Р(а), Р(b) и Р(с), характерными для данного городка. В наших ограничениях контекст определяется параметром ?.

Силлогизмы бабушки и Сумбурука – это формальный вывод вида АВ. Здесь А – посылка силлогизма, общая для бабушки и Сумбурука, а В – заключение, которое у бабушки имеет вид «Р(с/а) есть нечеткий квантификатор «многие»», а у Сумбурука – вид «Р/(c/a) есть нечеткий квантификатор «почти все»». Вывод: силлогизм происходит в условиях контекстных ограничений, характеризуемых параметром ?.

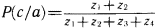Как разрешить спор? Выход один. Надо задать значения ?, ? и ? и свести проблему к решению типовой задачи линейного целочисленного программирования, которая формулируется следующим образом. Найти целочисленные значения z_i?0 (i=1,2,…,8), такие, что удовлетворяются шесть вышеприведенных неравенств, и такие, что минимум функции

достигает своего максимума.

Если задача решена и минимум Р(с/а) есть ? и этот минимум удовлетворяет неравенству ???, то верен силлогизм бабушки. А если ???lt;?, то верен силлогизм Сумбурука. Если же ?lt;?, то и бабушка, и Сумбурук ошиблись. Их силлогизмы будут ложными.

Значит, все зависит от того, как определены ?, ? и ?. Пусть для определения этих значений мы опросили четырех людей Ч₁, Ч₂, Ч₃ и Ч₄. Их ответы сведены в табл. 6.

Таблица 6

Интерпретация чисел в таблице следующая. Опрашиваемый считает, что можно говорить «почти все», когда явление это встречается не реже, чем в 95 случаях из 100. Аналогично интерпретируются и остальные элементы таблицы. В первом столбце стоят значения ?, во втором ?, а в третьем ?. Каждая строка может быть использована для решения задачи линейного программирования, которую мы сформулировали. Если решить возникающие четыре задачи, то выяснится, что силлогизм бабушки оказывается истинным во всех случаях, кроме третьего. В третьем случае прав Сумбурук, а бабушка ошибается.

Из сказанного ясно, что при исследовании нечетких силлогизмов (или D-cиллогизмов, как их принято называть) необходимо анализировать области в пространстве параметров ?, ?, ?, в которых будут истинны или ложны те или иные силлогизмы. В частности, для силлогизма бабушки доказывается следующее утверждение, которое естественно было бы назвать Теоремой бармена: «Силлогизм бабушки истинен только в тех точках параметрического пространства, в которых выполняется соотношение ??max[0,2?1/?, 1?(1??)(?+1/?)]». Но, наверное, ни бармен, ни Сумбурук не смогли бы так четко сформулировать нужный для разрешения их спора результат.

Рассуждая о споре в баре, мы незаметно сформулировали метод формального поиска оценок нечетких квантификаторов в схемах рассуждений. Ведь если вернуться к схемам предшествующего раздела, то становится ясным, что метод решения силлогизма бабушки вполне пригоден для поиска ₂ в заключениях этих схем.