"Дядюшка Петрос и проблема Гольдбаха" - читать интересную книгу автора (Доксиадис Апостолос)

2

Приехав на летние каникулы в Грецию, я на второй день отправился в Экали. Не желая застать дядю врасплох, я предварительно списался с ним и назначил эту встречу. Если продолжить юридическую аналогию, я дал ему достаточно времени на подготовку защитительной речи.

Прибыл я в назначенное время, и мы сели в саду.

– Итак, любимейший из племянников (тогда он меня впервые так назвал), какие новости привез ты мне из Нового Света?

Если он думал, что я позволю ему притворяться, будто к любящему дяде приехал почтительный племянник, то он ошибся.

– Итак, дядя, – сказал я воинственно, – через год я получаю степень и уже готовлюсь поступать в аспирантуру. Твоя интрига не удалась. Нравится тебе это или нет, а я буду математиком.

Он пожал плечами и воздел руки к небесам, принимая неизбежное.

– Кому суждено утонуть, не умрет в своей постели, – выразительно произнес он популярную греческую пословицу. – Ты отцу сказал? Он был рад?

– Откуда такой внезапный интерес к мнению моего отца? – рявкнул я. – Разве это он заключил со мной так называемый уговор? Это у него была извращенная идея заставить меня доказать свою пригодность, решив проблему Гольдбаха? Или ты из чувства долга за поддержку, которую он тебе все эти годы оказывал, отплатил ему тем, что щелкнул по носу его выскочку-сына?

Дядя Петрос перенес все эти удары ниже пояса с полным спокойствием.

– Я понимаю, что ты рассержен, – сказал он. – Но ты должен попытаться понять. Хотя способ я выбрал сомнительный, мотивы у меня были чисты, как свежий снег.

Я саркастически рассмеялся:

– Ничего себе «чисты»! Чтобы твоя ошибка определила мою жизнь!

Он вздохнул:

– Ты располагаешь временем?

– Сколько тебе будет нужно.

– Тебе удобно сидеть?

– Вполне.

– Тогда слушай мою историю. Слушай и суди сам.

История Петроса Папахристоса

Сейчас, когда я это пишу, я уже не могу вспомнить точных слов и выражений, которые использовал мой дядя в тот летний день много лет назад. Я решил изложить его рассказ в третьем лице ради полноты и связности. Там, где меня подводила память, я пользовался его сохранившейся перепиской с семьей и коллегами, а также толстыми томами его дневников в кожаных переплетах, куда он записывал ход своих исследований.

Петрос Папахристос родился в Афинах в ноябре 1895 года. Раннее детство он провел почти одиноко – перворожденный сын промышленника, добившегося положения своим трудом, и домашней хозяйки, чьей единственной заботой был ее супруг.

Великая любовь часто рождается из одиночества, и таков был роман длиною в жизнь у моего дяди с числами. Он рано открыл в себе способности к счету, и эти способности благодаря отсутствию отвлекающих факторов довольно быстро переросли в страсть. Еще в самом раннем детстве он заполнял пустые часы, высчитывая сложные суммы, в основном мысленно. Когда с появлением двух младших братьев в доме стало веселее, он уже был так увлечен своей страстью, что его не могли отвлечь никакие изменения в жизни семьи.

Школа, где учился Петрос, – религиозное учреждение, основанное французскими иезуитами, поддерживало блестящие традиции ордена в математике. Брат Николай, его первый учитель, немедленно обнаружил наклонности мальчика и взял его под свое крыло. Под его руководством ребенок начал изучать материал, далеко выходивший за возможности его одноклассников. Как большинство математиков-иезуитов, брат Николай специализировался в классической геометрии (старомодной уже в те годы). Он посвящал свое время составлению задач – часто изящных и почти всегда чудовищно трудных, но не представляющих глубокого математического интереса. Петрос решал и их, и любые другие задачи, которые учитель выкапывал из иезуитских математических книг, с удивительной легкостью.

Но особой его страстью с самого начала была теория чисел – область, в которой у братьев особых знаний не было. Его несомненный талант в сочетании с постоянными тренировками с малых лет давал почти невероятные результаты. Когда Петрос в возрасте одиннадцати лет узнал, что любое натуральное число можно выразить в виде суммы четырех квадратов, он поражал добрых наставников, делая это разложение для любого числа, которое они ему задавали, задумавшись всего на несколько секунд.

– А 99, Пьер? – спрашивали они.

– 99 равно 8² плюс 5² плюс 3² плюс 1², – отвечал он.

– А 290?

– 290 равно 12² плюс 9² плюс 7² плюс 4².

– Но как тебе удается это так быстро делать? Петрос описал им метод, который ему казался очевидным, но его учителям трудно было его понять и невозможно применить без бумаги, карандаша и наличия времени. Процедура основывалась на логических скачках, обходящих промежуточные этапы вычисления – явное свидетельство того, что математическая интуиция у мальчика развилась редкая.

Когда иезуиты более или менее научили Петроса всему, что знали сами, оказалось, что они не в состоянии ответить на постоянный поток математических вопросов своего одаренного ученика. Петросу к тому времени было пятнадцать лет. И вот тогда директор школы пошел к его отцу. Папахристос-père, быть может, не уделял детям много времени, но свой долг в том, что касалось греческой православной церкви, он знал. Своего старшего сына он записал в школу к этим схизматикам-иностранцам потому, что это было престижно в той элитной среде, куда он мечтал попасть. Однако, услышав предложение директора отправить его сына в монастырь во Франции для дальнейшего развития математического таланта, он незамедлительно подумал о прозелитизме.

«Эти проклятые паписты хотят наложить лапы на моего сына», – понял он.

Но старший Папахристос, несмотря на отсутствие высшего образования, глупцом никак не был. Зная по собственному опыту, что человек лучше всего преуспевает там, где у него есть природный дар, он совершенно не желал ставить сыну препятствия на его естественном пути. Расспросив нужных людей в нужных кругах, он выяснил, что в Германии есть великий математик греческого православного вероисповедания, знаменитый Константин Каратеодори. Отец Петроса немедленно написал к нему с просьбой о встрече.

Отец и сын поехали в Берлин, где Каратеодори принял их в своем университетском кабинете, одетый, как банкир. После короткого разговора с отцом профессор попросил оставить его наедине с сыном. Он подвел Петроса к доске, дал ему мел и стал спрашивать. Петрос брал интегралы, считал ряды и доказывал утверждения, которые ему предлагались. Когда же знаменитый профессор закончил экзамен, мальчик рассказал о своих собственных открытиях: изощренные геометрические построения, сложные алгебраические преобразования и, в частности, наблюдения над свойствами целых чисел. Одним из них было такое: «Каждое четное число, большее 2, может быть записано в виде суммы двух простых чисел».

– Ну, это вы не умеете доказывать, – сказал знаменитый математик.

– Пока нет, – ответил Петрос, – хотя я уверен, что это общий принцип. Я его проверил до 10000.

А что вы знаете о распределении простых чисел? – спросил Каратеодори. – Можете указать способ определить, сколько существует простых чисел, меньших заданного n?

– Не могу, – ответил Петрос, – но когда n стремится к бесконечности, это число очень близко к отношению n и его натурального логарифма. Каратеодори ахнул.

– Вы это где-то прочитали!

– Нет, господин профессор, это просто экстраполяция из моих таблиц. К тому же в нашей школе есть книги только по геометрии.

Строгое выражение лица профессора сменилось сияющей улыбкой. Он позвал отца Петроса и сообщил, что держать его сына еще два года в школе было бы просто потерей времени. Препятствовать мальчику с таким необыкновенным даром получить лучшее, что предлагает математическое образование, равносильно, как он сказал, «преступному небрежению». Каратеодори немедленно организует прием Петроса в университет – если, конечно, его опекун согласен.

У бедного дедушки не было выбора. Он никак не хотел совершать преступление, тем более против своего первенца.

Прием был организован, и через несколько месяцев Петрос вернулся в Берлин и поселился в семье делового партнера своего отца, в Шарлоттенбурге.

В те месяцы, которые оставались до начала учебного года, старшая дочь хозяина дома, восемнадцатилетняя Изольда, решила помочь молодому иностранному гостю в изучении немецкого языка. Дело было летом, и уроки проходили в укромных уголках сада. Когда стало холоднее, уроки, как вспомнил с мечтательной улыбкой дядя Петрос, «были перенесены в постель».

Изольда была первой и (если верить рассказу) единственной любовью моего дяди. Роман их был краток и хранился в полной тайне. Свидания происходили нерегулярно и в самых неожиданных местах – в полдень, в полночь и на рассвете, в кустах и на чердаке, всегда и везде, где открывалась возможность остаться незамеченными: если отец узнает, как предупреждала девушка, он Петроса повесит за ноги.

На какое-то время Петрос полностью потерял голову от любви. Он до такой степени стал безразличен ко всему, кроме своей возлюбленной, что Каратеодори начал задумываться, правильно ли он оценил способности мальчика. Но после недолгих месяцев мучительного счастья («слишком, увы, недолгих», сказал дядя со вздохом), Изольда покинула отчий дом и объятия юного любовника, чтобы выйти за некоего бравого прусского артиллерийского лейтенанта.

Конечно, сердце Петроса было разбито.

Если детская страсть к числам частично служила компенсацией за недостаток родительской любви, то погружение в стихию высшей математики в Берлинском университете стало еще более полным возмещением потери любимой. Чем глубже погружался Петрос в бескрайний океан абстрактных понятий и таинственных символов, тем дальше уходил от мучительно сладких воспоминаний о «милой Изольде». Вышло так, что она, отсутствуя, «оказалась куда полезнее» (слова Петроса). Когда они впервые легли вместе на ее постель (когда она впервые затащила его в свою постель, чтобы быть точным), она тихонько мурлыкала ему в ухо, что привлекла ее к нему его репутация вундеркинда, маленького гения. Чтобы вновь завоевать ее сердце, Петрос решил теперь, что полумер будет мало. Сейчас, в более зрелом возрасте, он должен поразить ее потрясающими интеллектуальными достижениями, стать Великим Математиком – никак не меньше.

Но как может человек стать Великим Математиком? А просто: решить Великую Математическую Проблему!

– Какая сейчас самая трудная проблема в математике, господин профессор? – спросил он у Каратеодори при очередной встрече, пытаясь изобразить чисто академическое любопытство.

– Я бы назвал три главные, – ответил мудрец после секундного размышления. – Гипотеза Римана, последняя теорема Ферма и последняя по порядку, но не по значению проблема Гольдбаха – утверждение, что любое четное число представляется в виде суммы двух простых – одна из величайших нерешенных проблем теории чисел.

Еще никак не твердое решение, а всего лишь первое зернышко мечты, что когда-нибудь он решит проблему Гольдбаха, после краткого разговора с Каратеодори пустило корни в сердце Петроса. Тот факт, что это наблюдение он сам сделал еще задолго до того, как услышал о Гольдбахе или Эйлере, делал для него задачу еще дороже. С самого начала его потянула к себе эта формулировка. Сочетание внешней простоты и прославленной трудности явно показывало, что здесь заключена глубокая истина.

Но в тот момент Каратеодори не дал Петросу времени на мечтания.

– Прежде чем вы сможете плодотворно заняться самостоятельными исследованиями, – сказал он тоном, не допускающим возражений, – вы должны приобрести мощный арсенал. Вы должны в совершенстве овладеть всеми инструментами современной математики из анализа, комплексного анализа, топологии и алгебры.

Даже от молодого человека с таким экстраординарным талантом это овладение требовало времени и неослабного внимания.

Когда Петрос получил диплом, Каратеодори дал ему в качестве темы для диссертации задачу из теории дифференциальных уравнений. Петрос удивил учителя, сделав работу меньше чем за год и с потрясающим успехом. Метод решения некоторого вида уравнений, который он предложил в своей диссертации (с тех пор «метод Папахристоса»), принес Петросу немедленное признание из-за полезности при решении определенного класса физических задач. Но – цитирую Петроса – «никакого математического интереса в этом не было, просто расчеты для бакалейной лавки».

Докторскую степень Петрос получил в 1916 году. Сразу после этого его отец, тревожась из-за неминуемого вступления Греции в свалку мировой войны, устроил его на время в нейтральной Швейцарии. В Цюрихе, став наконец хозяином собственной судьбы, Петрос вернулся к своей первой и постоянной любви: к Числам.

Он получил курс в университете, посещал лекции и семинары, а оставшееся время проводил в библиотеке, поглощая книги и листая журналы. Вскоре ему стало ясно, что для того чтобы добраться до передовых границ знаний, придется попутешествовать. Работы мирового класса по теории чисел делали в это время три человека: англичане Г.Х. Харди и Дж. И. Литлвуд и необычайно одаренный гений-индиец Сриниваса Рамануджан. Все трое работали в кембриджском Тринити-колледже.

Война разделила Европу на части, практически отрезав Англию от материка проливами, где патрулировали немецкие подводные лодки. Но горячее желание Петроса в сочетании с его полным безразличием к опасности, а также более чем достаточные средства вскоре помогли ему достигнуть цели.

«В Англию я прибыл все еще начинающим, – сказал он мне, – но через три года покинул ее специалистом по теории чисел».

Конечно, эти три года в Кембридже были существенной подготовкой к последующим долгим и тяжелым годам. Он не имел официальной академической должности, но его – точнее, отцовское – финансовое положение давало ему возможность позволить себе роскошь обойтись без таковой. Он поселился в небольшом пансионе рядом с Бишоп-отелем, где в это время жил Сриниваса Рамануджан. Вскоре они подружились и вместе стали ходить на лекции Г.Х. Харди.

Харди воплощал собой образец современного ученого-математика. Истинный мастер своего искусства, он подходил к теории чисел с блестящей ясностью, используя самые изощренные математические методы для атаки на ее центральные проблемы, многие из которых, подобно проблеме Гольдбаха, отличались обманчивой внешней простотой. На его лекциях Петрос изучал методы, которые потом окажутся необходимыми для его работы, и начал вырабатывать глубокую математическую интуицию, необходимую для исследований на переднем крае. Он усваивал быстро и вскоре начал составлять схему лабиринта, в который ему было уготовано судьбой войти.

И все же, хотя в его развитии как математика ключевую роль играл Харди, вдохновляло его общение с Рамануджаном.

«О, это был совершенно уникальный феномен, – сказал Петрос со вздохом. – Как говорил Харди, в смысле математических способностей Рамануджан был абсолютной вершиной. Он был сделан из того же теста, что Архимед, Ньютон и Гаусс – можно даже предположить, что он превосходил их. Однако почти полное отсутствие формального математического образования в годы становления обрекло его на реализацию лишь очень малой доли его гения.

Смотреть, как Рамануджан занимается математикой, очень не способствовало самомнению. Благоговение и изумление – единственная реакция на невероятные способности этого человека вспышкой интуиции постигать самые непостижимые формулы и понятия. (Ультрарационалист Харди из себя выходил, когда Рамануджан часто заявлял, будто это ему открывает во сне его любимая индуистская богиня Намакири.) Нельзя было не задуматься: если бы крайняя нищета, в которой родился Рамануджан, не лишила его образования, которое получает средний хорошо накормленный западный школьник, каких высот мог бы он достичь?

Однажды Петрос в разговоре с ним робко коснулся проблемы Гольдбаха. Он намеренно был осторожен, чтобы не дай Бог не пробудить интереса к задаче.

Ответ Рамануджана его неприятно удивил: Знаете, у меня есть предчувствие, что это может быть неверно для некоторых очень больших чисел.

Петрос был как громом поражен. Может ли такое быть? Раз это говорит Рамануджан, то отмахнуться от такого замечания нельзя. При первой возможности Петрос подошел к Харди после лекции и повторил ему слова Рамануджана, стараясь, чтобы они прозвучали достаточно безразлично. Харди хитровато улыбнулся.

– Старина Рамануджан известен своими чудесными «предчувствиями», – сказал он, – и интуиция у него феноменальная. Все же он в отличие от Его Святейшества Папы не обладает непогрешимостью.

Тут Харди пристально посмотрел на Петроса, и в его глазах мелькнула легкая ирония.

– А скажите, дорогой коллега, откуда вдруг такой интерес к проблеме Гольдбаха?

Петрос промямлил какие-то банальности насчет «общего интереса к этому вопросу» и спросил как можно более невинным тоном:

– А кто-нибудь здесь над ней работает?

– Вы хотите сказать, пытается доказать? – спросил Харди. – Нет, конечно! Попытка решить эту задачу в лоб – чистое безумие!

Такое предупреждение Петроса не отпугнуло; напротив, оно показало ему нужное направление. Смысл слов Харди был совершенно ясен: прямой, так называемый элементарный подход к проблеме обречен на провал. Правильный путь лежит через окольный «аналитический» метод, который после недавнего большого успеха французских математиков Адамара и Валле-Пуссена, стал в теории чисел très à la mode [12]. И вскоре Петрос с головой ушел в его изучение.

В Кембридже у него был период, еще до того, как он принял окончательное решение о труде своей жизни, когда Петрос всерьез рассматривал возможность посвятить свои силы совершенно другой проблеме. Она возникла в результате его неожиданного попадания во внутренний круг Харди – Литлвуда – Рамануджана.

В годы войны Дж. И. Литлвуд не много времени проводил в университете. Он порой появлялся на лекции или на заседании и снова исчезал Бог знает куда, а его деятельность была окутана покровом таинственности. Петросу еще только предстояло с ним познакомиться, и поэтому он был крайне удивлен, когда в начале 1917 года Литлвуд остановил его рядом с пансионом.

– Вы – Петрос Папахристос из Берлина? – спросил Литлвуд после рукопожатия и осторожной улыбки. – Ученик Константина Каратеодори?

– Да, это я, – ответил слегка озадаченный Петрос. Литлвуд держался несколько напряженно, когда стал объяснять: он сейчас руководит группой, которая ведет исследования по баллистике для Королевской артиллерии. Военная разведка недавно оповестила их о том, что высокая точность огня противника на западном фронте объясняется применением нового способа расчетов, называемого «метод Папахристоса».

– Я уверен, что вы не откажетесь поделиться вашим открытием с правительством Его Величества, старина, – заключил Литлвуд. – В конце концов Греция наш союзник.

Петрос сперва пришел в отчаяние, испугавшись, что его заставят тратить драгоценное время на задачи, которые ему абсолютно не интересны. Но в этом, как выяснилось, не было необходимости, В тексте его диссертации, который у него, к счастью, был с собой, оказались все результаты, потребные Королевской артиллерии. Литлвуду было вдвойне приятно, поскольку метод Папахристоса не только оказался полезен для воюющей армии, но и сильно облегчил нагрузку самого Литлвуда, освобождая ему время для занятий математикой.

И вышло так, что ранний результат Петроса в области дифференциальных уравнений не только не увел его в сторону, но и открыл ему путь в одно из самых известных содружеств в истории математики. Литлвуд был рад узнать, что сердце его талантливого греческого коллеги принадлежит, как и его собственное, теории чисел, и вскоре пригласил Петроса присоединиться к нему при визите к Харди. Они втроем часами говорили о математике. В течение этой и всех последующих встреч и Литлвуд, и Петрос всячески избегали любых упоминаний о том, что свело их вместе: Харди был фанатичным пацифистом и резко возражал против использования научных открытий для войны.

После заключения мира, когда Литлвуд окончательно вернулся в Кембридж, он попросил Петроса поработать вместе с ним и с Харди над статьей, которую они начинали с Рамануджаном. (Бедняга к этому времени был серьезно болен и почти все время проводил в санатории.) В это время оба великих специалиста по теории чисел обратили свои усилия на гипотезу Римана – эпицентр большинства недоказанных главных теорем в аналитическом подходе. Доказательство интуитивной гипотезы Бернхарда Римана о нулях его дзета-функции вызвало бы положительный эффект домино и породило бы доказательства бессчетных фундаментальных теорем теории чисел. Петрос предложение принял (покажите мне честолюбивого молодого математика, который бы отказался!), и они втроем совместно опубликовали две работы в 1918 и 1919 годах – те самые, которые нашел в библиографическом указателе мой друг Сэмми Эпштейн.

Ирония судьбы в том, что это были его последние опубликованные работы.

После первой статьи Харди, непогрешимый судья математического таланта, предложил Петросу принять должность в Тринити-колледже и остаться в Кембридже, войдя на постоянной основе в их элитную команду.

Петрос попросил время подумать. Конечно, предложение было невероятно лестным, и перспектива продолжить сотрудничество казалась на первый взгляд исключительно заманчивой. Постоянная работа в контакте с Харди и Литлвудом породит, без сомнения, великолепные работы, которые обеспечат его резкий взлет среди научной общественности. К тому же оба эти человека Петросу нравились. Общение с ними не только было приятно, но и чертовски стимулировало работу. Сам воздух, которым они дышали, был насыщен яркой и богатой математической мыслью.

Да, но несмотря на все это, перспектива остаться наполняла его тревогой.

Оставшись в Кембридже, он поплывет предсказуемым курсом. Он будет делать хорошие, даже исключительные работы, но его развитие будет определяться Харди и Литлвудом. Их проблемы будут его проблемами, и – хуже всего – их слава всегда будет затмевать его славу. Если они в конце концов докажут гипотезу Римана (Петрос надеялся, что так и будет), это станет событием величайшей важности, результатом, который потрясет мир. Но разве это будет его результат? На самом деле – разве даже третья часть почестей, причитающаяся на его долю, достанется ему целиком? Разве не выйдет скорее так, что его слава затмится славой двух его блестящих коллег?

Всякий, кто говорит, что учеными – даже адептами чистейшей науки, самыми абстрактными, парящими в горних высях математиками – движет исключительно Стремление К Истине Ради Блага Человечества, либо понятия не имеет, о чем говорит, либо нагло лжет. Да, наиболее возвышенно настроенные ученые вполне могут быть безразличны к материальной выгоде, но нет ни одного, которым не движет главным образом честолюбие и сильнейший дух соревнования. (Разумеется, в случае великих математических достижений число соперников ограничено, и чем более масштабно это достижение, тем сильнее ограничена группа. За приз сражается избранное меньшинство, лучшие из лучших, соревнование становится истинной гигантомахией – борьбой гигантов). Математик, пускаясь в серьезное исследование, может намереваться преследовать Истину, но мечтать он будет о Славе.

Мой дядя не был исключением – это он признал в разговоре со мной совершенно искренне. После Берлина и разочарования в «милой Изольде» он жаждал в математике великого, почти невероятного успеха, полного триумфа, который принесет ему мировую славу и (как он надеялся) повергнет жестокосердную деву перед ним на колени. И этот триумф, чтобы быть полным, должен принадлежать ему и только ему, а не быть поделенным между двоими или троими.

И еще против того, чтобы остаться в Кембридже, говорило время. Понимаете, математика – это игра людей молодых. Она одно из немногих занятий человека (и в этом она похожа на спорт), где молодость – неотъемлемое условие высших достижений. Петрос, как и всякий молодой математик, знал гнетущую статистику: практически никогда в истории его науки великое открытие не было сделано человеком тридцати пяти или сорока лет. Риман умер в тридцать девять, Нильс Хенрик Абель – в двадцать семь, а Эварист Галуа трагически погиб в двадцать, но их имена вписаны в историю математики золотом по мрамору. «Дзета-функция Римана», «Абелевы интегралы» и «Группы Галуа» – бессмертное наследие для математиков грядущих поколений. Пусть Эйлер и Гаусс работали и доказывали теоремы в пожилом возрасте, но их фундаментальные открытия были сделаны в ранней молодости. В любой другой области двадцатичетырехлетний Петрос был бы многообещающим новичком, и его ждали бы годы и годы богатой творческой жизни. А в математике он уже был на пике своего развития.

Он прикинул, что у него в лучшем случае есть еще лет десять, когда он может ошеломить человечество (а также «милую Изольду») великим, невероятным, колоссальным достижением. А потом его сила рано или поздно начнет увядать. Техника и знание, даст Бог, выживут, но искра, которая поджигает этот волшебный фейерверк, блестящая изобретательность и живой дух атаки, необходимые для истинно Великого Открытия (мечта о решении проблемы Гольдбаха все сильнее занимала его мысли), ослабеют, если не исчезнут совсем.

И после не слишком долгих размышлений Петрос решил, что Харди и Литлвуду придется дальше идти без него.

С этой минуты он не может позволить себе потерять ни одного дня. Впереди лежат самые плодотворные годы, неодолимо зовущие его. Он должен немедленно начать работу над проблемой.

А насчет того, что за проблема, все ясно. Это может быть только один из великих открытых вопросов, которые в случайном разговоре несколько лет назад упомянул Каратеодори, – ничто меньшее не устроило бы честолюбие Петроса. Из этих вопросов гипотеза Римана уже находилась в руках Харди и Литлвуда, и простая научная этика, не говоря уже об осторожности, требовала оставить ее в покое. Что касается последней теоремы Ферма, то методы, которые традиционно использовались для попыток ее доказательства, были, на вкус Петроса, слишком алгебраическими. Итак, выбор оказывался очень прост: машина, которая повезет его к исполнению мечты о славе и бессмертии, не может быть ничем иным, кроме как проблемой Гольдбаха с ее скромно звучащей формулировкой.

Предложение занять кафедру анализа в Мюнхенском университете пришло чуть раньше и оказалось очень вовремя. Эта должность была бы идеальной. Ранг профессора – косвенная награда за полезность метода Папахристоса для армии кайзера – даст Петросу свободу от излишней преподавательской нагрузки и обеспечит финансовую независимость от отца, чтобы у того не было искушения вернуть сына в Грецию и заставить заниматься семейным предприятием. В Мюнхене он будет избавлен от посторонних обязанностей. Несколько лекционных часов – не слишком большая потеря времени, напротив, живая связь с техникой анализа, которую он будет применять в своей работе.

Меньше всего Петросу хотелось, чтобы другие лезли в его задачу. Оставляя Кембридж, он намеренно скрыл свои следы дымовой завесой. Он не только не сказал Харди и Литлвуду, что отныне будет работать над проблемой Гольдбаха, но создал у них впечатление, что будет продолжать заниматься их любимой гипотезой Римана. И в этом отношении Мюнхен тоже был идеален: его математический факультет не был особенно прославленным, как Берлинский или почти легендарный Геттингенский, и потому Петрос будет изолирован от главных центров математических сплетен и назойливого любопытства.

Летом 1919 года Петрос въехал в темную квартиру на втором этаже (он считал, что излишек света несовместим с абсолютной сосредоточенностью) неподалеку он университета. Он познакомился с новыми коллегами и обговорил программу преподавания со своими ассистентами, которые почти все были старше его. Потом он организовал у себя дома рабочую обстановку, в которой отвлекающие моменты были сведены к минимуму. Его домоправительнице, еврейской даме средних лет, овдовевшей в последнюю войну, было абсолютно недвусмысленно сказано, что когда Петрос находится в кабинете, тревожить его нельзя ни под каким видом.

Прошло уже больше сорока лет, но мой дядя с исключительной ясностью помнит тот первый день, когда он начал работу.

Солнце еще не взошло, когда он уже сел за стол, взял толстую авторучку и написал на чистом белом листе бумаги:

УТВЕРЖДЕНИЕ. Любое четное число, большее 2, может быть представлено в виде суммы двух простых.

ДОКАЗАТЕЛЬСТВО. Допустим, что данное утверждение ложно. Тогда существует целое число n, такое, что 2n не может быть выражено в виде суммы двух простых чисел, т. е. для любого простого числа p ‹ 2n число 2n – p является составным…

После нескольких месяцев напряженной работы он начал оценивать истинные размеры проблемы и отметил наиболее очевидные тупики. Он уже мог очертить общую стратегию своего подхода и сформулировать некоторые промежуточные результаты, которые необходимо было доказать. Следуя военной терминологии, он называл их «господствующими высотами, которые надо занять перед решительной атакой на саму Проблему».

Разумеется, весь подход был основан на аналитическом методе.

Теория чисел как в аналитическом, так и в алгебраическом вариантах имеет один и тот же предмет изучения, а именно – свойства натуральных чисел 1, 2, 3, 4, 5, а также их взаимоотношения. Как физические исследования часто сводятся к изучению элементарных частиц материи, так и многие главные проблемы высшей арифметики сводятся к вопросам простых чисел (натуральных чисел, не имеющих других делителей, кроме 1 и себя самих, например, 2, 3, 5, 7, 11…) – неделимых квантов числовой системы.

Древние греки, а вслед за ними и великие математики эпохи европейского Просвещения, такие как Пьер де Ферма, Леонард Эйлер и Карл Фридрих Гаусс, нашли целые залежи интереснейших теорем о простых числах (мы уже упоминали доказательство Евклида бесконечности множества простых чисел). И все же к середине девятнадцатого столетия самые фундаментальные свойства простых чисел оставались вне досягаемости математиков.

Главными среди этих вопросов были следующие два: «распределение» простых чисел (т.е. количество простых чисел, меньших заданного натурального n) и картина их следования, неуловимая формула, по которой, зная простое число p_n, можно найти следующее простое – p_n+1. Часто (быть может, бесконечно часто, согласно одной гипотезе) простые числа различаются только на 2, идут парами, например, 5 и 7, 11 и 13, 41 и 43 или 9857 и 9859 [13]. В других же случаях два последовательных простых числа могут быть разделены сотнями, тысячами, миллионами составных чисел – вообще-то очень просто доказать, что для любого наперед заданного натурального числа k можно найти идущие подряд k натуральных чисел, среди которых нет ни одного простого [14].

Отсутствие видимого порядка в организации последовательности простых чисел мучило математиков много веков подряд и во многом придавало теории чисел такой захватывающий интерес. Да, это была великая загадка, достойная самых возвышенных умов: раз простые числа – строительные блоки для натуральных чисел, а натуральные числа – основа логического понимания космоса, как может быть, что их вид не определяется законом? Почему в этом случае не очевидна «божественная геометрия»?

Аналитическая теория чисел родилась в 1837 году вместе с поразительным доказательством Дирихле бесконечности множества простых чисел в арифметических прогрессиях. Но пика своего развития она достигла только к концу века. За несколько лет до Дирихле Карл Фридрих Гаусс высказал догадку об «асимптотической» формуле для числа простых чисел, меньших заданного целого n (асимптотическая – это значит дающая все более точный результат по мере роста n). Но ни он, ни кто-либо другой не смог дать даже намек на доказательство. Потом в 1859 году Бернхард Риман ввел бесконечный ряд комплексных чисел [15], с тех пор известный под названием «дзета-функции Римана», который обещал стать крайне полезным инструментом. Однако для эффективного применения этого инструмента специалистам по теории чисел пришлось оставить традиционные, алгебраические (так называемые элементарные) методы и прибегнуть к методам комплексного анализа, то есть к исчислению бесконечно малых на комплексной плоскости.

Прошло несколько десятилетий, и Адамар и Балле-Пуссен смогли доказать асимптотическую формулу Гаусса с помощью дзета-функции Римана (с тех пор этот результат известен как «Закон распределения простых чисел»). Аналитический подход вдруг сделался волшебным ключом к самым глубоким тайнам теории чисел.

Когда Петрос начал работу над проблемой Гольдбаха, аналитический подход был на пике возлагаемых на него надежд.

Потратив несколько первых месяцев на ознакомление с масштабами проблемы, Петрос решил, что будет действовать с помощью теории разложений (различных способов представления целого числа в виде суммы) – еще одного приложения аналитического метода. Помимо центральной для этого круга вопросов теоремы, доказанной Харди и Рамануджаном, существовала также гипотеза Рамануджана (одно из его знаменитых «предчувствий»), которую Петрос надеялся использовать как решающую ступень на подходе к проблеме Гольдбаха – если только ему удастся эту гипотезу доказать.

Он написал Литлвуду, спросив его как можно более осторожно, были ли какие-либо работы в этой области за последнее время, и постарался, чтобы вопрос выглядел простым «интересом коллеги». Литлвуд ответил отрицательно, прислав при ответе новую книгу Харди «Некоторые знаменитые проблемы теории чисел». В ней содержалось своего рода доказательство утверждения, которое называется «второй», или «другой», проблемой Гольдбаха [16]. Это так называемое доказательство имело фундаментальную лакуну: оно опиралось на гипотезу Римана – не доказанную. Петрос прочел его и покровительственно улыбнулся. Да, Харди дошел до отчаяния, если публикует результаты, основанные на недоказанных предположениях! Основная же проблема Гольдбаха, Проблема с большой буквы, не удостоилась даже упоминания. Петросу ничего не грозило.

Он вел свою работу в полной тайне, и чем глубже исследования уводили его в глубь terra incognita [17], определенной Проблемой, тем ревностнее он заметал следы. Самым любопытным коллегам он давал тот же уводящий в сторону ответ, который дал Харди и Литлвуду: он развивает работу, которую начал с ними в Кембридже, продолжает совместную работу над гипотезой Римана. Со временем он стал осторожен до параноидальности. Чтобы коллеги не сделали правильного вывода по списку читаемой им литературы, он начал искать способы маскировать свои заказы. Чтобы спрятать книгу, которая была ему нужна, он указывал в требовании еще три-четыре, не имеющие отношения к делу, или заказывал журнальную статью, только чтобы получить в руки том, содержащий другую статью, которая ему была действительно нужна, и изучал его вдали от посторонних глаз в полном уединении своего кабинета.

Весной того же года Петрос получил еще одно короткое письмо от Харди, где говорилось о смерти Сринивасы Рамануджана от туберкулеза в трущобах Мадраса. Непосредственная реакция на эту новость Петроса озадачила и даже огорчила. Под поверхностным слоем скорби об утрате выдающегося математика и приятного, хорошего и скромного друга в глубине души Петрос ощутил дикую радость от того, что этот феноменальный мозг уже не занимается теорией чисел.

Понимаете, никого другого он не боялся. Его два самых квалифицированных соперника, Харди и Литлвуд, слишком были заняты гипотезой Римана, чтобы серьезно думать о проблеме Гольдбаха. А Давид Гильберт, единодушно признанный величайшим из живущих математиков, или Жак Адамар, единственный, кроме названных, специалист по теории чисел, с которым стоило считаться, оба уже были не более чем уважаемыми ветеранами – почти шестьдесят лет, что для творческого математика равносильно глубокой старости. Но Рамануджана он боялся. Этот уникальный интеллект Петрос считал единственной силой, способной похитить его приз. Несмотря на сомнения в верности гипотезы, которыми он поделился с Петросом, стоило Рамануджану сосредоточить на этой проблеме свой гений… Кто знает, быть может, он доказал бы гипотезу даже вопреки самому себе; быть может, его возлюбленная богиня Намакири предложила бы ему во сне решение, аккуратно записанное санскритом на свитке пергамента!

Теперь, когда он умер, исчезла реальная опасность, что кто-то придет к решению раньше Петроса.

И все же, когда великая математическая школа в Геттингене пригласила Петроса прочесть мемориальную лекцию о вкладе Рамануджана в теорию чисел, он тщательно избегал любых упоминаний своих работ по разложениям, чтобы никто не вздумал проследить их возможные связи с проблемой Гольдбаха.

К концу лета 1922 года (по совпадению, в тот самый день на его страну обрушились новости о разрушении Смирны) Петрос неожиданно встал перед лицом своей первой большой дилеммы.

Случай был вообще-то счастливый: во время долгой прогулки по берегу Шпайхерзее его внезапно посетило озарение, которому предшествовали долгие месяцы изматывающей работы. Он тут же сел за столик в небольшой пивной и записал открытие в блокноте, который всегда носил с собой. Потом на первом же поезде он отправился в Мюнхен и просидел за столом от сумерек до рассвета, прорабатывая детали и просматривая свои рассуждения снова и снова. Закончив работу, он второй раз в своей жизни (первый был связан с Изольдой) ощутил чувство окончательного достижения, абсолютного счастья. Он сумел доказать гипотезу Рамануджана!

В первые годы своей работы над Проблемой он накопил довольно много интересных промежуточных результатов, так называемых лемм, или малых теорем, среди которых был безусловный и богатый материал, достойный публикации. Но у него никогда даже не было искушения их обнародовать. Хотя результаты были вполне приличные, ни один из них не мог бы считаться серьезным открытием – даже по эзотерическим стандартам специалистов по теории чисел.

Да, но сейчас было по-другому.

Проблема, решенная им сегодня днем на прогулке, имела особую важность. По отношению к работе над Проблемой она, конечно, была всего лишь промежуточным шагом, а не конечной целью. И все же это была глубокая и оригинальная теорема, доказанная им самим, такая, которая открывала новые горизонты теории чисел. Она проливала новый свет на вопросы разложений, используя прежнюю теорему Харди-Рамануджана таким способом, о котором никто раньше и не подозревал, не говоря уже о том, чтобы применять. Публикация, несомненно, принесет ему признание в математическом мире, признание куда большее, чем дал его метод решений дифференциальных уравнений. Она вознесет его в первые ряды небольшой, но избранной международной общины специалистов по теории чисел практически на тот же уровень, где обретаются звезды первой величины – Адамар, Харди и Литлвуд.

Опубликовав свое открытие, он также откроет дорогу к Проблеме другим математикам, которые построят на его теореме новые результаты и раздвинут границы науки так, как исследователь-одиночка, как бы он ни был силен, не может даже надеяться. Эти результаты, в свою очередь, помогут ему в дальнейших поисках решения проблемы Гольдбаха. Иными словами, опубликовав «Теорему Папахристоса о разложении» (разумеется, надо будет скромно подождать, пока коллеги дадут ей это название), он приобретет легион помощников. К сожалению, у этой медали есть и другая сторона: один из новых бесплатных (и непрошеных) помощников может случайно наткнуться на лучший способ применить его теорему и, не дай Бог, первым решить проблему Гольдбаха.

Петрос раздумывал недолго – опасности сильно перевешивали выгоды. Публикации не будет. «Теорема Папахристоса о разложении» останется его личной, тщательно охраняемой тайной.

Рассказывая мне об этом, дядя Петрос назвал это решение поворотным пунктом своей жизни. С того момента, сказал он, трудности стали громоздиться на трудности.

Воздержавшись от публикаций своего первого по-настоящему важного вклада в математику, он подставил себя под удвоенный пресс времени. Помимо постоянно гнетущего чувства, что вот идут дни, недели, месяцы и годы, а он все еще далек от желанной цели, теперь возникло и беспокойство, что кто-то повторит его открытие независимо и украдет его славу.

Официальные успехи, достигнутые им прежде (метод, названный его именем, и кафедра в университете), вполне можно было считать выдающимися. Но у математиков свой отсчет времени. Сейчас Петрос был на абсолютном пике своих возможностей, в расцвете сил, который долго продлиться не мог. Настало время совершить великое открытие – если оно вообще ему предстояло.

При его замкнутом образе жизни не было никого, кто мог бы облегчить ему это бремя.

Одиночество ученого, занимающегося математикой, не похоже на другие виды одиночества. Он в самом буквальном смысле слова живет в абсолютно недостижимой вселенной – как для общества, так и для своего ближайшего окружения. Даже самые близкие к нему люди не могут по-настоящему радоваться его радостью или разделять его горести, потому что не могут понять их содержания.

Единственное общество, к которому принадлежит работающий математик, – это его коллеги, но от них Петрос отделил себя сознательно. В течение своего первого года в Мюнхене он иногда подвергался традиционному академическому гостеприимству по отношению к новичкам. Но если он принимал приглашение, то притворяться нормальным, вести себя приятно и поддерживать светскую болтовню было просто пыткой. Приходилось все время удерживаться, чтобы не задуматься над вопросами теории чисел, и подавлять частые импульсы быстро бежать домой и сесть за стол, записать пришедшие мысли. К счастью, то ли из-за его обычных отказов, то ли оттого, что все видели, как ему это неловко, его стали приглашать все меньше и меньше и, наконец, к его великому облегчению, перестали приглашать совсем.

Нет нужды добавлять, что он так и не женился. Рациональное объяснение, которое он мне привел, состояло в том, что жениться на другой женщине означало бы изменить его великой любви, «милой Изольде», и это объяснение, конечно, было только предлогом. На самом деле он просто отлично понимал, что его образ жизни не допускает присутствия другого лица. Одержимость работой не отпускала Петроса ни на миг. Проблема Гольдбаха требовала его целиком: телом, душой и временем.

Летом 1925 года дядя Петрос получил второй важный результат, который в комбинации с «Теоремой о разложении» открывал новые подходы ко многим классическим проблемам простых чисел. Согласно его собственному чрезвычайно справедливому и весьма компетентному мнению, его работа составляла истинный прорыв. Искушение опубликовать результаты стало мучительным. Оно терзало его неделями – но он снова сумел устоять. Он вновь решил сохранить свои результаты для себя, а не открывать их для нежелательных помощников. Никакие промежуточные результаты, как бы важны они ни были, не отвлекут его от конечной цели. Он решит проблему Гольдбаха или будь он проклят!

В ноябре того же года ему исполнилось тридцать – символический возраст для математика-исследователя, фактически первая ступень к зрелому возрасту.

Дамоклов меч, висящий где-то в темноте над головой (на нем было написано «Увядание творческих сил»), стал теперь почти видимым. Все сильнее и сильнее ощущал его Петрос, сгорбившись за своим столом. Незримые песочные часы, отмерявшие время творческого расцвета, постоянно маячили на заднем плане сознания, вызывая напряжение и страх. В каждый момент бодрствования его грызла тревога, что он уже, быть может, спускается с вершины своих интеллектуальных возможностей. Назойливыми мухами жужжали в мозгу вопросы: а будут ли у него еще прорывы такого масштаба, как первые два результата? Не начался ли уже неизбежный спад, которого он пока не замечает? Любое мелкое проявление забывчивости, любая ошибочка в вычислениях, каждое нарушение сосредоточенности вызывало все тот же зловещий рефрен: «Не миновал ли я свой расцвет?»

Краткий визит родственников, которых он много лет не видел (тот, который описал мне отец), был им сочтен грубым и наглым вторжением. То недолгое время, что он провел с родителями и младшими братьями, он ощущал как украденное у его работы, и каждый миг, проведенный ради них не за письменным столом, казался ему малой дозой математического самоубийства. К концу их пребывания он просто выходил из себя.

Не терять времени – это стало настоящей одержимостью до такой степени, что он изгнал из своей жизни все, не относящееся к проблеме Гольдбаха, – все, кроме двух вещей, которые он сократил до минимума: преподавание и сон. И все же сна было меньше, чем необходимо. Постоянная тревога принесла с собой бессонницу, усиливавшуюся от потребления увеличенных доз кофе – горючего, на котором работают математики. С течением времени постоянные мысли о проблеме Гольдбаха лишили его возможности отдыхать. Заснуть или не просыпаться становилось все труднее, и часто приходилось прибегать к снотворным таблеткам. Сначала – разово, потом – постоянно, увеличивая дозы до угрожающих, почти до зависимости, и при этом без желательного эффекта.

Примерно в это время его дух получил совершенно неожиданную поддержку в виде довольно экзотического сна. Несмотря на полное неверие в сверхъестественное, Петрос счел этот сон пророческим, очевидным знамением непосредственно с Математических Небес.

Такое бывает с учеными, полностью погруженными в трудную задачу: поглощенность мыслями не оставляет даже во сне, и хотя Петрос никогда не был почтен ночными визитами рамануджановой богини Намакири или другого уважаемого божества (факт, который не должен нас удивлять, учитывая его закоренелый агностицизм), но после первого года занятий проблемой Гольдбаха ему стали сниться математические сны. Прежние сны любовного блаженства в объятиях «милой Изольды» сделались реже и уступили место снам о Четных Числах, которые являлись в виде двойняшек. Они устраивали сложные неземные пантомимы, служа фоном к Простым Числам – гермафродитам, двуполым человеческим существам. В отличие от безмолвных Четных Простые часто болтали между собой, обычно на непонятном языке, и одновременно отплясывали чечетку. (Петрос допускал, что хореография была навеяна балетом Стравинского «Весна священная», который он видел в начале своего пребывания в Мюнхене, когда у него еще было время на подобные пустяки.) Изредка какое-нибудь из этих созданий говорило, и тогда на классическом греческом – может быть, в знак уважения к Евклиду, который наградил их бесконечностью. Даже когда эти сбивчивые речи и имели лингвистический смысл, математическое их содержание было либо тривиально, либо бессмысленно. Петрос нарочно запомнил одно такое высказывание: «хапантес протон перритои», что означает: «все простые числа четны» – утверждение очевидно ложное. (Но если взять другой смысл слова «перритои», это может означать «все простые числа бесполезны», интерпретация, которая – любопытно отметить – полностью ускользнула от внимания дяди.)

Но иногда, в редких случаях, в этих снах бывало что-то существенное. В речах сценических персонажей попадались намеки, которые направляли мысль Петроса по интересным и неисследованным путям [18].

Сон, который так поднял его дух, пришел через несколько дней после того, как Петрос доказал свой второй важный результат. Сон был не чисто математический, а скорее панегирический, состоящий из одного образа, блестящей живой картины, но такой неземной красоты! С одной стороны стоял Леонард Эйлер, с другой – Христиан Гольдбах (никогда не видя его портретов, дядя все же сразу понял, что это он). Оба держали золотой венец над центральной фигурой, и это был не кто иной, как он, Петрос Папахристос. Всю триаду озарял нимб ослепительного света.

Смысл сна был совершенно ясен: именно ему предстоит решить проблему Гольдбаха.

Настроение дяди снова метнулось к оптимизму, и он с новым усердием накинулся на работу. Теперь он должен вложить в нее все свои силы. Никаких отвлечений он себе позволить не может.

Недавно появившиеся боли в желудке (по странному совпадению, чаще всего они случались тогда, когда мешали исполнению его университетских обязанностей) – результат постоянного напряжения, в котором он себя держал, – дали ему необходимый предлог. Вооруженный заключением специалиста, дядя пошел к декану математического факультета и попросил двухгодичный неоплачиваемый отпуск.

Декан, слабый математик, но ревностный бюрократ, явно ждал случая поставить профессора Папахристоса на место.

– Я прочел рекомендации вашего врача, герр профессор, – сказал он довольно неприветливо. – Вы явно страдаете – как и многие на нашем факультете – гастритом, что не является угрожающим состоянием. Вы не считаете, что два года – это слишком?

– Видите ли, герр декан, – промямлил Петрос, – у меня еще наступил самый важный момент в моей работе. Во время двухгодичного отпуска я ее закончу.

Декан выказал неподдельное удивление.

– Работе? О, я даже понятия не имел! Понимаете, тот факт, что вы ничего не публиковали за все эти годы, привел ваших коллег к заключению, что вы как ученый бездеятельны. – Петрос знал, что следующий вопрос неизбежен. – Кстати, над чем именно вы работаете, герр профессор?

– Н-ну, – неуверенно протянул Петрос, – размышляю над некоторыми вопросами теории чисел.

Декан, человек до мозга костей практический, считал теорию чисел – область, знаменитую тем, что ее результаты не имеют приложений в физических науках, – чистейшей тратой времени. Его собственные интересы относились к области дифференциальных уравнений, и тогда, вначале, он рассчитывал, что, приглашая на факультет автора метода Папахристоса, поставит свое имя на какой-нибудь совместной публикации. Как вы понимаете, этого так и не случилось.

– Вы имеете в виду теорию чисел вообще, герр профессор?

Какое-то время Петрос пытался всячески увиливать, чтобы не выдать истинный предмет своих занятий, но когда понял, что ему никак не убедить декана в серьезности своей работы, открыл правду.

– Я работаю над проблемой Гольдбаха, герр декан. Но ради Бога, не говорите никому!

Декан был поражен.

– Да? И каковы ваши успехи?

– Довольно значительны.

– То есть у вас есть очень интересные промежуточные результаты? Я правильно вас понял?

Петрос почувствовал, что идет по канату, натянутому над пропастью. Что он может рассказать, не рискуя?

– Ну, я… – Он заерзал в кресле, обливаясь потом. – На самом деле, герр декан, я думаю, что нахожусь в одном шаге от окончательного решения. Если вы мне дадите мои два года неоплачиваемого отпуска, я постараюсь его закончить.

Декан знал проблему Гольдбаха – кто же ее не знает? Несмотря на то что она относилась к заумным высям теории чисел, проблема была знаменитой. Успех профессора Папахристоса (который, несмотря ни на что, пользовался репутацией выдающегося ума) будет очень на пользу университету, математическому факультету и, разумеется, ему, декану этого факультета. Прикинув это все, декан широко улыбнулся Петросу и сообщил, что ничего против его просьбы не имеет.

Когда Петрос зашел потом поблагодарить и попрощаться, декан весь таял в улыбках.

– Удачи вам с Проблемой, герр профессор! Жду вас обратно с великим результатом!

Получив свои два благодатных года, дядя переехал в Инсбрук в Австрийском Тироле и снял небольшой коттедж. Для пересылки писем он указал только местное почтовое отделение до востребования. На новом месте его абсолютно никто не знал, и не надо было бояться даже тех небольших отвлечений, которые мешали в Мюнхене: встреча на улице с дальним знакомым, назойливая забота домоправительницы (ее он оставил приглядывать за пустым домом). Одиночество было абсолютным и ненарушаемым.

В Инсбруке в жизни Петроса произошло изменение, благотворно сказавшееся на его настроении и, в силу этого, на его работе: он открыл для себя шахматы.

Однажды вечером во время привычной прогулки он зашел в кафе, которое оказалось местом собраний шахматного клуба. В детстве Петросу показали ходы фигур, и несколько партий он в жизни сыграл, но до этого вечера не понимал, насколько глубока эта игра. Когда он задумчиво попивал какао, его внимание привлекла разворачивающаяся за соседним столиком партия, и он стал смотреть с возрастающим интересом. На следующий вечер ноги сами привели его туда же, и через день случилось то же самое. Поначалу только наблюдая, он постепенно стал постигать захватывающую логику игры.

Через несколько дней он принял приглашение сыграть и проиграл, что вызвало у него раздражение, особенно когда он узнал, что его партнер по роду занятий – погонщик скота. В эту ночь дядя Петрос лег спать поздно, весь вечер прокручивая в мозгу ходы и пытаясь определить ошибки. В последующие вечера он проиграл еще несколько партий, но потом одну выиграл и ощутил огромную радость – чувство, которое подстегнуло его одержать еще несколько побед.

Постепенно он сделался завсегдатаем кафе и вступил в местный шахматный клуб. Один из членов клуба сообщил ему об огромном объеме накопленной мудрости, касающейся первых ходов партии, – эта мудрость называлась «теория дебютов». Петрос взял в библиотеке учебник и купил себе шахматы, которые оставались с ним и в старости у него дома в Экали. Он всегда поздно засиживался по вечерам, но в Инсбруке – не из-за Гольдбаха. С расставленными на доске фигурами, с книгой в руке, он проводил часы за изучением основных начал – «Испанской партии», «Королевского и ферзевого гамбитов», «Сицилианской защиты».

Вооруженный некоторой теорией, он стал выигрывать все чаще и чаще, к своему огромному удовлетворению. Разумеется, проявляя рвение неофита, он несколько перебирал, проводя за шахматами часы, принадлежащие математике, приходя в кофейню все раньше и раньше и даже обращаясь к шахматной доске в дневные часы, чтобы проанализировать вчерашние партии. Однако вскоре взял себя в руки и ограничил занятия шахматами вечерними прогулками и часом занятий перед сном (изучение дебюта или разбор знаменитой партии). Несмотря на это, уезжая из Инсбрука, дядя уже был непререкаемым местным чемпионом.

Шахматы серьезно изменили его жизнь. С тех пор, как он посвятил себя решению проблемы Гольдбаха – а это было почти десять лет назад, – Петрос почти никогда не отдыхал от своей работы. Но для математика важно иногда отвлекаться от проблемы, которой он занят. Чтобы переварить сделанную работу и проанализировать ее результаты на уровне подсознания, периоды покоя так же необходимы, как периоды работы на износ. Насколько исследование математических концепций оживляет спокойный ум, настолько же оно может быть невыносимо для ума усталого, истощенного постоянными усилиями.

Из его знакомых математиков каждый отдыхал по-своему. Для Каратеодори отдыхом были его административные обязанности в Берлинском университете. У коллег по математическому факультету бывало по-разному: для семейных отдыхом обычно была семья, для некоторых – спорт, для других коллекционирование или посещение театров, концертов и других развлечений, которых в Мюнхене достаточно. Но Петросу ничего из этого не подходило – ничто его не занимало настолько, чтобы отвлечь от работы. В какой-то момент он пытался читать детективы, но когда исчерпал расследования ультрарационалиста Шерлока Холмса, ничто другое уже не могло удержать его внимания. Долгие вечерние прогулки никак нельзя было счесть отдыхом. Тело его гуляло по городу или на природе, вдоль безмятежного озера или по оживленной улице, а ум был постоянно занят Проблемой, и сама ходьба служила лишь способом сосредоточиться на работе.

Шахматы, казалось, были ниспосланы ему самим небом. Будучи по своей природе игрой для ума, они требовали сосредоточенности. Невнимание всегда наказывается, разве что в игре с намного более слабым противником, да и тогда бывает, что за него приходится платить. Петрос погрузился в изучение партий великих шахматистов (Стейница, Алехина, Капабланки) с сосредоточенностью, знакомой ему ранее только по работе математика. Добиваясь победы над лучшими игроками Инсбрука, он обнаружил, что можно – пусть ненадолго – полностью отвлечься от проблемы Гольдбаха. Встречаясь с сильным партнером, он, к своему крайнему удивлению, замечал, что несколько часов вообще не может думать ни о чем, кроме шахмат. Эффект оказался живительным. Наутро после игры Петрос брался за Проблему с ясным и освеженным умом; открывались пути и связи, которых он раньше не видел, и это как раз тогда, когда он начал бояться, что иссякает.

Расслабляющий эффект шахмат позволил дяде отучить себя от снотворного. Отныне, если ночью его одолевали бесплодные навязчивые мысли о Проблеме, если усталый разум вертелся и блуждал в бесконечном математическом лабиринте, дядя вставал, садился за шахматную доску и разбирал какую-нибудь интересную партию. Погружаясь в нее, он временно забывал математику, веки тяжелели, и он до утра засыпал в кресле, как младенец.

Перед концом двухлетнего отпуска Петрос принял судьбоносное решение: он опубликует свои два открытия – «Теорему Папахристоса о разложении» и вторую теорему.

Но это, следует подчеркнуть, отнюдь не потому, что дядя решил удовольствоваться малым. Никаких пораженческих настроений по поводу решения проблемы Гольдбаха у него не было. Работая в Инсбруке, Петрос спокойно изучил все работы в этой области. Он проработал результаты, полученные до него другими, и проанализировал ход собственных исследований. Рассмотрев в ретроспективе свои результаты, он убедился в следующем: а) две его теоремы о разложениях были сами по себе важными результатами и б) они не приблизили его к решению проблемы – первоначальный план пока не дал результатов.

Душевный мир, которого он достиг в Инсбруке, принес Петросу фундаментальное озарение: дефект его подхода состоял в том, что он принял на вооружение аналитический метод. Он понял, что его увлек в сторону успех Адамара и Валле-Пуссена, доказавших теорему о распределении простых чисел, а также – и в особенности – авторитет Харди. Иными словами, ему затуманили зрение требования математической моды (да-да, такая вещь существует!), требования, не в большей степени имеющие право считаться Математической Истиной, чем ежегодные капризы гуру от кутюр – Платоновым Идеалом Красоты. Теоремы, обоснованные строгими доказательствами, являются, конечно, абсолютными и вечными, но методы, которыми их доказывают, – определенно нет. Выбор методов по определению конъюнктурен – вот почему они так часто меняются.

Мощная интуиция Петроса говорила ему теперь, что аналитический метод себя исчерпал. Настало время для чего-то нового, или, точнее говоря, чего-то старого, возвращения к древнему и проверенному временем подходу к тайнам чисел. На его плечи, решил он, легло тяжкое бремя заново определить направление развития теории чисел на будущее: решение проблемы Гольдбаха, полученное элементарной, алгебраической техникой, решит вопрос раз и навсегда.

А что касается его первых результатов – теоремы о разложении и второго результата, – их можно теперь без риска отдать математической общественности. Поскольку они получены аналитическим методом (который более не казался полезным для решения Проблемы), их публикация не грозит тем, что кто-то опередит его в получении главного результата.

Когда Петрос вернулся в Мюнхен, домоправительница обрадовалась, увидев герра профессора в столь цветущем виде. Она его даже с трудом узнала; как она сказала, «он просто помолодел, просто сиял здоровьем».

Была середина лета, и Петрос, не обремененный академическими нагрузками, начал составлять монографию о своих двух теоремах с доказательствами. Пожиная плоды десятилетних усердных трудов на ниве аналитического метода, видя их в конкретной форме, с началом, серединой и концом, полностью и четко представленными и изложенными, Петрос был вполне доволен. Он понимал, что, хотя и не решил пока Проблему, сделал в математике выдающуюся работу. Не приходилось сомневаться, что публикация двух его теорем принесет ему первые серьезные научные лавры. (Выше уже было сказано, что он сбрасывал со счетов прикладной результат «метода Папахристоса решения дифференциальных уравнений».) Он мог теперь даже позволить себе помечтать о том, что его ждет. Он уже видел восторженные письма коллег, поздравления на факультете, приглашения прочитать лекции о своих результатах в главных университетах мира. Он даже видел получение международных наград и премий. А почему бы и нет? Его теоремы этого заслуживают.

С началом учебного года (продолжая работать над монографией) Петрос возобновил преподавательскую деятельность и был удивлен, что чтение лекций приносит ему удовольствие. Усилия, требуемые для изложения и объяснения материала в понятном студентам виде, увеличивали радость от понимания того, что он излагает. Декан факультета тоже был доволен – не только повышением качества лекций, о котором сообщали и ассистенты, и студенты, но главным образом информацией о том, что профессор Папахристос готовит к печати монографию. Два года в Инсбруке помогли. Пусть даже готовящаяся работа не содержит решения проблемы Гольдбаха, уже поговаривали, что там есть крайне важные результаты.

Монография была закончена сразу после Рождества, и в ней оказалось около двухсот страниц.

Она была озаглавлена с чуть лицемерной скромностью, с которой многие математики публикуют важные результаты: «Некоторые замечания о проблеме разложений». Петрос отдал ее перепечатать и направил экземпляр Харди и Литлвуду, прося их просмотреть работу и сообщить, не упустил ли он какой-либо логической ловушки и не допустил ли скрытой ошибки. На самом деле он отлично знал, что ни ловушек, ни ошибок там нет: он просто тешил себя мыслью об изумлении и восхищении, которое охватит этих двух столпов теории чисел. Фактически он уже грелся в лучах их похвал.

Отослав рукопись, Петрос решил, что может позволить себе каникулы перед тем, как снова полностью отдаться Проблеме. Следующие несколько дней были всецело посвящены шахматам.

Он вступил в лучший шахматный клуб города, где обнаружил, к своему удивлению, что способен обыграть любого, кроме самых-самых лучших, и очень нелегко выбрать тех, кого он не может запросто победить. Он обнаружил еще и книжную лавочку, принадлежащую шахматному энтузиасту, где покупал тяжелые тома по теории дебютов и сборники партий. Купленную в Инсбруке шахматную доску он установил на столике перед камином, рядом с удобным глубоким креслом, оббитым мягким бархатом. Там и происходили его ночные встречи с новыми черно-белыми друзьями.

Так было почти две недели. «Две очень счастливые недели», – сказал мне дядя. И счастье становилось глубже от предвкушения восторженного (а как же!) отзыва Харди и Литлвуда на его монографию.

Но когда пришел ответ, ничего восторженного в нем не было, и счастье дяди Петроса увяло на корню. Реакция вообще была не такой, как он себе представлял. В довольно коротком письме Харди сообщал, что первый важный результат, который дядя про себя называл «Теоремой Папахристоса о разложении», был получен два года назад молодым австрийским математиком. Харди даже выражал изумление, что Петрос об этом не знает, поскольку публикация произвела сенсацию в кругах специалистов по теории чисел и принесла громкую славу молодому автору. Разве Петрос не следит за работами в своей области? Что касается второй теоремы, то незадолго до своей смерти в 1920 году Рамануджан сформулировал ее без доказательства в письме к Харди – одно из последних проявлений его гениальной интуиции. В последующие годы Харди и Литлвуд сумели заполнить пробелы, и их доказательство было опубликовано в последнем выпуске «Трудов Королевского Общества» – экземпляр прилагается.

Харди закончил свое письмо на личной ноте, выразив сочувствие Петросу по поводу такого поворота событий. Кроме того, он высказал предположение – со свойственной его нации и классу сдержанностью, – что в будущем Петросу было бы полезнее поддерживать более тесный контакт с коллегами. Если бы Петрос вел нормальную жизнь математика, указывал Харди, посещал международные конгрессы и конференции, переписывался с коллегами, узнавая о ходе их работы и сообщая о ходе своей, он бы не оказался вторым в получении результатов, безусловно, выдающихся. Если же он будет продолжать держать себя в изоляции, подобные «прискорбные обстоятельства» непременно повторятся.

В этот момент мой дядя прервал рассказ. Он говорил уже несколько часов подряд. Темнело, птицы в саду постепенно замолкали, только цикады ритмично трещали в тишине. Дядя Петрос встал, тяжелым шагом прошел к выключателю и зажег свет. Голая лампочка слабо осветила место, где мы сидели. Дядя медленно зашагал обратно в бледно-желтом свете и фиолетовых сумерках и был очень похож на призрака.

– Значит, вот в чем объяснение, – произнес я почти про себя, когда он сел.

– Какое объяснение? – рассеянно спросил он.

Я рассказал ему о Сэмми Эпштейне и его неудачной попытке найти упоминание имени Петроса Папахристоса в указателях работ по теории чисел, если не считать ранних совместных публикаций с Харди и Литлвудом о дзета-функции Римана. Я изложил «теорию перегорания», которую предложил моему другу «уважаемый профессор» нашего университета: что его предполагаемые занятия проблемой Гольдбаха были всего лишь маскировкой для бездеятельности.

Дядя Петрос горько рассмеялся.

– О нет! Ничего подобного не было, любимейший из племянников! Можешь сказать своему другу и его «уважаемому профессору», что я действительно работал над проблемой Гольдбаха – и как работал, и сколько работал! Да, я получал промежуточные результаты – результаты замечательные и важные, – но не опубликовал их, когда должен был, и меня опередили другие. К сожалению, в математике серебряных медалей не дают. Анонс, а потом публикация – вот что приносит славу. Все остальное – ноль. – Дядя помолчал. – Как говорит пословица, синица в руках лучше, чем журавль в небе, а я, погнавшись за журавлем, упустил синицу…

– Дядя Петрос, – спросил я, – ты, наверное, до смерти огорчился, получив письмо Харди?

– Конечно, огорчился, и «до смерти» – совершенно правильное выражение. Я был в отчаянии, меня одолевали злость, досада, мелькнула даже мысль о самоубийстве. Но это было тогда, в другое время. И я был другой. Теперь, оценивая жизнь в ретроспективе, я не жалею ни о сделанном, ни о не сделанном.

– Не жалеешь? То есть ты не жалеешь об упущенной возможности стать знаменитым, получить признание как великий математик?

Он предостерегающе поднял палец:

– Как очень хороший математик, но не великий! Я доказал две хорошие теоремы, и это все.

– Но это же большое достижение!

Дядя Петрос покачал головой:

– Успех в жизни нужно мерить по поставленным целям. Каждый год во всем мире публикуются десятки тысяч новых теорем, но лишь горсть теорем за целое столетие творит историю.

– Но ведь ты говорил, дядя, что это были существенные теоремы.

– Посмотри на этого молодого человека, – сказал дядя, – на австрийца, который опубликовал мою – я все равно ее еще мысленно так называю – теорему о разложениях. Разве этот результат поставил его на пьедестал рядом с Гильбертом или Пуанкаре? Ничего подобного! Может, он забил себе нишу в галерее портретов в цокольном этаже здания Математики… но что из того? Или, например, Харди и Литлвуд. Да, им принадлежит целый зал в этом здании – и очень большой зал, не спорю, – но даже они не воздвигли себе статуй у главного входа рядом с Евклидом, Архимедом, Ньютоном, Эйлером, Гауссом… Вот что было моей единственной целью, и ничего, кроме решения проблемы Гольдбаха, глубокого проникновения в тайны простых чисел, не привело бы меня туда…

У него заблестели глаза – глубоко, направленно, – и он закончил:

– Я, Петрос Папахристос, никогда не опубликовавший ни одного значительного результата, войду в историю математики – точнее, не войду в нее, как человек, ничего не достигший. И это мне подходит. Я не сожалею. Середина меня бы никогда не устроила. Этому эрзацу, бессмертию в сноске, я предпочитаю мой сад, мои цветы, мои шахматы, тот разговор, который у нас с тобой сегодня. Полное забвение!

При этих словах воскресло мое подростковое обожание Идеального Романтического Героя, но сейчас оно было скомпенсировано изрядной дозой реализма.

– То есть, дядя, вопрос стоял так: «все или ничего»?

Он медленно кивнул:

– Можно сформулировать и так.

– И это был конец твоего творческого пути? Больше ты уже не возвращался к проблеме Гольдбаха?

Он поглядел на меня удивленно:

– Возвращался, конечно! На самом деле именно после этого я сделал всю основную работу. – Он улыбнулся. – Мы до этого еще дойдем, мой мальчик. Не беспокойся, в истории моей жизни не будет ignorabimus [19]!

И он вдруг громко рассмеялся собственной шутке – слишком громко, подумалось мне. Потом наклонился ко мне и, понизив голос, спросил:

– Ты посмотрел теорему Гёделя о неполноте?

– Посмотрел, – ответил я, – но не понимаю, какое она имеет отношение к…

Он резко поднял руку, обрывая мою речь.

– «Wir mussen wissen, wir werden wissenf In der Mathematik gibt es kein ignorabimus», – произнес он отчетливо и так громко, что голос его эхом отразился от сосен и вернулся зловеще, как голос призрака. Предположение Сэмми о безумии мгновенно мелькнуло у меня в голове. Может быть, воспоминания усилили его болезнь? Может быть, дядя невменяем?

Мне стало легче, когда он добавил более нормальным голосом:

– «Мы должны знать, мы будем знать! В математике нет ignorabimus!» Так сказал великий Давид Гильберт на международном конгрессе в 1900 году. Объявление математики небесами Абсолютной Истины. Философия Евклида, философия Непротиворечивости и Полноты…

Дядя Петрос вернулся к своему рассказу.

Философией Евклида было преобразование случайного собрания наблюдений над числами и геометрическими фигурами в хорошо организованную систему, где, взяв за основу принятые априори элементарные истины, можно с помощью логических операций, шаг за шагом прийти к строгому доказательству всех истинных утверждений. Математика – как дерево с сильными корнями (Аксиомы), могучим стволом (Строгое Доказательство) и вечно растущей кроной, расцветающей чудесными цветами (Теоремы). Все математики следующих времен – геометры, алгебраисты, специалисты по теории чисел, и более поздние – аналитики, специалисты по алгебраической геометрии, теории групп и т.д., работники всех математических дисциплин, возникающих до сего дня (новые ветви все того же дерева) – никогда не отклонялись от курса великого пионера: Аксиомы – Строгое Доказательство – Теоремы.

С горькой улыбкой Петрос вспомнил проповеди Харди насчет гипотез, обращенные ко всем (особенно к бедняге Рамануджану, который их рождал, как плодородная почва рождает траву): не приставать к нему с гипотезами. «Доказывайте! Доказывайте!» Харди любил говорить, что если бы для благородного рода математиков понадобился геральдический девиз, ничего нельзя было бы придумать лучше этого: «Quod Erat Demonstrandum» [20].

В 1900 году на Втором международном конгрессе математиков в Париже Гильберт объявил, что настало время довести древнюю мечту до ее окончательных следствий. В настоящий момент у математиков есть язык формальной логики, которого не было у Евклида, и этот язык позволяет изучать строгим образом саму математику. Следовательно, святая троица Аксиомы – Строгое Доказательство – Теоремы должна быть применена не только к числам, фигурам или алгебраическим сущностям различных математических теорий, но и к самим теориям. Математики могут наконец строго доказать то, что в течение двух тысячелетий было их главным кредо, не подвергаемым сомнению, центром всего взгляда на математику: а именно, что в математике любое истинное утверждение доказуемо.

Через несколько лет Рассел и Уайтхед выпустили свой монументальный труд «Principia Mathematica», впервые предложив абсолютно строгий способ рассуждений о дедукции: теорию доказательств. И хотя это новое средство много обещало в смысле окончательного ответа на вызов Гильберта, двум английским логикам не удалось фактически доказать критическое свойство. Полнота математических теорий (то есть тот факт, что в них любое истинное утверждение доказуемо) еще не была доказана, но уже ни у кого не оставалось ни малейших сомнений ни в уме, ни в сердце, что когда-нибудь – и очень скоро – такое доказательство появится. Математики продолжали верить, как верил Евклид, что обитают в Царстве Абсолютной Истины. Победный клич, произнесенный на Парижском конгрессе – «Мы должны знать, мы будем знать, в математике нет ignorabimus», - составлял предмет нерушимой веры любого работающего математика.

Я перебил это увлеченное историческое отступление:

– Дядя, я это все знаю. Раз ты заставил меня ознакомиться с теоремой Гёделя, то очевидно, что я знаю и её предысторию.

– Это не предыстория, – поправил меня дядя, – а психология. Ты должен понять тот эмоциональный климат, в котором работали математики в те счастливые дни до Курта Гёделя. Ты меня спросил, как я набрался духу продолжать работу после такого огромного разочарования. Так вот как это было…

Несмотря на то что дядя еще не смог достичь своей цели и решить проблему Гольдбаха, он твердо верил, что эта цель достижима. И вера его, как духовного внука Евклида, была абсолютна. Так как утверждение Проблемы почти наверняка верно (в этом никто всерьез не сомневался, если не считать Рамануджана с его неясным «предчувствием»), ее доказательство где-то существует в каком-то виде. Дядя пояснил примером:

– Представь себе, что твой друг куда-то засунул в доме ключ и просит тебя помочь его найти. Если ты веришь, что память его не подводит, и абсолютно доверяешь его честности, что это значит?

– Это значит, что он действительно потерял ключ где-то в доме.

– А если он тебя еще и заверяет, что больше никто в дом не входил?

– То мы можем предположить, что ключ не был вынесен из дома.

– Эрго [21]?

– Эрго, ключ находится в доме, и после достаточно долгих поисков – в предположении, что дом конечен, – мы его рано или поздно найдем.

Дядя зааплодировал.

– Превосходно! Именно эта уверенность питала мой возрожденный оптимизм. Когда первое потрясение прошло, я однажды утром поднялся и сказал себе: «Какого черта – ведь доказательство же где-то есть!»

– И что?

– И то, мой мальчик, что если доказательство существует, то кому-то суждено его найти!

Это рассуждение до меня не дошло.

– Я не вижу, чем это тебя утешило, дядя Петрос. Из того факта, что доказательство существует, никак не следует, что именно тебе суждено его найти.

Он поглядел на меня так, словно я не заметил очевидного:

– А кто во всем мире был лучше подготовлен для этого, чем я, Петрос Папахристос?

Вопрос был явно риторический, и потому я не потрудился на него ответить. Но был озадачен. Тот Петрос Папахристос, о котором он говорил, был совсем не тем застенчивым и отстраненным пожилым садоводом, которого я знал с детства.

Конечно, потребовалось время, чтобы оправиться после письма Харди и сокрушительных новостей. Но дядя в конце концов оправился. Он собрался с духом, наполнил свои резервуары надежды верой в то, что «доказательство где-то существует», и возобновил поиск, но был уже немного другим человеком. Его неудачное приключение, обнажив в маниакальном стремлении элемент тщеславия, создало у него внутреннее ядро покоя, ощущение того, что жизнь продолжается независимо от проблемы Гольдбаха. Режим его работы стал слегка менее напряженным, и его уму помогали шахматные интерлюдии; разум стал более спокоен, несмотря на постоянную работу мысли.

Кроме того, переход к алгебраическому методу (он уже решил это в Инсбруке) принес ему ощущение радости от начатой заново работы, опьянение от входа в неисследованные земли.

После статьи Римана в середине девятнадцатого века в течение ста лет в теории чисел доминировала аналитическая тенденция. Возвращаясь теперь к древнему элементарному подходу, мой дядя шел в авангарде стратегического отступления, если мне будет позволен такой оксюморон. История математики запомнит его хотя бы за это, если больше будет не за что.

Здесь следует подчеркнуть, что в контексте теории чисел слово «элементарно» ни в коем случае не может считаться синонимом слова «просто» и уж тем более «легко». Методы элементарного подхода – это методы, которыми получены величайшие результаты Диофанта, Евклида, Ферма, Гаусса и Эйлера, и элементарны они лишь в том смысле, что выведены из элементов математики, основных арифметических операций и методов классической алгебры действительных чисел. Несмотря на эффективность аналитического подхода, элементарные методы стоят ближе к фундаментальным свойствам целых чисел, и полученные с их помощью результаты для математика интуитивно яснее и глубже.

Из Кембриджа пошли слухи, что Петросу Папахристосу из Мюнхенского университета не повезло, когда он задержал публикацию важных результатов. Коллеги по теории чисел стали интересоваться его мнением. Его начали приглашать на семинары, которые он с той поры стал непременно посещать, разнообразя поездками свою монотонную жизнь. Просочились также новости (это уже спасибо декану факультета), что он работает над известной своей трудностью проблемой Гольдбаха, и это заставляло коллег смотреть на него со смешанным чувством уважения и сочувствия.

На одной международной конференции примерно через год после возвращения Петроса в Мюнхен он столкнулся с Литлвудом.

– Все работаете над Гольдбахом, старина?

– Все работаю.

– Правду я слышал, что вы используете алгебраический метод?

– Правду.

Литлвуд высказал сомнение, и Петрос сам удивился, что может свободно говорить о содержании своей работы.

– В конце концов, Литлвуд, – заключил он, – никто лучше меня не знает этой проблемы. Интуиция мне подсказывает, что истина, выраженная этой гипотезой, настолько фундаментальна, что ее может открыть лишь элементарный подход.

Литлвуд пожал плечами:

– Я уважаю вашу интуицию, Папахристос; я только говорю, что вы полностью изолировались. Без постоянного обмена идеями вы можете начать гоняться за призраками, сами того не зная.

– Так что вы рекомендуете? – пошутил Петрос. – Публиковать еженедельный отчет о ходе моей работы?

– Послушайте, – серьезно ответил Литлвуд. – Вам надо найти несколько человек, чьему мнению вы доверяете и в чьей честности не сомневаетесь. Начните делиться идеями, обмениваться мыслями, старина!

Чем больше дядя думал над этим предложением, тем больше находил в нем смысла. К собственному удивлению, он понял, что перспектива обсуждать ход своей работы не только не пугает его, но даже наполняет приятным предвкушением. Если говорить о людях, «чьему мнению он доверяет и в чьей честности не сомневается», то это с необходимостью означает аудиторию из двух человек: Харди и Литлвуда.

Он возобновил переписку с ними, которую прервал года через два после отъезда из Кембриджа. Не тратя много слов, он забросил удочку насчет своего намерения провести семинар, на котором он представит свою работу. Незадолго до Рождества 1931 года он получил официальное приглашение провести следующий год в Тринити-колледже. Он знал, что, поскольку с любой практической точки зрения он очень долго отсутствовал в математическом мире, Харди пришлось употребить все свое влияние, чтобы организовать приглашение. Благодарность вместе с радостью предвкушения плодотворного обмена мнениями с двумя великими специалистами по теории чисел заставила его немедленно это приглашение принять.

Первые несколько месяцев в Англии во время 1932-1933 учебного года Петрос описывает как, быть может, самое счастливое время своей жизни. Воспоминания о первом пребывании там пятнадцатью годами раньше вернули его дням в Кембридже энтузиазм молодости, не отравленный возможностью неудачи.

Вскоре после прибытия он представил Харди и Литлвуду очерк своей работы с алгебраическим методом на сегодняшний день, и это впервые за десять лет дало ему радость признания среди равных. Несколько утренних заседаний он простоял у доски в кабинете Харди, излагая ход своей работы за три года, прошедшие после отказа от аналитических методов. Его двое «снова-коллег», вначале проявлявшие крайний скепсис, стали видеть в его подходе некоторые преимущества, Литлвуд даже более, чем Харди.

– Вы должны понимать, – говорил ему последний, – что подвергаете себя серьезному риску. Если вы не дойдете на этом методе до конца, то останетесь почти ни с чем. Промежуточные результаты о делимости, хотя и очень красивые, сейчас уже мало кого интересуют. Если вы не убедите людей, что этим методом можно доказывать важные теоремы, такие, как гипотеза Гольдбаха, то сам по себе метод будет немногого стоить.

Петрос, как всегда, ответил, что осознает риск.

– И все же что-то говорит мне, что вы, быть может, на правильном пути, – обнадежил его Литлвуд.

– Да, – буркнул Харди, – только поторопитесь, Папахристос, пока у вас ум не начал распадаться, как у меня. Помните, в ваши годы Рамануджан был уже пять лет как мертв.

Первый доклад был сделан в начале осеннего семестра, и за готическими окнами кружились желтые листья. В последовавшие зимние месяцы работа дяди двигалась, как никогда раньше. Это было время, когда он стал применять также метод, именуемый им «геометрическим».

Он начал с представления всех составных (т.е. не простых) чисел в виде точек в прямоугольниках, где наименьший простой делитель был шириной, а частное от деления числа на него – высотой. Например, число 15 представлялось в виде прямоугольника 3 х 5, 25 – как 5 х 5, 35 – как 5x7:

С помощью такого метода все четные числа представлялись в виде пар столбцов, как 2 х 2, 2 х 3, 2 х 4, 2 х 5 и т.д.

Напротив, простые числа, как не имеющие целых делителей, представлялись в виде одной строки, например 5, 7, 11:

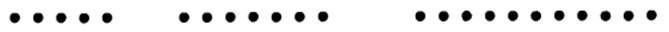Петрос использовал свою геометрическую интуицию для получения теоретико-числовых выводов.

После рождественских каникул он представил свой первый результат. Поскольку, однако, он вместо карандаша и бумаги выкладывал узоры из бобов на полу кабинета Харди, его новый подход вызвал насмешливые дифирамбы Литлвуда. Хотя более молодой член содружества и признал, что «знаменитый метод бобов Папахристоса» до некоторой степени полезен, Харди откровенно был раздражен.

– Что вы придумали с этими бобами? – спросил он. – Между элементарным и инфантильным разница огромная… И не забывайте, Папахристос, эта чертова проблема трудна – а то бы Гольдбах сам ее решил.

Петрос тем не менее верил в свою интуицию, а реакцию Харди отнес на счет «интеллектуального запора от старости» (его собственные слова).

– Великие истины жизни просты, – сказал он Литлвуду за чаем. Литлвуд возражал, вспоминал крайне сложное доказательство теоремы Адамара и Валле-Пуссена о распределении простых чисел. А потом предложил:

– Старина, а что вы скажете насчет того, чтобы заняться настоящей математикой? Я тут работаю над десятой проблемой Гильберта – разрешимость диофантовых уравнений. У меня есть идея, которую хочется проверить, но боюсь, мне нужна помощь с алгеброй. Как вы насчет помочь?

Но Литлвуду пришлось искать помощь с алгеброй в другом месте. Как бы ни был Петрос польщен верой в него коллеги, он решительно отказался. Он слишком погрузился в проблему Гольдбаха, сказал он, врос в нее, чтобы плодотворно работать над чем бы то ни было другим.

Его вера, подкрепленная упрямой интуицией, в «инфантильный» (как сказал Харди) геометрический подход, была так сильна, что впервые со времени начала работы над Проблемой он чувствовал, что находится на волосок от решения. Были даже восторженные минуты в один солнечный январский день, когда ненадолго возникла иллюзия, что он его нашел – но, увы, более трезвый анализ обнаружил небольшую, но решающую ошибку.

(Здесь, дорогой читатель, я должен сознаться: в этот момент дядиного рассказа я невольно ощутил прилив мстительной радости. Я вспомнил то лето в Пилосе, когда тоже какое-то время думал, что решил проблему Гольдбаха – хотя тогда и не знал ее названия.)

Несмотря на глубокий оптимизм, приступы сомнения в себе, иногда на грани отчаяния (особенно после пренебрежительного отзыва Харди о геометрическом методе), стали сильны, как никогда. Дядя боролся с ними, убеждая себя, что это страдания, предшествующие великому триумфу, родовые муки великого открытия. Ведь и ночь темнее всего перед рассветом. Петрос был уверен, что более чем готов для финального рывка. Решительный приступ сосредоточенных усилий – только это и нужно, чтобы вознаградить его последним блестящим озарением.

И потом – славный финиш…

Провозвестие сдачи Петроса Папахристоса, прекращения его усилий решить проблему Гольдбаха пришло во сне, который привиделся ему в Кембридже вскоре после Рождества, – знамение, все значение которого он не сразу постиг.

Как и многие математики, долго работающие над основными арифметическими проблемами, Петрос «подружился с натуральными числами», то есть приобрел глубокое знание пристрастий, капризов и странностей многих конкретных чисел. Несколько примеров: «друг натуральных чисел» сразу распознает 199, 457 или 1009 как простые числа. Число 220 немедленно ассоциируется с числом 284, поскольку эта пара связана необычным соотношением (сумма целых делителей каждого из них равна другому). Число 256 он тут же прочтет как 2 в восьмой степени, вслед за которым идет число, представляющее большой исторический интерес, поскольку 257 может быть выражено в виде

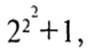а существовала знаменитая гипотеза, что числа вида

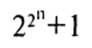являются простыми [22].

Первым известным моему дяде человеком, у которого это качество присутствовало, причем в крайней степени, был Сриниваса Рамануджан. Петрос видел это много раз и даже рассказал мне такую историю [23]:

Однажды в 1918 году они с Харди навещали Рамануджана в санатории. Чтобы сломать лед, Харди сообщил, что номер такси, которое их сюда привезло, был 1729 – число «довольно скучное», как ему показалось. Но Рамануджан, задумавшись лишь на мгновение, энергично возразил: «Нет, Харди, вы неправы! Это очень интересное число – оно наименьшее, которое может быть представлено в виде суммы двух кубов двумя способами!» [24]

За годы, которые Петрос работал над Проблемой с помощью элементарного подхода, его собственная дружба с числами развилась до исключительных пределов. Числа переставали быть неодушевленными сущностями; они почти оживали, у каждого была своя личность. Это – вместе с уверенностью, что решение где-то существует – поддерживало его в самые суровые времена: работая с натуральными числами, он – я цитирую – «чувствовал себя среди друзей».

Эта близость вызывала вхождение некоторых чисел в дядины сны. Из безымянной и безликой массы натуральных чисел, громоздившейся ранее в ночных спектаклях, стали выделяться отдельные актеры, даже главные действующие лица. Например, число 65 являлось почему-то в виде джентльмена из Сити, в котелке и с зонтиком, и с ним всегда один из его простых делителей – 13, гоблиноподобное создание, гибкое и быстрое как молния. Число 333 было жирным лентяем, ворующим куски изо рта своих братьев 222 и 111, а число 8191, известное как «простое число Мерсенна», неизменно имело внешность парижского гамена, вплоть до прилипшей к губе сигареты «голуаз».

Иногда видения были приятны и забавны, иногда безразличны, иногда же назойливы и неприятны. Но была еще одна категория арифметических снов, которые можно было бы назвать только кошмарными, если не из-за ужаса или муки, то из-за глубокой, бездонной тоски. Некоторые четные числа являлись в виде пары близнецов-двойняшек (напомним, что четное число всегда представимо в виде 2k, то есть суммы двух равных целых чисел). Эти близнецы смотрели на дядю не отрываясь, без выражения на неподвижных лицах. Но в глазах их была огромная, хоть и немая боль, боль отчаяния. Если бы они могли говорить, слова были бы такими: «Приди, умоляем тебя! Скорее освободи нас!»

В этих печальных видениях была одна вариация, которая пришла к нему как-то ночью в конце января 1933 года. Это и был тот сон, который дядя ретроспективно назвал «герольдом поражения».

Ему приснилось число 2¹⁰⁰ (2 в сотой степени – число огромное) в виде двух одинаковых веснушчатых темноглазых красавиц, и они глядели прямо на него. Но теперь в этих глазах была не просто грусть, как раньше в глазах Четных, там была злость, даже ненависть. Они смотрели на него долго-долго (уже одного этого было бы достаточно, чтобы назвать сон кошмаром), и потом одна из них мотнула головой из стороны в сторону движением коротким и резким. Рот ее исказился в злобной ухмылке – это была злоба отвергнутой любви.

– Ты никогда до нас не доберешься, – прошипела она.

От этих слов Петрос вскочил с кровати в холодном поту. Слова 2⁹⁹ (то есть половины от 2¹⁰⁰) могли значить только одно: ему не суждено решить Проблему. Конечно, он не был суеверен, как старуха, слепо верящая в приметы. Но глубокое истощение от многих бесплодных лет начало брать свое. Нервы были уже не так крепки, как раньше, и сон его необычайно расстроил.

Не в силах заснуть снова, он вышел погулять по темным туманным улицам, пытаясь стряхнуть ужасную подавленность. Когда он шел в занимающемся рассвете мимо древних каменных зданий, сзади внезапно послышались приближающиеся шаги, и Петрос, охваченный мгновенным страхом, резко обернулся. Из тумана материализовался быстро бегущий молодой человек в спортивной одежде. Он на ходу поздоровался и снова исчез, и его ритмичное дыхание быстро растаяло в тишине.

Все еще расстроенный кошмаром, дядя Петрос не знал точно, наяву ли он увидел этот образ или в мире своих снов. Но когда молодой человек через несколько месяцев вошел к нему в комнату в Тринити-колледже с судьбоносной миссией, дядя сразу узнал рассветного бегуна. Когда вестник ушел, он понял задним числом, что их первая встреча на рассвете была темным предупреждением, таким же, как видение 2¹⁰⁰ – вестью поражения.

Роковой разговор произошел через несколько месяцев после мимолетной рассветной встречи. Этот день отмечен в дневнике дяди Петроса лаконичным комментарием – первым и последним обращением к религии, который я нашел в его дневниках:

17 марта 1933 года. Теорема Курта Гёделя. Святая Мария, Матерь Божия, смилуйся надо мной!

Был конец дня. Дядя весь день пробыл у себя, склонившись в кресле и рассматривая выложенные на полу прямоугольники бобов, уйдя в свои мысли, когда в дверь постучали.

– Профессор Папахристос?

Появилась белокурая голова. У Петроса была хорошая зрительная память, и он сразу узнал молодого бегуна, который рассыпался в извинениях, что побеспокоил.

– Вы меня простите ради Бога за такое вторжение, – сказал молодой человек, – но мне отчаянно нужна ваша помощь.

Петрос сильно удивился – он считал, что его присутствие в Кембридже мало кем замечено. Он не был знаменит, не был даже известен и, если не считать его почти ежевечерних посещений шахматного клуба, ни с кем, кроме Харди и Литлвуда, не обменялся и двумя словами.

– Моя помощь – в чем?

– А, в расшифровке трудного немецкого текста – математического текста. – И молодой человек снова пустился в извинения, что растрачивает время профессора на такие мелочи. Но эта статья так для него важна, и, когда он услышал, что в Тринити-колледже есть его старший коллега из Германии, он не мог удержаться и не попросить его помощи в этом крайне необходимом ему переводе.

В его манере было что-то настолько подкупающее детское, что профессор Папахристос не смог ему отказать.

– Буду рад вам помочь, если это в моих силах. Из какой области статья?

– Формальная логика, профессор. Grundlagen, основания математики.

Петрос был рад услышать, что не из теории чисел, – он было испугался, что молодой коллега хочет выпытать секреты его работы над Проблемой, использовав статью как предлог. Поскольку Петрос уже более или менее закончил свою дневную работу, он предложил молодому посетителю кресло.

– Как, вы сказали, вас зовут? Алан Тьюринг, профессор. Я студент. Тьюринг протянул ему журнал со статьей, открытый на нужной странице.

– A, «Monatshefte fur Mathematik und Physik», сказал Петрос. – «Ежемесячный обзор математики и физики» – издание весьма почтенное. Так, название статьи, как я вижу, «Uber formal unentscheidbare Satce der Principia Mathematica und verwandter Systeme». В переводе это будет… так, минутку… «О формально неразрешимых предложениях Principia Mathematica и аналогичных систем». Автор – некто Курт Гёдель из Вены. Это известный в своей области математик?

Тьюринг поднял на дядю удивленные глаза.

– Разве вы никогда не слышали об этой статье, профессор?

Петрос улыбнулся:

– Дорогой мой, математика тоже заражена этой современной чумой – сверхспециализацией. Боюсь, что понятия не имею о современных достижениях формальной логики, да и других областей математики, если на то пошло. Увы, за пределами теории чисел я полный профан.

– Но, профессор, – возразил Тьюринг, – теорема Гёделя интересна всем математикам, а специалистам по теории чисел – особенно! Ее первые приложения относились к самым основам арифметики, аксиомам Пеано-Дедекинда.

К полному изумлению Тьюринга, Петрос и об аксиомах Пеано-Дедекинда имел довольно смутное представление. Как и любой работающий математик, он считал формальную логику – дисциплину, основным предметом которой является сама математика, – занятием с явно раздутой репутацией, если вообще не бесполезным. Бесконечные попытки строгих обоснований и пересмотра основных принципов он воспринимал как пустую трату времени. Его отношение к этим вопросам лучше всего иллюстрировала народная мудрость «не чини то, что не сломано». Дело математика – доказывать теоремы, а не постоянно жевать мысли о состоянии их невысказанных и не подвергаемых сомнению основ.

Но горячность, с которой говорил молодой посетитель, возбудила любопытство дяди Петроса.

– А что такое доказал этот юный мистер Гёдель, что представляет интерес для теории чисел?

– Он решил проблему полноты, – доложил Тьюринг с горящими глазами.

Петрос улыбнулся. Проблема полноты – не что иное, как стремление формально доказать, что все истинные утверждения в конце концов доказуемы.

– Это хорошо, – вежливо согласился Петрос. – Я вам должен сказать тем не менее – никак не желая оскорбить мистера Гёделя, конечно, – что для работающего ученого полнота математики всегда была очевидной. Все же приятно знать, что кто-то наконец сел и ее доказал.

Но Тьюринг уже неистово мотал головой, и лицо его раскраснелось от возбуждения.

– Вот в том-то и дело, профессор Папахристос! Гёдель ее не доказал!

Петрос не понял.

– Извините, мистер Тьюринг… Вы только что сами сказали, что этот молодой человек решил проблему полноты? Я ведь не ослышался?

– Да, профессор, но вопреки ожиданиям всех – в том числе Гильберта и Рассела – он ее решил в отрицательном смысле! Он доказал, что арифметика и все математические теории не полны!

Петрос не настолько был знаком с концепциями формальной логики, чтобы сразу оценить все вытекающие следствия.

– Простите?

Тьюринг опустился на колени рядом с креслом Петроса и стал тыкать пальцами в хитросплетения символов в статье Гёделя.

– Вот: этот гений доказал – окончательно доказал! – что какие бы аксиомы ни принять, теория чисел с необходимостью будет содержать недоказуемые предложения!

– То есть, вы хотите сказать, ложные предложения?

– Нет, я хочу сказать – истинные предложения; истинные, но такие, которые невозможно доказать!

Петрос вскочил на ноги.

– Это невозможно!

– Но это так, и доказательство тому здесь, на этих пятнадцати страницах: «Истина не всегда доказуема»!

У моего дяди внезапно закружилась голова.

– Но этого… этого не может быть!

Он принялся лихорадочно листать журнал, пытаясь сразу постигнуть изощренные рассуждения статьи, и бормотал про себя, начисто забыв о молодом человеке:

– Мерзость… аномалия… извращение… Тьюринг довольно улыбнулся.

– Все математики поначалу так реагируют. Но Рассел и Уайтхед проанализировали доказательство Гёделя и объявили его безупречным. На самом деле они употребили слово «совершенство».

– «Совершенство»? – скривился Петрос. – Но если он это доказал – то есть действительно доказал, во что я отказываюсь верить, то это – конец математики!

Много часов Петрос пропотел над кратким, но донельзя насыщенным текстом. Он переводил, а Тьюринг объяснял незнакомые ему концепции формальной логики, лежащие в основе рассуждений Гёделя. Закончив перевод, они снова начали сначала, разбирая доказательство шаг за шагом. Петрос отчаянно искал погрешность в рассуждениях.

Это стало началом конца.

Было уже за полночь, когда Тьюринг ушел. Петрос не мог заснуть. Первое, что он сделал утром – пошел к Литлвуду. К его величайшему удивлению, тот уже знал теорему Гёделя о неполноте.

– И как же вы могли ни разу о ней не сказать? – спросил его Петрос. – Как вы можете знать о существовании чего-то подобного и быть таким спокойным?

Литлвуд не понял.

– А чего вы так расстроились, старина? Гёдель изучает некоторые весьма специальные случаи, он ищет парадоксы, очевидно, присущие всем аксиоматическим системам. Какое до этого дело нам, окопным солдатам математики?

Но Петроса нельзя было так легко успокоить.

– Как вы не понимаете, Литлвуд? Отныне, встречаясь с каждым до сих пор не доказанным утверждением, мы должны будем спрашивать себя, а не является ли оно случаем применимости теоремы Гёделя. Ведь любая нерешенная проблема, любая недоказанная гипотеза могут быть априори нерешаемы и недоказуемы! Слова Гильберта «В математике нет ignorabimus» более не применимы. Саму почву, на которой мы стояли, вышибли у нас из-под ног! Литлвуд пожал плечами.

– Не вижу смысла расстраиваться из-за парочки недоказуемых истин, если есть миллионы доказуемых, с которыми можно работать.

– Да, черт побери, но как узнать, кто из них кто?

Хотя реакция Литлвуда должна была бы успокоить – нота оптимизма после катастрофы вчерашнего вечера, – она не дала Петросу ответа на единственный, отравляющий, пугающий вопрос, который возник сразу, как он услышал о результате Гёделя. Вопрос этот был так ужасен, что дядя еле отваживался его сформулировать: что, если теорема Гёделя о неполноте применима к его задаче? Что, если утверждение проблемы Гольдбаха недоказуемо?

От Литлвуда он пошел прямо к Алану Тьюрингу в его колледж и спросил, есть ли продолжающие работы по теореме Гёделя о неполноте. Тьюринг не знал. Было ясно, что только один человек на свете может ответить на его вопрос.

Петрос послал Харди и Литлвуду записку, что некое срочное дело заставляет его ехать в Мюнхен, и в тот же вечер уже был на пароходе, пересекающем Ла-Манш. На следующий день он оказался в Вене. Нужного человека он нашел через знакомых в академических кругах. Они созвонились и, поскольку Петрос не хотел, чтобы его видели в университете, договорились встретиться в кафе отеля «Захер».

Курт Гёдель прибыл точно вовремя – худощавый молодой человек среднего роста, с близорукими глазками за толстыми стеклами очков.

Петрос не стал терять времени.

– Я хочу кое-что у вас спросить, герр Гёдель, причем строго конфиденциально.

Гёдель, стеснительный от природы, почувствовал себя еще более неловко.

– Это личный вопрос, герр профессор?

– Вопрос профессиональный, но относится к моей личной работе, и я был бы очень признателен – нет, я настаиваю! – чтобы это осталось строго между нами. Пожалуйста, сообщите мне, герр Гёдель: существует ли процедура, позволяющая определить, относится ли ваша теорема к какой-либо наперед заданной гипотезе?

Гёдель дал ответ, которого он страшился:

– Нет.

– И на самом деле вы не можете определить априори, какие утверждения доказуемы, а какие нет?

– Насколько мне известно, герр профессор, любое недоказанное утверждение может в принципе быть недоказуемым.

Тут у Петроса перед глазами поплыла красная тьма. Его охватил неудержимый порыв схватить отца теоремы о неполноте за тощую шею и бить головой о блестящую поверхность стола. Но он сдержался, только перегнулся через стол и стиснул руку Гёделя выше локтя.

– Я всю жизнь потратил, пытаясь доказать гипотезу Гольдбаха, – сказал он глухим напряженным голосом, – и теперь вы мне говорите, что она может быть недоказуема?

И без того бледное лицо Гёделя утратило последние краски.

– В теории – да…

– К черту ваши теории! – Головы сидевших в кафе людей повернулись на крик Петроса. – Мне нужно знать точно, можете вы это понять? Я имею право знать, если растратил свою жизнь зря!

Он так сжал пальцы, что Гёдель от боли скривился. Петросу вдруг стало стыдно за свою несдержанность. Как бы там ни было, этот несчастный не отвечает за неполноту математики – он ведь ее только открыл! Петрос разжал руку и промямлил какие-то извинения.

Гёдель дрожал.

– Я п-понимаю ваши ч-чувства, профессор, – выговорил он, – но б-боюсь, что сейчас на ваш вопрос ответить абсолютно невозможно.

С этой минуты смутная угроза, обозначенная теоремой Гёделя о неполноте, стала разворачиваться в неусыпную тревогу и постепенно превратилась в тень, омрачавшую каждый момент жизни Петроса и угасившую в конце концов его боевой дух.

Конечно, это случилось не в один день. Петрос еще несколько лет продолжал свою работу, но это уже был другой человек. Когда он работал, то работал уже только вполсилы, но когда отчаивался, отчаяние было полным, настолько невыносимым, что превращалось в безразличие – чувство, гораздо более терпимое.

– Понимаешь, – объяснил мне Петрос, – когда я услышал эту теорему о неполноте, она сразу разрушила уверенность, которая только и придавала мне силы. Она мне сказала: есть определенная вероятность, что я блуждаю в лабиринте, из которого никогда не найти выхода, пусть даже у меня будет сто жизней, которые я отдам работе. И это по очень простой причине: потому что выхода может не быть, потому что этот лабиринт – бесконечный тупик! О любимейший из племянников, я начал верить, что потратил свою жизнь на погоню за химерой!

Эту новую ситуацию он проиллюстрировал примером, который уже раньше приводил. Предполагаемый друг, который просил его помощи в поиске потерянного в доме ключа, мог страдать амнезией. (Опять-таки мог и не страдать, но не было способа узнать это наверняка.) В этом случае возможно, что «потерянного ключа» вообще никогда и не было!

Утешительной уверенности, на которой строились все его труды двадцати последних лет, более не существовало, и еще больше усиливали тревогу участившиеся посещения Четных Чисел. Теперь они являлись почти каждую ночь, отравляя его сны злой силой. В кошмарах рождались новые образы – постоянные вариации темы неудачи и поражения. Между ним и Четными Числами вырастали высокие стены, и Четные уходили целыми табунами все дальше и дальше, с поникшими головами – разбитая армия, отступающая во тьму пустынных, бесконечных, необъятных просторов… А худшее из всех видений, от которого он всегда просыпался, дрожа, в холодном поту, было 2¹⁰⁰, две веснушчатые темноглазые красавицы. Они глядели молча и пристально, в глазах у них дрожали слезы, и снова и снова их черты поглощала тьма.

Значение сна было ясно, и для истолкования его мрачного символизма не нужны были ни психоаналитик, ни гадалка: увы, теорема о неполноте применима к проблеме Гольдбаха. Это утверждение недоказуемо априори.

Возвратившись в Мюнхен после года в Кембридже, Петрос внешне вернулся и к прежнему образу жизни: преподавание, шахматы и минимум общественной жизни, но, поскольку сейчас ему было нечего делать, он начал иногда принимать случайные приглашения. Впервые с раннего детства оказалось, что погруженность в поиск математических истин не играет в его жизни центральную роль. Хотя он продолжал заниматься своими исследованиями, эти занятия были лишены былого жара. Теперь он отдавал работе не более нескольких часов в день, рассеянно шлифуя свой геометрический метод. Он по-прежнему вставал до рассвета, шел в кабинет и там медленно расхаживал среди выложенных из фасоли прямоугольников (чтобы освободить для них место, он всю мебель сдвинул к стенам). Он где-то добавлял, где-то убирал, что-то про себя рассеянно бормоча. Так проходило некоторое время, а потом, раньше или позже, дядя садился в кресло, вздыхал и переключался на шахматы.

Такой распорядок держался еще года два или три, и время, проводимое за этими «научными занятиями», постепенно сократилось почти до нуля, А потом к концу 1936 года Петрос получил телеграмму от Алана Тьюринга, уже из Принстонского университета:

Я ДОКАЗАЛ НЕВОЗМОЖНОСТЬ АПРИОРНОГО ОПРЕДЕЛЕНИЯ РАЗРЕШИМОСТИ ТЧК

Вот именно: ТЧК. Это значило, в сущности, то, что невозможно заранее узнать, доказуемо ли конкретное математическое утверждение. Если оно в конце концов будет доказано, то оно, очевидно, доказуемо. Тьюрингу удалось показать, что пока утверждение остается недоказанным, абсолютно невозможно утверждать, является оно недоказуемым или просто очень трудным.

Непосредственным следствием этого, касавшимся дяди Петроса, было вот что: если он надумает и дальше искать решение проблемы Гольдбаха, то делать это он будет на свой страх и риск. Чтобы так поступить, нужны два качества – сильный оптимизм и хороший боевой дух. И эти качества у него – от времени, усталости, невезения, из-за Курта Гёделя, а теперь еще и с помощью Алана Тьюринга – истощились.

ТЧК.

Через несколько дней после телеграммы Тьюринга (в дневнике указана дата 7 декабря 1936 года) Петрос сообщил своей домоправительнице, что бобы ему больше не потребуются. Она их собрала, промыла как следует и сварила герру Профессору на обед великолепное мясное ассорти с фасолью.

Дядя Петрос помолчал, удрученно глядя себе на руки. За кругом бледно-желтого света, в котором мы сидели, уже легла полная тьма.

– И вот тогда ты и бросил искать решение? – спросил я тихо.

Он кивнул:

– Да.

– И никогда больше не пытался решать проблему Гольдбаха?

– Никогда.

– А Изольда?

Мой вопрос его, кажется, удивил.

– Изольда? При чем здесь Изольда?

– Я так понял, что Проблемой ты занялся, чтобы завоевать ее сердце?

Дядя Петрос грустно улыбнулся.

– Изольда подарила мне «Дивное странствие», как сказал наш поэт. Без нее я, быть может, «не тронулся бы в путь» [25]. И все же она была всего лишь исходным стимулом. Через несколько лет после начала работы над Проблемой память о ней поблекла, она стала далеким фантазмом, горько-сладким воспоминанием… И мои мотивы оказались более высокого – или возвышенного – сорта. – Он вздохнул: – Бедная Изольда! Она погибла во время бомбежки Дрездена вместе со своими двумя дочерьми. А ее муж, «бравый молодой лейтенант», был убит еще раньше на Восточном фронте.

Последняя часть рассказа моего дяди математического интереса не представляет.

В последующие годы силой, определяющей его жизнь, стала не математика, а история. Мировые события сломали защитный барьер, за которым он счастливо жил в своей башне из слоновой кости. В 1938 году гестапо арестовало его домоправительницу и отправило в лагеря, которые тогда еще называли «трудовыми». Он никого на ее место не нанял, наивно веря, что она скоро вернется, а арест объясняется каким-либо «недоразумением». (Когда война закончилась, он от выживших ее родственников узнал, что домоправительница погибла в 1943 году в Дахау, почти рядом с Мюнхеном.) Он начал питаться в ресторанах, возвращаясь домой только для сна. Почти все свободное от университета время он проводил в шахматном клубе, играя, наблюдая и анализируя партии.

В 1939 году декан математического факультета, к тому времени видный член нацистской партии, указал, что Петросу следует немедленно подать на получение немецкого гражданства и официально стать подданным Третьего Рейха. Петрос отказался не из каких-либо принципов (он сумел пройти по жизни, не неся груза идеологии), но потому, что меньше всего на свете ему хотелось опять заниматься дифференциальными уравнениями. Было ясно, что подавать на гражданство ему предложило министерство обороны, имея в виду именно эту цель. После отказа дядя, по сути, стал persona non grata [26]*. В сентябре 1940 года, незадолго до того, как Италия объявила войну Греции (дядя Петрос сразу оказался бы враждебным иностранцем, подлежащим интернированию), он покинул Германию.

Если судить по строгим критериям публикаций, дядя Петрос уже много лет не был работающим математиком, а потому на академическую должность рассчитывать не мог. Он вернулся на родину. В первые пять лет оккупации Греции странами Оси он жил в семейном доме в центре Афин, на улице Королевы Софии, с недавно овдовевшим отцом и недавно женившимся братом Анаргиросом (мои родители уже переехали тогда в свой дом), почти все свое время посвящая шахматам. Однако очень скоро появились на свет мои кузены, которые сначала орали, а потом начали всюду лазить и досаждали дяде куда больше нацистских и фашистских оккупантов. Он переехал в старый сельский дом в Экали, в котором давно уже никто из семьи не жил.

После освобождения мой дед сумел, дергая за нужные ниточки, добиться для Петроса предложения занять кафедру анализа в Афинском университете. Петрос предложение отклонил под фальшивым предлогом, что «это помешает его работе». (В этом случае теория моего друга Сэмми, что дядя использует проблему Гольдбаха как оправдание для собственной лени, оказалась полностью справедлива.) Через два года после этого патриарх семейства Папахристос умер, оставив своим сыновьям равные доли в бизнесе, а главные руководящие посты – моему отцу и Анаргиросу. «Мой старший сын Петрос, – указал он в завещании, – сохраняет привилегию заниматься своими важными математическими исследованиями», то есть привилегию сидеть на шее у своих братьев, не делая никакой работы.

– А потом что? – спросил я, все еще надеясь на сюрприз, который может ждать где-то на последней странице.

– А потом ничего, – ответил дядя. – Почти двадцать лет моя жизнь шла так, как тебе известно: шахматы и садоводство, садоводство и шахматы. Да, и еще раз в месяц поездка в благотворительное заведение, основанное твоим дедом, чтобы помочь им с бухгалтерией. Это для спасения моей души, если таковая все же существует.

Уже была полночь, и я очень устал. Все же я чувствовал, что должен закончить вечер оптимистической нотой, и, от души зевнув и потянувшись, я сказал:

– Дядя, ты великолепен… если ничем другим, то хотя бы силой духа и величием души, с которыми ты принял поражение.

Но реакцией на мои слова было крайнее удивление.

– О чем ты говоришь? – спросил дядя. – Никакого поражения не было!

Теперь настала моя очередь удивиться.

– Как не было?

– О нет, милый мой мальчик! – Дядя помотал головой. – Я вижу, ты так ничего и не понял. Я не потерпел поражения – мне просто не повезло.

– Не повезло? Не повезло в том смысле, что ты выбрал такую трудную проблему?

– Да нет, – ответил он, удивляясь моей неспособности понять очевидное. – Не повезло – это, кстати, еще очень мягко сказано – выбрать проблему, которая не имеет решения. Разве ты не слушал? – Он тяжело вздохнул. – Постепенно подтвердились мои предположения: проблема Гольдбаха неразрешима!

– Но как ты можешь быть в этом уверен?

– Интуиция, – сказал он, пожав плечами. – Это единственное средство, которым владеет математик, когда нет доказательства. Для истины, столь фундаментальной и столь простой по формулировке и все же столь невообразимо устойчивой против любых систематических рассуждений, есть только одно объяснение. Сам того не зная, я взял на себя сизифов труд. Я нахмурился.

– Ну, я не знаю, – начал я. – Но с моей точки зрения…

Тут дядя Петрос перебил меня громким смехом.

– Может, ты и талантливый мальчик, – сказал он, – но в смысле математики ты пока что еще только эмбрион – а я в свое время был настоящим великаном. Поэтому не стоит противопоставлять твою интуицию моей, о любимейший из племянников!

Против этого мне, конечно, возразить было нечего.