"Лекции по схемотехнике" - читать интересную книгу автора
2.4.1 Расчётный метод минимизации
Применение этого метода состоит в последовательном применении к некоторой формуле законов и правил тождественных преобразований алгебры логики. При этом широко используют следующие приёмы: прибавление одного или нескольких членов, входящих в СДНФ, поскольку X #8744; X #8744; X = X; выделение членов, содержащих множитель
Пример: Минимизировать функцию СДНФ мажоритарного элемента (См. п.2.2) и реализовать его схему на элементах основного базиса.
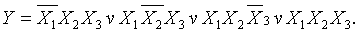 |
Склеивая первые три минтерма с четвёртым, получаем ДНФ функции мажоритарного элемента, которая проще СДНФ:
Минимизированная функциональная схема мажоритарного элемента приведена на рисунке 7.
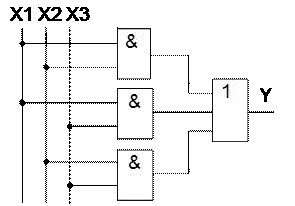 |
Рисунок 7 Функциональная схема мажоритарного элемента, реализованная на основе минимизированной функции ДНФ
Из сравнения схем, приведённых на рисунках 3 и 7 следует, что в минимизированной схеме число по Квайну уменьшилось с 19 до 9.
Карта размечается системой координат, соответствующих значениям входных переменных. Обратим особое внимание на то, что координаты столбцов (а также и строк, если ngt;3), следуют не в естественном порядке возрастания двоичных кодов, а так: 00 01 11 10. Это делается для того, чтобы соседние наборы (в том числе и столбцов 1 и 4) отличались лишь одной цифрой в каком-либо разряде.
Процесс минимизации заключается в формировании правильных прямоугольников, содержащих по 2k ячеек, где k — целое число. В прямоугольники объединяются соседние ячейки, которые соответствуют соседним элементарным произведениям (т. е. отличаются только в одном разряде).
Несмотря на то, что карты Карно изображаются на плоскости, соседство квадратов устанавливается на поверхности тора. Верхняя и нижняя границы карты как бы склеиваются, образуя поверхность цилиндра. При склеивании боковых границ получается поверхность тора.
Пример: Минимизировать функцию трёх переменных, заданную таблицей истинности (таблица 6).
Таблица 6 Таблица истинности функции трёх переменных
| X1 | X2 | X3 | Y |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
СДНФ функции:
Составляем карту Карно и производим разметку её сторон:
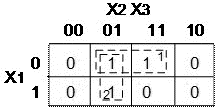 |
Рисунок 8 Карта Карно функции 3-х переменных.
На карте Карно формируем два прямоугольника. Первый из них объединяет (как бы заключает в скобки) два первых минтерма (слагаемых), а второй — первое и третье слагаемые СДНФ минимизируемой функции, приведённой выше. Минтермы, объединённые в прямоугольники, отличаются только в одном разряде. Их неизменяемая часть, которая при минимизации расчётным методом выносится за скобки, и является минимизированным значением функции:
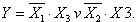 |
1 Изображается карта Карно и производится разметка её сторон.
2 Ячейки карты Карно, соответствующие наборам переменных, обращающих функцию в «1», заполняются единицами, остальные — нулями.
3 Выбирается наилучшее покрытие карты прямоугольниками. Наилучшим считается покрытие, образованное минимальным числом прямоугольников, а если таких вариантов несколько, то выбирается тот, который даёт максимальную площадь прямоугольников.
Пример: Минимизировать функцию четырёх переменных, представленную картой Карно: (Рисунок 9).
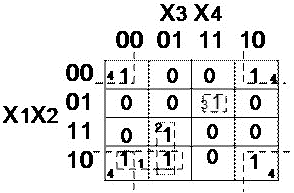 |
Рисунок 9 Карта Карно функции 4-х переменных
Из карты Карно записываем минимизированное значение функции:
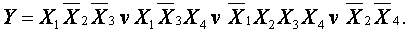 |
| © 2024 Библиотека RealLib.org (support [a t] reallib.org) |