"Windows XP" - читать интересную книгу автора (Виталий Петрович Леонтьев.)
СИСТЕМЫ СЧИСЛЕНИЯ
Человек, как известно, может распознавать тысячи (если не миллионы) видов всевозможных сигналов. Когда мы читаем книгу, минимальным информационным элементом для нас становится буква, цифра или знак препинания. Итого - несколько десятков различных символов! При разговоре же мы должны распознавать уже сотни (если не тысячи) минимальных сигналов - звуки, элементы интонации, мимические и жестовые сигналы.
Нам, людям, это трудным не кажется. Но наш мозг учится искусству понимания этих сигналов долгие годы, методом проб и ошибок переводя внешние сигналы в понятные ему нервные импульсы, несущиеся по нейронным сетям. Эти импульсы и есть основной, изначальный язык мозга.
А как обстоит дело в компьютере? Точно так же - вся поступающая извне информация переводится на самый простой для компьютера язык, язык машинных кодов в двоичной системе.
Числа являются основой не только математики, но и информатики. Невозможно представить работу за компьютером без знания чисел. Кроме того, явно или неявно числа пронизывают всю цивилизацию.
Прежде чем приступать к рассказу о компьютерных числах, вспомним, чем отличается число от цифры. Часто по радио или телевизору можно услышать, что ведущая просит гостя программы - обычно ученого - назвать
При написании и чтении компьютерных книг до такой степени, конечно, расслабляться нельзя. Здесь всегда число - это измеритель некоторого количества, иногда - порядковый номер. А цифры - это всегда значки, которыми записываются числа или с помощью которых произносятся.
Обычных «школьных» цифр всего десять: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. С их помощью можно записать любые числа (количества), но для этого нужно использовать определенные правила, которые всем известны со школы. Так вот, цифры вместе с правилами записи чисел и называются системой счисления.
Вспомним, как записываются эти числа. При записи числа каждая цифра, которая входит в его запись, означает определенное количество. Какое? Давайте посмотрим пример. Возьмем число 4891. Как оно получается из своих цифр? А вот как:
4891 = 4x1000 + 8x100 + 9x10 + 1x1.
Мы видим, что количество, которое несет в себе каждая цифра, зависит от положения, позиции цифры в записи числа. Если цифра стоит на первом месте справа, то ее следует домножить на 1, если на втором месте справа - то на 10, на третьем - на 100 и так далее, пока число не кончится. По этой причине такая система счисления называется позиционной. Вспоминая, что количество цифр «школьной» системы равно десяти, получаем ее полное название - позиционная десятичная система счисления.Количество цифр позиционной системы счисления называется ее основанием. То есть «школьная» система счисления имеет своим основанием десять.
Сделаем еще одно существенное замечание: наш русский язык представляет собой десятичный язык. Все числа, которые мы произносим, составлены по правилам десятичной системы счисления. (Поскольку все системы счисления, с которыми мы будем знакомиться, суть позиционные, слово «позиционная» будем опускать.) С одной стороны, это удобно и привычно, мы даже этого не замечаем. Но, с другой стороны, у нас будут возникать трудности при именовании чисел, записанных в других, недесятичных системах, - просто не будет слов.
Очень важно и то, что цифры умножаются только на степени числа 10. Поэтому наше число можно записать еще и так:
4891 = 4х10^3 + 8х10^2 + 9x10^1 + 1x10^°.
Следует также заметить, что приписывание любой цифры справа от числа меняет число. Например, числа 4, 48, 489, 4891, 48910 - все разные. Приписывание цифры слева также меняет число, но только в случае, если эта цифра - не нуль. Так, числа 0, 10, 910, 8910, 48910 - также все разные. А вот числа 48, 048, 0048, 00048 являются одним и тем же числом - 48. Таким образом, приписывание слева нуля не меняет числа - не меняет количества, которое обозначает число.
Наконец, при знакомстве с другими системами - нам пригодится такое понятие, как количество цифр в числе. Количество цифр в числе - это количество цифр в числе. Однако дело здесь не так просто, как может показаться на первый взгляд. Для начала перечислим все однозначные десятичные числа:
О, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Да, это просто цифры. Но это не означает, что цифра и однозначное число - одно и то же. Цифра - это цифра, то есть знак. А число, пусть даже и однозначное - это количество. Итак, однозначных чисел ровно десять.
Перейдем к двузначным. Какое самое большое двузначное число? Правильно, 99. А самое маленькое? 10? Вот и не угадали. 01? Снова не угадали. На компьютере самое маленькое двузначное число - это 00. И только следом по порядку идет двузначное число 01. Потом - 02 и так далее. Список всех двузначных чисел выглядит так:
00, 01, 02, 03, …, 97, 98, 99.
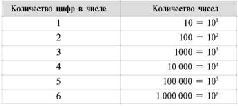
Сколько всего? Правильно, ровно сто. Теперь легко можно догадаться, сколько всего существует трехзначных, четырехзначных и так далее десятичных чисел. Сведем наши знания в следующую таблицу.
 |
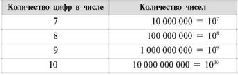 |
Что означает эта таблица? А означает она то, что однозначными числами можно закодировать 10 объектов, двузначными - 100 объектов и так далее. Например, количество автомобильных номеров с одинаковыми буквами и разными цифрами ровно 1000 - ведь автомобильный номер содержит три цифры. Разных телефонных номеров в Москве может быть ровно десять миллионов: каждый телефонный номер состоит из семи цифр (без учета цифр кода города).
Вернемся к «азбуке» информационной науки. Впрочем, азбука ли это? Ведь букв-то как раз здесь и нет, одни цифры - не зря же компьютерные технологии называют еще и «цифровыми». Да и цифр немного - всего две:
¦ 0 - отсутствие сигнала;
¦ 1 - его наличие.
Хорошая азбука, что и говорить! Такую даже первоклассник выучит за секунду. Да только мала - много ли слов составишь из ее «букв»? Немного. Но для компьютера - вполне достаточно. И как же по научному называется такая система счисления из двух цифр? Нетрудно догадаться, что двоичной.
Двоичная система счисления действительно очень простая, даже самая простая. Для подтверждения этой мысли представим таблицы умножения и сложения двоичной системы.
Сначала - таблица умножения.Если вспоминается таблица умножения десятичной системы, забудьте как страшный сон. Мало есть вещей, более простых, чем таблица умножения двоичной системы.
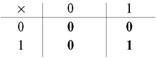 |
Какое в этой таблице самое сложное действие? Конечно, 1x1 = 1. Остальные ее действия - 0x0=0, 0x1=0, 1x0=0 - как говорят математики, абсолютно тривиальны.
Название таблицы сложения произошло, видимо, от слова «сложный». Таблица сложения двоичной системы не просто сложнее таблицы умножения. Она сложна по жизни. Точнее, камень преткновения составляет одно единственное действие, но на нем держится вся система и все компьютеры. Посмотрим на эту «страшную» таблицу сложения:
 |
Вся суть этой таблицы - в ее самом сложном действии: 1 + 1 = 102 «один-ноль». Остальные действия не представляют для нас никакой угрозы: 0 + 0 = 0, 0 + 1 = 1, 1 + 0 = 1. А что это за индекс «два» у числа 10
Какое же количество обозначает это число 10
Другими словами, 10
Для тренировки выпишем первые двоичные числа от 0 до 16. Воспользуемся при этом основным свойством чисел: следующее число больше предыдущего на 1.
0 и 1 можно писать без указания системы счисления: 0 и 1 и в Африке 0 и 1.
Самый эффективный способ получить следующее число - это прибавить один столбиком. Да, да, тем самым «школьным» столбиком. Он прекрасно «работает» в любых системах счисления. Сначала получим:
1 + 1 = 10
10
11
Как нетрудно заметить, главное в этом деле - все время помнить, что один да один будет не два, а «один-ноль». Нуль пишем, один в уме…
Следует иметь в виду: заложенная в русский язык десятичная система ни в коем случае не должна использоваться для называния чисел в других системах.
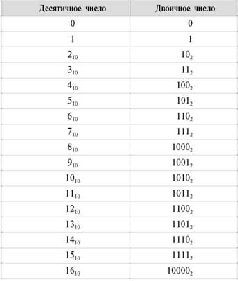
Если продолжить это увлекательное занятие, то получится следующая таблица с первыми 16 двоичными (и десятичными) числами, не считая нуля.
 |
Теперь, имея такую чудную таблицу, займемся важным делом: подсчитаем, сколько же разных слов можно составить из наших цифровых «букв». То есть снова посчитаем количество чисел с одинаковым количеством цифр, но уже в двоичной системе счисления. Только не запутайтесь: подсчет будем вести в десятичной системе.
Итак, изучая эту таблицу, получаем:
¦ 2 однозначных двоичных числа 0 и 1;
¦ 4 = 22 двузначных двоичных числа: 00, 01, 102 и 112;
¦ 8 = 23 трехзначных двоичных чисел от 000 до 1112;
¦ 16 = 24 четырехзначных двоичных чисел от 0000 до 11112.
Уф! Дело сделано. Позволим себе рассуждать по аналогии и, учитывая подобный опыт подсчета количества таких чисел для десятичной системы, получим уникальную таблицу количества всех двоичных чисел, имеющих один знак, два знака, три знака и так далее до десяти знаков.
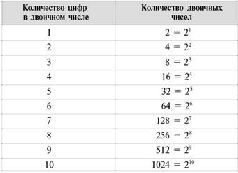 |
Имеют ли «слова», составленные из двоичных цифровых «букв», какие-то специальные названия? Имеют, и весьма значимые.
«Слова», составленные из одной «буквы» - однозначные числа - называются битами. Бит может принимать только два значения - 0 и 1. Бит можно представить как выбор ответа «да» или «нет» на поставленный вопрос. Электронным представлением бита на компьютере является ситуация «есть сигнал / нет сигнала». В математических науках и информатике ответ «да» обычно обозначается цифрой 1, «нет» - цифрой 0. Одним битом можно закодировать два объекта.
«Слова», состоящие из восьми «букв», то есть восьмизначные двоичные числа, называются байтами. Восьмерка здесь присутствует не случайно: это первое мистическое компьютерное число. Откуда взялась в байте именно цифра 8, никто не знает (может быть, по количеству колонн Большого театра в Москве?). Но эта цифра постоянно буквально путается под ногами у компьютера. Позволю себе процитировать по этому поводу очень серьезную книгу американских специалистов, изданную ими в 1985 г.:
То есть размер байта 8 бит устоялся в основном как оптимальный с точки зрения кодирования символов.
Примерами восьмизначных компьютерных «слов» - байтов можно записать следующие числа:
00001111 10101000 10001111 10000110 01010101 и так далее.
В каком же диапазоне изменяются наши 256 байтов? Очевидно, что от 0000 0000 до 1111 1111, при переводе в десятичную систему от 0 до 255.
Не путайте биты с байтами! Бит состоит из одной двоичной цифры, и разных битов всего два: 0 и 1. Байт содержит ровно восемь цифр, не больше и не меньше. А сколько всего имеется разных байтов? Это легко выяснить из предыдущей таблицы: 256.
Получили второе мистическое компьютерное число - 256. Компьютер все время работает с байтами, обычно ими легче оперировать. Но по мере развития прогресса компьютеры становились все мощнее и мощнее, все мозговитее и мозговитее. Байтов в них становилось все больше и больше. Сейчас их уже так много, что разработана целая система так называемых производных единиц от байта.
Короче, сначала придумали третье компьютерное число, равное 2 = 1024. Почему такое? Очень просто. Во-первых, круглая степень - 10. Во-вторых, 1024 почему-то почти равно 1000. А 1000 - это основание для обычных производных единиц: 1 километр равен 1000 метров, 1 килограмм равен 1000 граммов. Дело даже дошло до того, что один немецкий компьютерный журнал поместил изображение 1 киломарки, равной 1024 маркам…
Затем постановили, что 1024 байта равны 1 - правильно! - килобайту.А 1024 килобайта равны 1 мегабайту,и так далее. Все имеющиеся производные единицы байта находятся в следующей таблице.
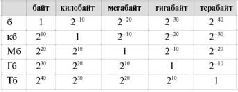 |
Только будьте внимательны при использовании производных единиц! Полностью их имена пишутся с маленькой буквы, а сокращенно - с большой (но байт сокращается до маленькой буквы).
¦ 1 килобайт = 1 кб = 1 К = 210 б;
¦ 1 мегабайт = 1 Мб = 1 М = 210 К = 220 б;
¦ 1 гигабайт = 1 Гб = 1 Г = 210 М = 220 К = 230 б.
Как же перевести число из привычной нам десятичной системы в двоичную?
Проще всего - с помощью инженерного калькулятора. Если же такового под рукой не окажется, можно произвести это преобразование с помощью обычной бумаги и карандаша. Наиболее известный и простой способ перевода из десятичной системы в двоичную производится в десятичной системе путем деления на 2 - на основание двоичной системы. Приведем алгоритм перевода чисел из десятичной системы в двоичную, состоящий из двух шагов.
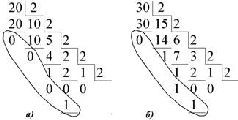
Число в десятичной системе делится на 2. Получаем частное и остаток. Частное снова делится на 2. Снова получаем частное и остаток. Опять делим новое частное на 2 и так далее. Остатки от деления - цифры 0 и 1 - являются цифрами соответствующего двоичного числа, записанными справа налево.
Процесс деления прекращается, когда частное становится равным нулю. В первом случае (а) у нас 20
 |
А наоборот?
Наиболее прост такой способ превращения двоичного числа в десятичное. Подпишем под последней цифрой двоичного числа десятичное число 2° = 1, под второй цифрой справа - число 2
Например:
10101000
 |
010101012 = 6410 + 1610 + 410 + 110= 8510.
 |
Кроме двоичной системы счисления, в компьютерной практике также используется шестнадцатеричная система. На практике она используется даже чаще, чем двоичная: при задании цветов страницы сайта, при доступе к символам современных двухбайтовых шрифтов, при программировании, особенно на ассемблере… Дело в том, что байт кодируется в точности двузначным шестнадцатеричным числом, что гораздо более просто и читабельно, чем в двоичной системе. Но об этом ниже.
В некотором смысле шестнадцатеричная система еще хуже, чем двоичная. Судите сами. Сколько цифр в шестнадцатеричной системе? Ровно 16. И какими же цифрами их обозначать? А вот какими:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С, D, E, F.
Здесь ровно 16 цифр. Последние шесть цифр взяты из латинского алфавита и читаются так:
¦ А - цифра «а». Это цифра «десять»;
¦ В - цифра «бэ» - цифра «одиннадцать»;
¦ С - цифра «цэ» - «двенадцать»;
¦ D - цифра «дэ» - «тринадцать»;
¦ Е - цифра «е» - «четырнадцать»;
¦ F - цифра «эф» - «пятнадцать».
Как видите, проблемы с русским языком стали еще серьезней. Первые шестнадцатеричные числа мы выписывать не будем, а укажем только ключевые моменты получения следующего шестнадцатеричного числа, которых, в отличие от двоичной системы, не один, а уже четыре.
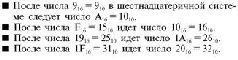 |
Лучше понять шестнадцатеричную систему можно, изучая ее таблицу сложения:
 |
Из шестнадцатеричной системы в десятичную числа переводятся так же, как и из двоичной, только, конечно, нужно делить не на 2, а на 16, а остатки, значения которых будут от О до 15, переводить в шестнадцатеричные цифры. Обратный перевод осуществляется так же, как было представлено десятичное число в начале главы, только в степень возводится число 16. Например:
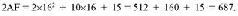 |
Гораздо интереснее переводить двоичные числа в шестнадцатеричные и обратно.
Алгоритм перевода из шестнадцатеричной системы в двоичную такой:
¦ каждая цифра шестнадцатеричной записи числа записывается четырехзначным двоичным числом;
¦ нули, стоящие слева, можно отбросить.
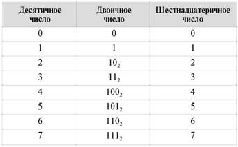
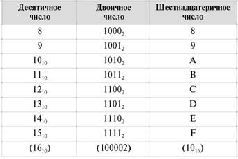
Запись шестнадцатеричных цифр двоичными числами берут из следующей таблицы, в которой везде, где это не может привести к недоразумению, у чисел опущены индексы с основанием системы счисления.
 |
 |
Примеры.
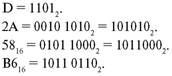 |
Алгоритм перевода из двоичной системы в шестнадцатеричную.
¦Каждые четыре двоичные цифры, считая справа налево, записываются одной шестнадцатеричной цифрой, которые выписываются также справа налево.
¦ Если для последней четверки не хватает цифр, слева от двоичного числа дописываются нули.
Примеры.
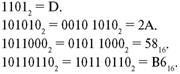 |
| © 2024 Библиотека RealLib.org (support [a t] reallib.org) |