"Элегантная вселенная (суперструны, скрытые размерности и поиски окончательной теории)" - читать интересную книгу автора (Грин Брайан)
Глава 6. Только музыка, или Суть теории суперструн
С давних времен музыка является источником метафорических образов для тех, кто пытается разгадать тайны Вселенной. Начиная с «музыки сфер» древних пифагорейцев и до «гармонии мира», на протяжении столетий направляющих наши научные поиски, мы пытаемся понять песнь природы в величественных хороводах небесных тел и неистовой пляске субатомных частиц. С открытием теории суперструн музыкальные метафоры приобрели удивительную реальность, поскольку согласно этой теории микромир заполнен крошечными струнами, звучание которых оркеструет эволюцию мироздания. Согласно теории суперструн ветры перемен дуют через эолову арфу Вселенной.
В противоположность этому стандартная модель представляет элементарные компоненты мироздания в виде точечных образований, лишенных какой-либо внутренней структуры. Несмотря на необыкновенную мощь (как мы уже упоминали, практически все предсказания стандартной модели о свойствах микромира подтвердились с точностью до одной миллиардной от одной миллиардной доли метра, что представляет собой предел разрешающей способности современной техники), стандартная модель не смогла стать полной или «окончательной теорией», поскольку она не включает гравитационного взаимодействия. Более того, все попытки включить гравитацию в квантово-механическую формулировку этой модели закончились неудачей из-за неистовых флуктуации структуры пространства, проявляющихся на ультрамикроскопических расстояниях, т.е. на расстояниях, меньших планковской длины. Это неразрешенное противоречие явилось побудительным мотивом для поиска более глубокого понимания природы. В 1984 г. физик Майкл Грин, работавший в то время в колледже Королевы Марии, и Джон Шварц из Калифорнийского технологического института впервые представили убедительные доказательства того, что
Теория струн предлагает оригинальное и глубокое изменение теоретического описания свойств Вселенной на ультрамикроскопическом уровне — изменение, которое, как постепенно осознают физики, модифицирует эйнштейновскую общую теорию относительности, делая ее полностью совместимой с законами квантовой механики. Согласно теории струн элементарные компоненты Вселенной
Однако уже простая замена точечных частиц струнами в качестве фундаментальных компонентов мироздания ведет к далеко идущим последствиям. Первое и самое главное состоит в том, что теория струн, по-видимому, разрешает противоречие между общей теорией относительности и квантовой механикой. Как мы увидим ниже, пространственная протяженность струн является новым ключевым звеном, позволяющим создать единую гармоничную систему, объединяющую обе теории. Во-вторых, теория струн действительно представляет объединенную теорию, поскольку в ней все вещество и все взаимодействия обязаны своим происхождением одной фундаментальной величине — колеблющейся струне. Наконец, как будет показано более подробно в последующих главах, помимо этих блестящих достижений, теория струн еще раз радикально изменяет наши представления о пространстве-времени.[45]
В 1968 г. молодой физик-теоретик Габриэле Венециано корпел над осмыслением многочисленных экспериментально наблюдаемых характеристик сильного ядерного взаимодействия. Венециано, который в то время работал в ЦЕРНе, Европейской ускорительной лаборатории, находящейся в Женеве (Швейцария), трудился над этой проблемой в течение нескольких лет, пока однажды его не осенила блестящая догадка. К большому своему удивлению он понял, что экзотическая математическая формула, придуманная примерно за двести лет до этого знаменитым швейцарским математиком Леонардом Эйлером в чисто математических целях — так называемая бета-функция Эйлера, — похоже, способна описать одним махом все многочисленные свойства частиц, участвующих в сильном ядерном взаимодействии. Подмеченное Венециано свойство давало мощное математическое описание многим особенностям сильного взаимодействия; оно вызвало шквал работ, в которых бета-функция и ее различные обобщения использовались для описания огромных массивов данных, накопленных при изучении столкновений частиц по всему миру. Однако в определенном смысле наблюдение Венециано было неполным. Подобно зазубренной наизусть формуле, используемой студентом, который не понимает ее смысла или значения, бета-функция Эйлера работала, но никто не понимал почему. Это была формула, которая требовала объяснения. Положение дел изменилось в 1970 г., когда Йохиро Намбу из Чикагского университета, Хольгер Нильсен из института Нильса Бора и Леонард Сасскинд из Станфордского университета смогли выявить физический смысл, скрывавшийся за формулой Эйлера. Эти физики показали, что при представлении элементарных частиц маленькими колеблющимися одномерными струнами сильное взаимодействие этих частиц в точности описывается с помощью функции Эйлера. Если отрезки струн являются достаточно малыми, рассуждали эти исследователи, они по-прежнему будут выглядеть как точечные частицы, и, следовательно, не будут противоречить результатам экспериментальных наблюдений. Хотя эта теория была простой и интуитивно привлекательной, вскоре было показано, что описание сильного взаимодействия с помощью струн содержит изъяны. В начале 1970-х гг. специалисты по физике высоких энергий смогли глубже заглянуть в субатомный мир и показали, что ряд предсказаний модели, основанной на использовании струн, находится в прямом противоречии с результатами наблюдений. В то же время параллельно шло развитие квантово-полевой теории — квантовой хромодинамики, — в которой использовалась точечная модель частиц. Успехи этой теории в описании сильного взаимодействия привели к отказу от теории струн.
Большинство специалистов по физике элементарных частиц полагали, что теория струн навсегда отправлена в мусорный ящик, однако ряд исследователей сохранили ей верность. Шварц, например, ощущал, что «математическая структура теории струн столь прекрасна и имеет столько поразительных свойств, что, несомненно, должна указывать на что-то более глубокое».[46] Одна из проблем, с которыми физики сталкивались в теории струн, состояла в том, что она, как казалось, предоставляла слишком богатый выбор, что сбивало с толку. Некоторые конфигурации колеблющихся струн в этой теории имели свойства, которые напоминали свойства глюонов, что давало основание действительно считать ее теорией сильного взаимодействия. Однако помимо этого в ней содержались
Физическое сообщество отреагировало на это предположение весьма сдержанно. В действительности, по воспоминаниям Шварца, «наша работа была проигнорирована всеми».[48] Пути прогресса уже были основательно захламлены многочисленными провалившимися попытками объединить гравитацию и квантовую механику. Теория струн потерпела неудачу в своей первоначальной попытке описать сильное взаимодействие, и многим казалось бессмысленным пытаться использовать ее для достижения еще более великих целей. Последующие, более детальные исследования конца 1970-х и начала 1980-х гг. показали, что между теорией струн и квантовой механикой возникают свои, хотя и меньшие по масштабам, противоречия. Создавалось впечатление, что гравитационная сила вновь смогла устоять перед попыткой встроить ее в описание мироздания на микроскопическом уровне.
Так было до 1984 г. В своей статье, сыгравшей поворотную роль и подытожившей более чем десятилетние интенсивные исследования, которые по большей части были проигнорированы или отвергнуты большинством физиков, Грин и Шварц установили, что незначительное противоречие с квантовой теорией, которым страдала теория струн, может быть разрешено. Более того, они показали, что полученная в результате теория обладает достаточной широтой, чтобы охватить все четыре вида взаимодействий и все виды материи. Весть об этом результате распространилась по всему физическому сообществу: сотни специалистов по физике элементарных частиц прекращали работу над своими проектами, чтобы принять участие в штурме, который казался последней теоретической битвой в многовековом наступлении на глубочайшие основы мироздания.
Я начал работу в аспирантуре Оксфордского университета в октябре 1984 г. Хотя я был восхищен раскрывавшимися передо мной достижениями квантовой теории поля, калибровочной теории и общей теории относительности, среди моих старших коллег-аспирантов было распространено скептическое убеждение, что большая часть открытий физики элементарных частиц уже сделана. Была разработана стандартная модель, и замечательный успех, с которым она предсказывала результаты экспериментов, оставлял мало сомнений в том, что ее полное подтверждение является делом не слишком отдаленного будущего. Выход за ее пределы для включения гравитации и возможного
Период с 1984 по 1986 гг. теперь известен как «первая революция в теории суперструн». В течение этого периода физиками всего мира было написано более тысячи статей по теории струн. Эти работы окончательно продемонстрировали, что многочисленные свойства стандартной модели, открытые в течение десятилетий кропотливых исследований,
Однако на этом пути занимавшиеся теорией струн физики снова и снова натыкались на серьезные препятствия. В теоретической физике часто приходится иметь дело с уравнениями, которые либо слишком сложны для понимания, либо с трудом поддаются решению. Обычно в такой ситуации физики не пасуют и пытаются получить приближенное решение этих уравнений. Положение дел в теории струн намного сложнее. Даже сам
Конец застою положил захватывающий дух доклад, сделанным Эдвардом Виттеном в 1995 г. на конференции по теории струн в университете Южной Калифорнии — доклад, который ошеломил аудиторию, до отказа заполненную ведущими физиками мира. В нем он обнародовал план следующего этапа исследований, положив тем самым начало «второй революции в теории суперструн». Сейчас специалисты по теории струн энергично работают над новыми методами, которые обещают преодолеть встреченные препятствия. Трудности, которые лежат впереди, будут серьезным испытанием для ученых, работающих в этой области, но в результате свет в конце тоннеля, хотя еще и отдаленный, может стать видимым.
В этой и в нескольких последующих главах мы опишем открытия теории струн, явившиеся результатом первой революции и поздних исследований, выполненных до начала второй революции. Время от времени мы будем упоминать достижения, сделанные в ходе второй революции; подробное описание этих новейших достижений будет приведено в главах 12 и 13.
Как мы говорили в начале данной главы, и как показано на рис. 1.1, теория струн утверждает, что если бы мы могли исследовать точечные частицы, существование которых предполагает стандартная модель, с точностью, выходящей далеко за пределы наших современных возможностей, мы бы увидели, что каждая из этих частиц представляет собой крошечную колеблющуюся струну, имеющую форму петли.
По причинам, которые станут ясны в дальнейшем, длина типичной петли, образованной струной, близка к планковской длине, которая примерно в сто миллиардов миллиардов раз (1020) меньше размера атомного ядра. Неудивительно, что современные эксперименты не могут подтвердить струнную природу материи: размеры струн бесконечно малы даже в масштабе субатомных частиц. Для получения прямого подтверждения того, что струна не является точечной частицей, нам потребовался бы ускоритель, способный сталкивать частицы с энергией, в несколько миллионов миллиардов раз превышающей максимальный уровень, достигнутый на сегодняшний день.
Вскоре мы опишем ошеломляющие выводы, следующие из замены точечных частиц струнами, но сначала давайте рассмотрим более фундаментальный вопрос: из чего состоят струны?
Есть два возможных ответа на этот вопрос. Во-первых, струны действительно являются фундаментальными объектами — они представляют собой «атомы»,
Это первый ответ. Второй ответ основывается на том простом факте, что сегодня мы не знаем, верна ли теория струн и является ли она окончательной теорией мироздания. Если теория струн неверна — ну что же, мы можем забыть струны и неуместный вопрос об их структуре. Хотя такая возможность существует, исследования, проводившиеся с середины 1980-х гг., показывают, что ее вероятность крайне мала. Однако история определенно научила нас, что каждый раз, когда мы углубляем наше понимание Вселенной, мы находим все меньшие компоненты микромира, составляющие более тонкий уровень организации материи. Итак, еще одна возможность, в случае если теория струн не окажется окончательной теорией, состоит в том, что струны образуют еще один слой в луковице мироздания, слой, который становится видимым в масштабах планковской длины, но который не является последним слоем. В этом случае струны могут состоять из еще более мелких структур. Специалисты по теории струн осознают такую возможность и ведут теоретические исследования в этом направлении. На сегодняшний день эти исследования привели к некоторым интригующим догадкам о более глубоких уровнях структуры, но они еще не получили окончательного подтверждения. Только время и дальнейшие исследования дадут окончательный ответ на этот вопрос.
За исключением некоторых гипотез, рассматриваемых в главах 12 и 15, мы будем рассматривать струны в том смысле, который следует из первого ответа, т.е. будем считать их наиболее фундаментальными компонентами мироздания.
Помимо неспособности включить в себя гравитационное взаимодействие, стандартная модель обладает еще одним недостатком — она не дает описания устройства объектов, с которыми работает. Почему природа выбрала именно те частицы и взаимодействия, которые были описаны в предыдущих главах и перечислены в табл. 1.1 и 1.2? Почему 19 параметров, которые описывают количественные характеристики этих компонентов, имеют именно те значения, которые имеют? Ученым не удавалось отделаться от чувства, что количество и свойства этих объектов являются совершенно случайными. Скрывается ли за этими, на первый взгляд абсолютно произвольными компонентами, какой-то более глубокий смысл, или физические свойства мироздания являются просто «игрой случая»?
Стандартная модель сама по себе не способна дать объяснения всем этим фактам, поскольку она принимает список частиц и их свойств как полученные экспериментально
На самом деле, если эксперименты покажут, что в микромире существуют какие-то иные частицы или какие-то дополнительные взаимодействия, то в стандартной модели изменения могут быть легко учтены путем замены списка входных параметров. В этом смысле структура стандартной модели обладает слишком большой гибкостью, чтобы дать объяснение свойствам элементарных частиц: она охватывает целый диапазон различных возможностей.
Теория струн имеет совершенно иной характер. Это теоретическое здание единой и жесткой конструкции. Все входные данные, которые ей необходимы, ограничиваются описываемым ниже единственным параметром, который устанавливает шкалу для проведения измерений. Теория струн способна объяснить все свойства микромира. Чтобы понять это, обратимся сперва к более привычным струнам скрипки. Каждая струна может совершать огромное (на самом деле бесконечное) число различных колебаний, известных под названием
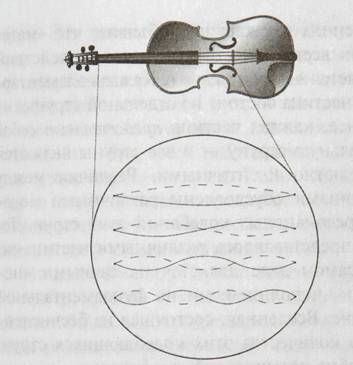 |
Рис. 6.1. У скрипичных струн существуют резонансные моды колебаний, на которых между концами струны укладывается целое число максимумов и минимумов.
Это колебания, у которых расстояние между максимумами и минимумами одинаково, и между закрепленными концами струны укладывается в точности целое число максимумов и минимумов. Человеческое ухо воспринимает резонансные колебания как различные музыкальные ноты. Схожие свойства имеют струны в теории струн. Они могут осуществлять резонансные колебания, в которых вдоль длины струн укладывается в точности целое число равномерно распределенных максимумов и минимумов. Некоторые примеры таких колебаний показаны на рис. 6.2.
Рис. 6.2. Петли теории струн имеют резонансные моды колебаний, похожие на моды резонансных колебаний скрипичных струн. При этом вдоль длины струны укладывается в точности целое число максимумов и минимумов.
Основное утверждение теории струн таково. Точно так же, как различные моды резонансных колебаний скрипичных струн рождают различные музыкальные ноты,
Легче всего понять эту ассоциацию для массы частицы. Энергия конкретной моды колебания струны зависит от ее амплитуды — максимального расстояния между максимумами и минимумами, и от длины волны — расстояния между двумя соседними пиками. Чем больше амплитуда и чем короче длина волны, тем больше энергия. Это совпадает с нашими интуитивными представлениями — более интенсивные колебания несут больше энергии, менее интенсивные — меньше. Пара примеров показана на рис. 6.3.
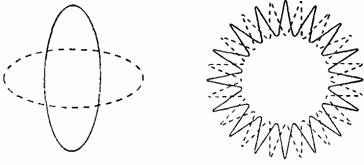 |
Рис. 6.3. Более интенсивные колебания несут большее количество энергии, менее интенсивные — меньшее.
Такая картина, опять же, привычна для нас: если коснуться струны скрипки сильнее, звук будет более сильным, слабое прикосновение даст более нежный звук. Согласно специальной теории относительности энергия и масса представляют собой две стороны одной медали: чем больше энергия, тем больше масса и наоборот. Таким образом, в соответствии с теорией струн,
Поскольку масса частицы определяет ее гравитационные характеристики, существует прямая связь между модой колебания струны и откликом частицы на действие гравитационной силы. Используя несколько более абстрактные рассуждения, физики установили, что существует аналогичное соответствие между иными характеристиками колебания струны и реакцией на другие взаимодействия. Например, электрический заряд, константы слабого и сильного взаимодействия, которые несет частица, в точности определяются типом ее колебания. Более того, тот же самый принцип справедлив и для самих частиц, переносящих взаимодействия. Фотоны, калибровочные бозоны слабого взаимодействия и глюоны представляют собой всего лишь иные моды колебаний струн. Что особенно важно, характеристики одной из мод колебаний струн в точности совпадают с характеристиками гравитона, гарантируя, что гравитация является неотъемлемой частью теории струн.[51]
Таким образом, согласно теории струн наблюдаемые характеристики всех элементарных частиц определяются конкретной модой резонансного колебания внутренних струн. Этот взгляд радикально отличается от точки зрения, которой придерживались физики до открытия теории струн, когда считалось, что различия между фундаментальными частицами обусловлены тем, что они «отрезаны от разных кусков ткани». Хотя частицы считались элементарными, предполагалось, что они состоят из различного «материала». Так, например, «материал» электрона имел отрицательный электрический заряд, а «материал» нейтрино был электрически нейтральными. Теория струн радикально изменила эту картину, объявив, что «материал» всего вещества и всех взаимодействий является
Этот краткий обзор показал, каким образом теория струн дает поистине поразительную объединяющую систему. Каждая частица вещества и каждая частица, переносящая взаимодействие, состоит из струны, мода колебания которой дает «дактилоскопический отпечаток» этой частицы. Поскольку каждое физическое событие, процесс или явление на своем наиболее элементарном уровне может быть описано на языке взаимодействия между этими элементарными компонентами материи, теория струн обещает предоставить в наше распоряжение единое, всеобъемлющее, унифицированное описание физического мира — универсальную теорию мироздания.
Хотя теория струн покончила с предшествующей концепцией элементарных частиц, лишенных внутренней структуры, расставание со старым языком происходит тяжело, особенно когда он дает точное описание действительности вплоть до наименьших доступных масштабов расстояний. Поэтому, следуя сложившимся традициям, мы будем продолжать говорить об «элементарных частицах», но при этом всегда будем помнить, что в действительности это «то, что выглядит элементарной частицей, но на самом деле представляет собой крошечную колеблющуюся струну». В предшествующем разделе мы предположили, что массы и константы взаимодействия таких элементарных частиц связаны с модами колебаний соответствующих струн. Это приводит нас к следующему выводу: если бы мы смогли точно определить все допустимые резонансные моды колебаний фундаментальных струн, — так сказать, «ноты», которые они могут исполнять, мы смогли бы объяснить наблюдаемые свойства элементарных частиц. Таким образом, теория струн впервые предлагает систему, позволяющую
На данной стадии нужно «взять» струну и «притронуться» к ней всеми возможными способами, чтобы определить возможные моды резонансных колебаний. Если теория струн права, возможные резонансные моды точно воспроизведут наблюдаемые свойства перечисленных в табл. 1.1 и 1.2 частиц вещества и частиц, передающих взаимодействия. Конечно, струны слишком малы, чтобы можно было осуществить такой эксперимент в буквальном смысле слова. Вместо этого мы будем «притрагиваться» к струнам
В следующих главах мы более подробно обсудим имеющиеся проблемы, однако полезно сначала ознакомиться с ними в самых общих чертах. Окружающие нас струны могут иметь самое разное натяжение. Например, шнурки на ботинках обычно натянуты намного слабее, чем струны на скрипке. И те и другие, в свою очередь, имеют гораздо меньшее натяжение, чем струны рояля. Единственным параметром, который требуется для калибровки теории струн, является их натяжение. Как определить это натяжение? Если бы мы могли коснуться фундаментальной струны, мы узнали бы ее жесткость и могли бы определить ее натяжение тем же способом, который используется для других, более привычных струн. Но поскольку фундаментальные струны так малы, мы не можем использовать этот подход, и возникает необходимость в разработке косвенного метода. В 1974 г., когда Шерк и Шварц предположили, что одна из мод колебания струн представляет собой гравитон, они смогли использовать такой косвенный метод и определить натяжение, с которыми оперирует теория струн. Их расчеты показали, что интенсивность взаимодействия, передаваемого колебанием струны, соответствующем гравитону, обратно пропорциональна натяжению струны. А поскольку гравитон передает гравитационное взаимодействие, которое является очень слабым, полученное ими значение натяжения оказалось колоссальным: тысяча миллиардов миллиардов миллиардов миллиардов (1039) тонн, так называемое
Во-первых, в то время, как струны рояля закреплены, что гарантирует постоянство их длины, для фундаментальных струн подобного закрепления, ограничивающего их размер, нет. Вместо этого чудовищное натяжение струн заставляет петли, которые рассматриваются в теории струн, сжиматься до микроскопических размеров. Детальные расчеты показывают, что под действием планковского натяжения типичная струна сжимается до планковской длины, т.е. до 10–33 см, как отмечалось выше.[52]
Во-вторых, вследствие такого огромного натяжения типичная энергия колеблющейся петли в теории струн становится чрезвычайно большой. Чтобы понять это, вспомним, что чем больше натяжение струны, тем труднее заставить ее колебаться. Например, заставить колебаться струну скрипки гораздо легче, чем струну рояля. Поэтому две струны, колеблющиеся совершенно одинаковым образом, но натянутые по-разному, будут иметь различную энергию. Струна с большим натяжением будет иметь большую энергию, чем струна с низким натяжением, поскольку для того, чтобы привести ее в движение, потребуется большее количество энергии.
Это говорит о том, что энергия колеблющейся струны зависит от двух вещей: от точного вида колебаний (более интенсивные колебания соответствуют более высокой энергии) и от натяжения струны (более сильное натяжение, опять же, соответствует более высокой энергии). На первый взгляд это описание может привести вас к мысли, что при переходе к более слабым колебаниям, с меньшей амплитудой и с меньшим числом максимумов и минимумов, струна будет обладать все меньшей энергией. Однако, как будет показано в главе 4 (в другом контексте), квантовая механика утверждает, что это рассуждение неверно. Согласно квантовой механике колебания струн, подобно всем другим колебаниям и волноподобным возмущениям, могут иметь только дискретные значения энергии. Грубо говоря, подобно компаньонам из ангара, у которых доверенные им деньги равны произведению
Ключевым моментом здесь является следующее. Поскольку минимальный энергетический номинал пропорционален огромному натяжению струны, минимальная фундаментальная энергия также будет огромна по сравнению с обычными масштабами физики элементарных частиц. Она будет кратна величине, известной под названием
Здесь возникает важный вопрос, имеющий прямое отношение к задаче воспроизведения характеристик частиц в табл. 1.1 и 1.2. Если «естественная» энергетическая шкала теории струн примерно в десять миллиардов миллиардов раз превышает значения энергии и массы протона, как она может использоваться для намного более легких частиц — электронов, кварков, протонов и т. п., — образующих окружающий нас мир?
Ответ снова приходит из квантовой механики. Соотношение неопределенностей гарантирует, что не существует состояния абсолютного покоя. Все объекты испытывают квантовые флуктуации, поскольку в противном случае мы могли бы, в нарушение соотношения Гейзенберга, с абсолютной точностью узнать их местоположение и скорость. Это справедливо и для петель теории струн: независимо от того, насколько спокойной выглядит струна, она всегда в той или иной мере испытывает действие квантовых осцилляции. Замечательный факт, впервые установленный в 1970-х гг., состоит в том, что квантовые осцилляции и обычные колебания струны, которые обсуждались выше и были показаны на рис. 6.2 и 6.3, с энергетической точки зрения взаимно
Из этого следует, что сравнительно легкие фундаментальные частицы табл. 1.1 и 1.2 образуются, в некотором смысле, из тумана, расстилающегося над ревущим океаном высокоэнергетических струн. Даже такая тяжелая частица, как
Это ведет нас к третьему следствию, имеющему огромное значение в теории струн. Существует бесконечное число мод колебаний струны. Для примера на рис. 6.2 мы показали начало бесконечной последовательности вариантов, характеризующих вероятности колебаний с увеличивающимся числом максимумов и минимумов. Не означает ли это существование бесконечной последовательности элементарных частиц, что находилось бы в явном противоречии с современной ситуацией в экспериментальных исследованиях, показанной на табл. 1.1 и 1.2?
Ответом является «да». Если теория струн верна, каждой из бесконечного множества резонансных мод колебаний струн должна соответствовать элементарная частица. Здесь, однако, есть один важный момент. Высокое натяжение струн гарантирует, что за редким исключением эти моды колебаний соответствуют чрезвычайно тяжелым частицам (исключение составляют колебания с минимальной энергией, которые отличаются почти полным сокращением массы ввиду квантовых флуктуации). Слово «тяжелый» здесь опять же означает «во много раз тяжелее планковской массы». Поскольку самые мощные из существующих ускорителей способны достичь энергий порядка тысячи масс протона, что составляет менее одной миллионной от одной миллиардной планковской энергии, возможность лабораторного изучения этих новых частиц, предсказываемых теорией струн, появится еще нескоро.
Существуют, однако, другие, менее прямые способы поиска таких частиц. Например, энергии при возникновении Вселенной были достаточно высокими, чтобы такие частицы появлялись в изобилии. Вообще говоря, вряд ли можно ожидать, что эти частицы дожили до наших дней, поскольку сверхтяжелые частицы обычно нестабильны и высвобождают свои огромные массы путем последовательного распада на все более легкие частицы, превращаясь, в конце концов, в обычные, относительно легкие частицы окружающего нас мира. Однако существует вероятность того, что такое сверхтяжелое состояние колебаний струны, являющееся реликтом эпохи Большого взрыва, могло дожить до наших дней. Открытие таких частиц, которое будет обсуждаться подробнее в главе 9, стало бы эпохальным событием.
Единая схема, которую дает теория струн, очень привлекательна. Но истинную неотразимость придает ей возможность избавиться от вражды между гравитационным взаимодействием и квантовой механикой. Вспомним, что проблема при объединении общей теории относительности и квантовой механики возникает, когда основное понятие первой из них — плавно искривленная геометрическая структура пространства и времени — сталкивается с главной особенностью второй, что все во Вселенной, включая структуру пространства и времени, испытывает квантовые флуктуации, интенсивность которых растет при уменьшении масштаба исследований. На субпланковском масштабе расстояний квантовые флуктуации становятся столь сильными, что приводят к разрушению понятия гладкого искривленного геометрического пространства, и это означает нарушение принципов общей теории относительности.
Теория струн смягчает неистовые квантовые флуктуации путем «размазывания» микроскопических характеристик пространства. На вопрос о том, что это значит в действительности и как это разрешает противоречие, есть два ответа: грубый и более точный. Мы поочередно рассмотрим каждый из них.
Хотя это звучит довольно наивно, один из способов, которым мы можем изучить структуру какого-либо объекта, состоит в том, чтобы бросать в него другие предметы и наблюдать за тем, как они отражаются от него. В качестве примера укажем, что мы способны видеть предметы потому, что наши глаза собирают, а наш мозг расшифровывает информацию, которую несут фотоны, отражающиеся от объектов, на которые мы смотрим. На этом же принципе основаны ускорители частиц: в них частицы материи, например, электроны и протоны, сталкиваются между собой и с другими объектами; затем специальные детекторы анализируют разлетающиеся осколки для получения информации, позволяющей определить структуру объектов, участвующих в столкновениях.
Общее правило при таких исследованиях состоит в том, что
Лучшее, что удалось изобразить Слиму, показано на рис. 6.4а
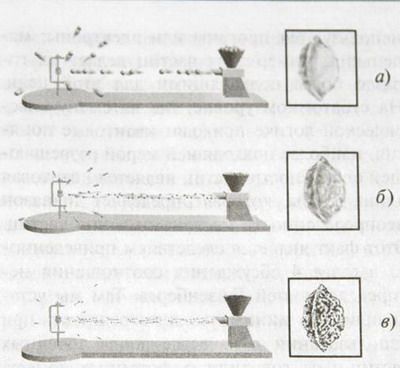 |
Рис. 6.4. Персиковая косточка закреплена в тисках. Для создания ее изображения используются только наблюдения за тем, как отскакивают предметы — «зонды», — брошенные в нее. Используя зонды все меньшего размера — шарики (а), пятимиллиметровые пульки (б), полумиллиметровые пульки (в), можно получать все более детальное изображение.
Урок, который можно извлечь из этого маленького состязания, ясен: размер частиц-зондов не может существенно превышать размер изучаемых физических особенностей; в противном случае разрешающая способность исследования окажется недостаточной для изучения интересующих нас структур.
Те же самые выводы относятся, конечно, и к случаю, когда мы захотим провести более глубокое исследование персиковой косточки, чтобы определить ее структуру на атомном и субатомном уровне. Полумиллиметровые пульки не дадут никакой полезной информации по этому вопросу; они явно слишком велики, чтобы исследовать структуру на атомном уровне. Именно по этой причине в ускорителях в качестве зондов используются протоны или электроны: маленький размер этих частиц делает их гораздо более подходящими для этой цели. На субатомном уровне, где на смену классической логике приходят квантовые понятия, наиболее подходящей мерой разрешающей способности частиц является квантовая длина волны, которая определяет диапазон неопределенности местонахождения частиц. Этот факт является следствием приведенного в главе 4 обсуждения соотношения неопределенностей Гейзенберга. Там мы установили, что минимальная погрешность при использовании в качестве зонда точечных частиц (мы говорили о фотонных зондах, но сказанное применимо и ко всем другим частицам) примерно равна квантовой длине волны частицы, используемой в качестве зонда. Грубо говоря, разрешающая способность точечной частицы размазывается в результате действия квантовых флуктуации подобно тому, как точность скальпеля хирурга уменьшается, когда его руки дрожат. Вспомним, однако, что в главе 4 мы также отметили один важный факт, состоящий в том, что квантовая длина волны частицы обратно пропорциональна моменту количества движения, который, грубо говоря, определяется ее энергией. Таким образом, увеличивая энергию точечной частицы, можно делать ее квантовую длину волны все меньше и меньше, квантовое размазывание будет все более уменьшаться и, следовательно, мы сможем использовать эту частицу для изучения все более тонких структур. Интуитивно понятно, что частицы высокой энергии имеют большую проникающую способность и могут использоваться для изучения более мелких деталей строения.
В этом смысле становится очевидным различие между точечными частицами и нитями струн. Как в примере с пластиковыми пульками для изучения структуры поверхности персиковой косточки, присущая струне пространственная протяженность не позволяет использовать ее для исследования объектов, размер которых существенно меньше размера струны, в нашем случае — объектов, характерные размеры которых меньше планковской длины. Если перейти к более точным формулировкам, в 1988 г. Дэвид Гросс, работавший в то время в Принстонском университете, и его студент Пол Менде показали, что если учитывать квантовую механику, то непрерывное увеличение энергии струны
Но ведь конфликт между общей теорией относительности и квантовой механикой возникает благодаря свойствам структуры пространства, проявляющимся в субпланковском масштабе расстояний.
Существенное различие между аналогией с гранитом и нашей реальной проблемой структуры пространства состоит в том, что существуют способы обнаружить микроскопическую дискретность поверхности гранита. Для этого могут использоваться более точные зонды, чем наши пальцы. Электронный микроскоп способен обнаружить поверхностные структуры, размер которых составляет менее одной миллионной доли сантиметра; этого достаточно, чтобы увидеть многочисленные неровности на поверхности. В противоположность этому, в теории струн нет способа обнаружить «неровности» в структуре пространства на субпланковском уровне. Во Вселенной, управляемой законами теории струн, уже не является истинной обычная точка зрения, согласно которой мы можем без ограничения делить объекты на все более и более мелкие части. Предел
Обсуждение, приведенное выше, может оставить у вас чувство неудовлетворенности. Вместо того чтобы показать, что теория струн укрощает субпланковские флуктуации структуры пространства, мы, похоже, использовали ненулевой размер струн для того, чтобы обойти всю проблему стороной. Решили ли мы вообще хоть что-нибудь? Решили. Следующие два соображения позволят нам лучше понять это.
Прежде всего вывод, который можно сделать из предыдущего обсуждения, состоит в том, что предполагаемые флуктуации структуры пространства в масштабе субпланковских расстояний связаны исключительно с формулировкой общей теории относительности и квантовой механики в рамках модели, основанной на точечных частицах. Это означает, что центральное противоречие современной теоретической физики в определенном смысле является проблемой, которую породили мы сами. Поскольку мы ранее предположили, что все частицы вещества и все частицы, передающие взаимодействие, должны быть точечными объектами, практически не имеющими пространственной протяженности, мы были обязаны рассматривать свойства Вселенной на произвольно малых масштабах. И на самых малых расстояниях мы столкнулись с проблемой, выглядящей неразрешимой. Теория струн утверждает, что мы столкнулись с этой проблемой только потому, что не поняли истинных правил игры: новые правила гласят, что существует предел тому, насколько глубоко можно исследовать Вселенную, — предел, определяющий, до какого уровня наше обычное понятие расстояния может применяться к ультрамикроскопической структуре мироздания. Становится понятно, что фатальные флуктуации структуры пространства возникают в наших теориях из-за неосведомленности об этих пределах: модель с точечными частицами далеко выходит за рамки физической реальности.
Видя кажущуюся простоту этого решения, позволяющего разрешить конфликт, возникающий между общей теорией относительности и квантовой механикой, вы можете удивиться, почему прошло столько времени, пока ученые не осознали, что точечная модель частиц всего лишь идеализация, и что в реальном мире элементарные частицы имеют некоторые конечные размеры. Это второй момент, на который мы хотели бы обратить внимание. Уже давно некоторые из величайших умов теоретической физики, такие как Паули, Гейзенберг, Дирак и Фейнман,
Грубый ответ ухватывает сущность того, почему теория струн смогла добиться успеха там, где предшествующие теории, основанные на точечной модели частиц, потерпели неудачу. Поэтому без ущерба для понимания дальнейшего можно сразу перейти к следующему разделу. Однако, рассмотрев в главе 2 основные идеи специальной теории относительности, мы получили в свое распоряжение средства, позволяющие более точно описать, как теория струн борется с разрушительными квантовыми флуктуациями.
В более точном ответе мы будем использовать те же основные идеи, которые содержались в приближенном ответе, но выразим их непосредственно на языке струн. Мы увидим, как конечность размера струн «размазывает» информацию, которую можно было бы получить при зондировании с использованием точечных частиц, и тем самым, к нашему счастью, снимает проблему поведения пространства на ультрамикроскопических расстояниях, ответственную за центральную дилемму современной физики.
Сначала рассмотрим, как происходило бы взаимодействие между точечными частицами, если бы они действительно существовали, и, соответственно, как можно было бы использовать их в качестве физических зондов. Наиболее важным является показанный на рис. 6.5 случай взаимодействия между частицами, движущимися по пересекающимся путям, приводящим к столкновению. Если бы эти частицы были бильярдными шарами, они могли бы столкнуться, после чего каждая из них начала бы двигаться по новой траектории. Квантовая теория поля с точечными частицами показывает, что то же самое происходит при столкновении элементарных частиц — они отскакивают друг от друга и продолжают свой путь по новым траекториям — однако детали этого процесса отличаются.
 |
Рис. 6.5. Две частицы взаимодействуют: они «сталкиваются между собой», и это приводит к изменению траектории каждой из них.
Для большей определенности и простоты представим себе, что одна из двух частиц является электроном, а другая — ее античастицей, позитроном. При столкновении частицы и античастицы они аннигилируют с выделением энергии в чистом виде, приводящим к образованию, например, фотона.[54] Чтобы отличать выходящую траекторию фотона от входящих траекторий электрона и позитрона, мы будем, следуя принятому в физике соглашению, изображать ее волнистой линией. Обычно фотон проходит небольшое расстояние, после чего высвобождает энергию, полученную от первоначальной электрон-позитронной пары, путем образования другой электрон-позитронной пары, показанной в правой части рис. 6.6.
 |
Рис. 6.6. В квантовой теории поля частица и ее античастица могут мгновенно аннигилировать с образованием фотона. Затем этот фотон порождает другую частицу и античастицу, которые движутся по расходящимся траекториям.
Эти две частицы испытывают электромагнитное взаимодействие и, в конце концов, разлетаются по расходящимся траекториям. Такая последовательность событий имеет определенное сходство с описанием бильярдных шаров.
Нас интересуют детали взаимодействия, в частности, точка, где начальные электрон и протон аннигилируют с образованием фотона. Как станет ясно далее, главным является тот факт, что время и место этого события могут быть установлены однозначно и точно, как показано на рис. 6.6.
Как изменится описание, приведенное выше, если после тщательного исследования объектов, которые мы считали нульмерными точками, они окажутся одномерными струнами? Основной процесс взаимодействия будет тем же самым, но теперь движущиеся по пути к столкновению объекты представляют собой осциллирующие петли, показанные на рис. 6.7. Для определенных колебаний струны ее моды будут как раз соответствовать протону и электрону, движущихся курсом на столкновение, как показано на рис. 6.6. Истинный струнный характер становится очевидным только при исследовании в ультрамикроскопическом масштабе, выходящем далеко за пределы современных экспериментальных возможностей. Как и в случае с точечными частицами, две струны сталкиваются и аннигилируют, превращаясь во вспышку, которая представляет собой фотон и сама по себе является струной, колеблющейся в определенной моде. Таким образом, две исходные струны взаимодействуют между собой, сливаясь и образуя третью струну, как показано на рис. 6.7. Как и в случае точечных частиц, эта струна проходит некоторое расстояние, после чего выделяет энергию, полученную от двух исходных струн, разделяясь на две новые струны, которые продолжают движение. Опять же, со всех точек зрения, кроме той, которая относится к микроскопическим масштабам, это будет выглядеть идентично взаимодействию между точечными частицами на рис. 6.6.
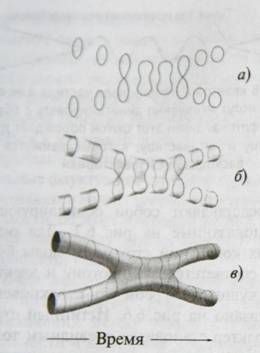 |
Рис. 6.7. а) Две струны, движущиеся курсом на столкновение, могут слиться и образовать третью струну, которая вслед за этим может разделиться на две струны, движущиеся по расходящимся траекториям. б) Тот же процесс, что и на рис. а), но более явно прослеживающий движение струн, в) «Замедленная киносъемка» двух взаимодействующих струн дает мировую поверхность.
Существует, однако, радикальное различие между этими двумя описаниями. Мы подчеркнули, что взаимодействие между точечными частицами происходит в однозначно идентифицируемой точке пространства и времени, в точке, с положением которой согласятся все наблюдатели. Как мы сейчас увидим, для взаимодействия между струнами это
Представим, что мы наблюдаем за взаимодействием двух струн с помощью фотокамеры, затвор которой остается открытым, и вся хронология процесса регистрируется на одном фрагменте пленки.[55] На рис. 6.7в показан результат: его называют
Пример такого разрезания показан на рис. 6.8. В частности, на рис. 6.8а мы показали Джорджа, пристально наблюдающего за двумя сближающимися частицами, а также плоскость, которая вычленяет
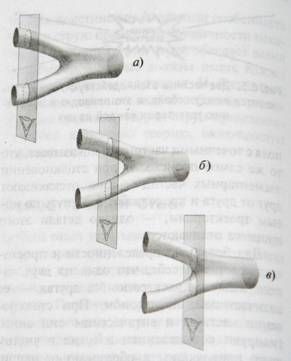 |
Рис. 6.8. Две исходные струны (с точки зрения Джорджа) в три последовательных момента времени. В моменты а) и б) струны сближаются, в момент в), с его точки зрения, они впервые соприкоснулись.
Как часто делалось в предыдущих главах, для наглядности мы отбросили на диаграмме одно пространственное измерение. На самом деле, конечно, существует трехмерный массив событий, которые происходили одновременно для любого наблюдателя.
На рис. 6.8б и 6.8в приведены два последовательных моментальных снимка — два последовательных «среза» мировой поверхности, — показывающих, как Джордж видит две струны, приближающиеся друг к другу. Особую важность имеет отмеченный на рис. 6.8 в момент, когда, с точки зрения Джорджа, две струны войдут в соприкосновение и сольются, образовав третью струну.
А теперь повторим все то же самое для Грейс. Как мы указывали в главе 2, относительное движение Джорджа и Грейс приведет к тому, что они не согласятся по вопросу о том, какие события являются одновременными. С точки зрения Грейс события в пространстве, являющиеся одновременными, лежат в другой плоскости, показанной на рис. 6.9. Иными словами, по мнению Грейс, для того чтобы момент за моментом восстановить процесс взаимодействия, мировая поверхность на рис. 6.7в должна быть «нарезана» на куски под другим углом.
На рис. 6.9б и 6.9в мы снова показали последовательные моменты времени, но теперь уже с точки зрения Грейс, включая момент, когда две начальные струны по ее наблюдениям войдут в соприкосновение и образуют третью струну.
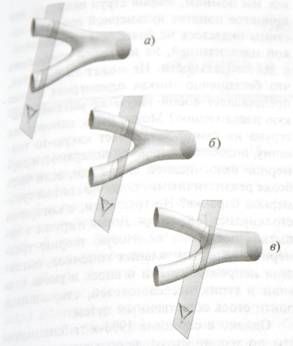 |
Рис. 6.9. Две исходные струны (с точки зрения Грейс) в три последовательных момента времени. В моменты а) и б) струны сближаются, в момент в), с ее точки зрения, они впервые соприкоснулись.
Сравнивая рис. 6.8в и 6.9в (результат показан на рис. 6.10), мы видим, что мнения Джорджа и Грейс разделятся относительно того, где и когда две исходные струны впервые соприкоснулись, т.е. где они взаимодействовали.
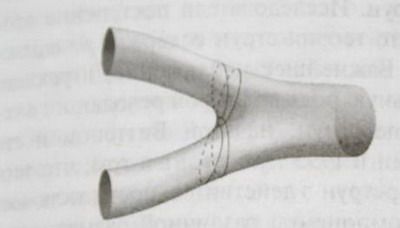 |
Рис. 6.10. Мнения Джорджа и Грейс по вопросу о месте, в котором произошло взаимодействие, разойдутся.
Поскольку струна является протяженным объектом, это означает, что
Если применить те же самые рассуждения к взаимодействию точечных частиц, как показано на рис. 6.11, мы вновь придем к выводам, которые уже получили ранее:
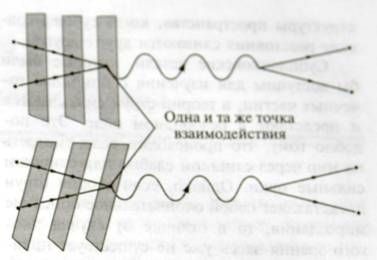 |
Рис. 6.11. Наблюдатели, находящиеся в относительном движении, придут к согласию о месте и времени взаимодействия между двумя частицами.
Все взаимодействие точечных частиц происходит в одной определенной точке. Когда сила, связанная со взаимодействием, представляет собой гравитационную силу, т.е. когда частица, передающая взаимодействие, является гравитоном, а не фотоном, такая упаковка всей энергии взаимодействия в одну точку ведет к катастрофическим результатам, вроде упоминавшихся ранее бесконечных ответов. В противоположность этому струны «размазывают» место, в котором происходит взаимодействие. Поскольку разные наблюдатели регистрируют взаимодействие происходящим в разных точках левой части поверхности на рис. 6.10, это означает, что точка взаимодействия в действительности размазана по всей этой области. Это увеличивает область, в которой происходит взаимодействие, и в случае гравитационной силы такое размазывание существенно смягчает ультрамикроскопические свойства, настолько, что вычисления дают нормальные конечные результаты вместо получавшихся ранее бесконечностей. Это более точная версия того размазывания, о котором шла речь в грубом ответе в предыдущем разделе. Подчеркнем еще раз, что это размазывание приводит к сглаживанию ультрамикроскопических флуктуации структуры пространства, когда субпланковские расстояния сливаются друг с другом.
Субпланковские детали, которые были бы доступны для изучения с помощью точечных частиц, в теории струн смазываются и предстают в безобидном виде. Это подобно тому, что происходит, если смотреть на мир через слишком слабые или слишком сильные очки. Однако, если теория струн представляет собой окончательное описание мироздания, то в отличие от случая плохого зрения здесь уже не существует никаких «корректирующих линз», через которые смогли бы отчетливо проявиться предполагаемые субпланковские флуктуации. Несовместимости общей теории относительности и квантовой механики, проявляющейся только в масштабе субпланковских расстояний, можно избежать во Вселенной, где есть нижний предел для расстояний, которые доступны для исследований или которые существуют в обычном смысле этого слова. Такова Вселенная, описываемая теорией струн: в ней законы макромира и микромира могут быть без ущерба объединены, после того как мы покончили с воображаемой катастрофой, возникающей на ультрамикроскопических расстояниях.
Струны имеют две важных особенности. Во-первых, несмотря на конечность пространственных размеров, они могут быть непротиворечиво описаны в рамках квантовой механики. Во-вторых, среди резонансных мод колебаний имеется мода, свойства которой в точности совпадают со свойствами гравитона: тем самым гарантируется, что гравитационное взаимодействие представляет собой неотъемлемую часть этой теории. Однако, как мы помним, теория струн показала, что принятое понятие нульмерной точечной частицы оказалось не более чем математической идеализацией, не имеющей отношения к действительности. Не может ли быть так, что бесконечно тонкая одномерная струна представляет собой такую же математическую идеализацию? Может быть, одномерная струна на самом деле имеет какую-то толщину, подобно внутренней поверхности двумерной велосипедной шины или, если быть более реалистичными, подобно тонкой трехмерной баранке? Но трудности, с которыми столкнулись Гейзенберг, Дирак и другие в попытках построить квантовую теорию трехмерных фундаментальных комочков, выглядели непреодолимыми и вновь и вновь ставили в тупик исследователей, старавшихся пойти столь естественным путем.
Однако в середине 1990-х гг. специалисты по теории струн, используя косвенные и довольно сложные рассуждения, несколько неожиданно установили, что подобные фундаментальные объекты действительно играют важную и нетривиальную роль в самой теории струн. Исследователи постепенно осознали, что теория струн содержит не только струны. Важнейшее наблюдение, играющее центральную роль во второй революции в теории суперструн, начатой Виттеном и его коллегами в 1995 г., состоит в том, что теория суперструн в действительности включает в себя компоненты различной размерности: элементы, похожие на двумерные фрисби-диски, на трехмерные капли, и даже еще более экзотические конструкции. Эти новейшие достижения будут рассмотрены в главах 12 и 13. А пока будем следовать хронологии открытий и обсудим новые поразительные свойства Вселенной, состоящей не из нульмерных точечных частиц, а из одномерных струн.
| © 2024 Библиотека RealLib.org (support [a t] reallib.org) |