Цифры различныхъ народовъ

Немного есть наукъ, которыя свое начало вели бы съ такихъ древнихъ временъ, какъ ариѳметика. И среди этихъ немногихъ своихъ спутницъ ариѳметика является наукой самой отвлеченной. Но если ужъ теперь, несмотря на то, что цивилизація и общее развитіе значительно проникли въ массу народа, всякое отвлеченное мышленіе все же очитается чѣмъ-то сухимъ и труднымъ, то тѣмъ болѣе во времена давно прошедшія отвлеченное знаніе нуждалось обязательно во внѣшнемъ проявленіи. Цифры и служатъ такимъ проявленіемъ. Онѣ всеобщи и такъ же древни, какъ древни крайніе зачатки ариѳметики. Такъ, цифры у египтянъ мы видимъ за 2200 лѣтъ до Р. Хр. въ папирусѣ Ринда, у халдеевъ за 2300 лѣтъ до Р. X. въ табличкахъ Сенкере и у китайцевъ за 2637 лѣтъ до Р. X. въ «Кіу-чангѣ», составленномъ ученымъ авторомъ Тзинъ-кіу-чау. Много есть разныхъ сортовъ цифръ; они отличаются другъ отъ друга и происхожденіемъ, и начертаніемъ, въ зависимости отъ того, когда они получили начало и у какого именно народа.

Навѣрное, читатель, вамъ приходилось не разъ замѣчать, что малые ребята съ особенной охотою рисуютъ дома, людей, животныхъ, т.-е. все то, что прямо предъ глазами, и лишь потомъ, впослѣдствіи они берутся за условные рисунки, т.-е. значки, планы и чертежи. Такъ точно и народы древности предпочитали имѣть цифры въ видѣ рисунковъ тѣхъ предметовъ, которые у нихъ передъ глазами. Особенно замѣтна эта оклонность у древнихъ египтянъ, хотя и у другихъ народовъ мы можемъ указать подобные слѣды. Это письмо носитъ названіе гіероглифичеекаго; напр., чертежъ шеста или кола обозначалъ собою единицу; десятокъ означался фигурою 2-хъ соединенныхъ рукъ, такъ какъ на 2 рукахъ бываетъ 10 пальцевъ; символомъ сотни считался свернутый пальмовый листъ, такъ какъ съ его развитіемъ выходитъ изъ него много листовъ, можетъ быть до 100; тысяча рисовалась въ видѣ цвѣтка лотоса, который знаменовалъ собой обиліе; цифрой, которая обозначала 10000, было изображеніе лягушки, такъ какъ лягушки при разливахъ Нила являлись въ неисчислимомъ количеетвѣ, многими тысячами. Картиной милліона была фигура изумленнаго человѣка.

Такими гіероглифами пользовался Египетъ для выраженія всѣхъ чиселъ. Подобная система была и у халдеевъ. У римлянъ цифра V напоминаетъ своей формой кисть руки. Но, очевидно, писать при помощи рисунковъ крайне медлительно и неудобно, въ особенности же потому, что каждый изъ рисунковъ необходимо было повторять по многу разъ. Такъ, чтобы выразить число хоть 30270, египтянинъ 3 раза рисовалъ лягушку, 2 раза листъ и 7 разъ сложенныя руки. Гіероглифы надо было упростить, снабдить ихъ легкой формой и примѣнимостыо къ письму. Виѣсто фигуръ стали чертить лишь облики, нѣчто въ родѣ условныхъ знаковъ. Такъ получились цифры. Вромѣ того, писать одинъ и тотъ же знакъ по многу разъ невыгодно и долго, поэтому египтяне придумали для чиселъ 2, 3, 4, 9 свои особые значки, которые давали имъ возиожность избѣжать длиннаго и утомительнаго повторенія цифры 1. Что же касается 5, 6, 7, 8, то эти цифры у египтянъ были составлены изъ 2, 3, 4.

Слѣды письма гіероглифами, какъ сказано уже выше, мы видимъ у халдеевъ. Но и они оставили эту систему и выработали вмѣсто нея новую, очень послѣдовательную и простую, такъ называемое клинообразное письмо. Чтобъ обозначить единицу, халдеи рисовали вертикальную черту съ заостреннымъ нижнимъ краемъ и толстымъ расщепленнымъ верхнимъ. Десятокъ означался такою же чертой, но только въ положеніи горизонтальномъ и съ острымъ краемъ, обращеннымъ влѣво. Для выраженія нѣсколькихъ единицъ халдеи повторяли столько разъ знакъ единицы, еколько ихъ содержалось въ данномъ чиелѣ. Такъ, напр., чтобы выразить 7 единицъ, они писали 7 разъ знакъ единицы. Такимъ же образомъ они писали и десятки. Сотню оии обозначали помощью 2 чертъ, горизонтальной вмѣстѣ съ вертикальной. Для чиселъ, состоящихъ изъ полныхъ сотенъ порядокъ видоизмѣнялся: именно, халдеи брали знакъ сотни и при немъ писали столько разъ единицу, сколько сотенъ въ заданномъ числѣ. Для тысячи халдеи не имѣли особенной цифры, и они обозначали тысячу, какъ десять согенъ. И такъ, халдейская система цифръ, равно какъ и египетская, основаны на непосредственной наглядности, и отъ нея уже онѣ переходятъ къ условнымъ знакамъ.

Еще такого же происхожденія мы видимъ цифры у китайцевъ. Въ первоначальной своей формѣ онѣ напоминаютъ картины тѣхъ шнуровъ и косточекъ, которые употреблялись при наглядномъ счетѣ. Впослѣдствіи цифры китайцевъ сильно измѣнились и приняли нѣсколько видовъ. У нихъ есть разныя цифры: древне — китайскія, торговыя, научныя и для правительственныхъ актовъ. Цифры древне-китайскія очень фигурны и замысловаты и весьма возможно, что онѣ явились измѣненіемъ начальныхъ гіероглифовъ; онѣ писались на листкахъ не въ строчку, а вертикальнымъ столбикомъ, располагаясь сверху внизъ. Наоборотъ, цифры торговыя писались горизонтальными строками и шли слѣва направо; при этомъ числа разлагались на разряды, такъ что разрядъ писался за разрядомъ. Чтобы прочесть число, китайцы прямо говорили тѣ слова, какія соотвѣтствуютъ написанному ряду цифръ; согласно ихъ произношенію, тридцать = три десять, тринадцать = десять три, девяносто = девять десять.

Итакъ, у египтянъ, халдеевъ и китайцевъ мы видимъ дифры древнѣйшаго происхожденія, которыя напоминаютъ собою гіероглифы, или картины тѣхъ предметовъ, которые стоятъ въ связи съ даннымъ числомъ. Другимъ основнымъ корнемъ, давшимъ начало цифрамъ, являются числительныя имена. Это уже цифры болѣе позднѣйшія, такъ какъ для ихъ изображенія необходимо было развиться алфавиту, грамотности, потребности въ письмѣ и достаточному искусству письменнаго изложенія. У нѣкоторыхъ народовъ, какъ, напр., у финикіянъ, нерѣдко выписывались числителъныя имена сполна, черезъ посредство буквъ и словъ: финикіяне прямо записывали числа, согласно ихъ произношенію, словами, а не пользовались особыми значками — цифрами. Иногда такой же способъ примѣняли и греки, но особенно его любили арабы. Существуетъ цѣлый учебникъ по ариѳметикѣ араба Алькархи (въ 11 ст. по Р. X.), гдѣ нѣтъ ни одной цифры, и всѣ вычисленія, даже довольно сложныя, выполнены словесно.

Но очевидно, что подобное выписываніе числительныхъ именъ крайне неудобно и утомительно. Въ силу этого, числительныя имена стали подвергаться сокращенію. и цифрами стали считаться начальныя буквы числительныхъ именъ. Примѣровъ этому мы видимъ много у грековъ и у римлянъ, у индусовъ и у арабовъ (въ ихъ позднѣйшихъ цифрахъ). Греческія слова «пять» (πέντε), десять (δέχα), тысяча (χίλιοι), десять тысячъ (μύριοι) начинались съ буквъ π, δ, χ, μ, поэтому именно такія буквы являлись у грековъ знаками для чиселъ 5, 10, 1000, 10000, такъ что, согласно первоначальному греческому обозначенію, число пять имѣло цифру π, десять δ, тысяча χ, и, наконецъ, десять тысячъ μ. Подобный счетъ описанъ византійскимъ грамматистомъ Геродіаномъ, и этотъ сортъ греческихъ цифръ называется геродіановыми цифрами. Подобной же системой воспользовались и арабы, когда они, наконецъ, поняли, что полностью писать числительныя имена довольно затруднительно, они тоже стали писать только начальныя буквы числительныхъ именъ.

И наконецъ, послѣдней стадіей развитія, хотя и близкой къ нашимъ временамъ, но вовсе неудобной, и потому оставленной, надо признать такой порядокъ, когда замѣной цифръ служили буквы въ послѣдовательности алфавита. Такъ напр., греческій алфавитъ содержитъ по порядку буквы: α, β, γ, δ, ε, въ виду этого и числа обозначались: единица — α, два—β, три—γ, четыре — δ, пять—ε. Греки придумали обозначать такимъ образомъ приблизительно со временъ Рождества Христова, а до этого они прибѣгали къ геродіановымъ цифрамъ. Вслѣдствіе этого буква δ стала обозначать уже не десять, какъ начальная буква греческаго слова «δέχα», что значитъ десять, но она стала выражать четыре, какъ 4-я буква алфавита. Какое же удобство въ этихъ позднѣйшихъ цифрахъ сравнителыш съ тѣми, которыя указалъ Геродіанъ? Ариѳметически нѣтъ совершенно никакого, и пользы отъ замѣны однихъ значковъ другими не представляется никакой; виной такой замѣны явились, вѣроятно, переписчики, которымъ слишкомъ трудно было помнить буквы вразбросъ и въ безпорядкѣ: они и предпочли расположить ихъ въ порядкѣ. Подобную же систему мы видимъ у славянъ и у евреевъ. Несомнѣнно, она заимствована отъ грековъ.

Повторимъ вкратцѣ еще разъ, что цифры всѣхъ народовъ и временъ распредѣляются на три разряда: 1) цифры, получившія начало отъ гіероглифовъ и обратившіяся въ условные знаки; 2) цифры, образовавшіяся изъ буквъ алфавита и представляющія собой начальныя буквы числительныхъ именъ, и 3) цифры въ порядкѣ буквъ алфавита. Вторая категорія цифръ тоже измѣнилась, подобно первой, въ нѣкоторыхъ случаяхъ до неузнаваемости, такъ что изъ буквъ образовались условные знаки.

Теперь мы сообщимъ нѣкоторыя подробности о цифрахъ отдѣльныхъ народовъ[3]

Египтяне. Они были образованнымъ народомъ уже за 4000 лѣтъ до Р. X. Періодическіе разливы Нила рано побудили ихъ заниматься землемѣріемъ и ариѳметикой, такъ какъ каждую весну приходилось имъ снова размѣрять, расчислять и дѣлить поля, затянутыя иломъ

могучей рѣки. Въ 1872 году въ тайникахъ одной изъ многочисленныхъ египетскихъ цирамидъ нашли свертокъ пергамента, такъ наз. папирусъ «Риндъ», въ которомъ разобрали рукопись ариѳиетическаго содержанія. Авторъ ея нѣкто египтянинъ Амесъ, жившій во времена фараона Аменемы (2221–2179 г. до Р. X.). Изъ рукописи можно усмотрѣть, что автору доступны были довольно сложныя задачи замысловатаго характера не только въ цѣлыхъ числахъ, но и съ дробями.

У египтянъ было три системы письма: а) гіероглифическая, о которой упомянуто выше, в) гіератическая, или письмо жрецовъ, и с) простонародная. Письмо гіератическое является ничѣмъ инымъ, какъ упрощеніемъ гіероглифовъ, и въ этомъ смыслѣ его можно считать нормальнымъ переходомъ къ цифрамъ. Пользуясь знаками единицы, десятка, сотни, тысячи, египтяне ихъ повторяли столько разъ, сколько хотѣли обозначить единицъ, десятковъ и т. д.; но выше 1000 въ гіератическомъ письмѣ они вводили умноженіе: такъ, чтобы обозначить 10000, они писали рядомъ 10 и 1000. Письмо простонародное преподавалось въ школахъ и примѣнялось въ обиходной жизни, въ торговлѣ, письмахъ, въ гражданскихъ документахъ. Оно имѣло, въ свою очередь, не мало разныхъ видовъ; одинъ изъ нихъ нами показанъ въ приложеніи 3-мъ. Когда египтяне имѣли дѣло съ большими числами, то высшіе разряды они писали слѣва, а низшіе направо, т.-е. точь въ точь, какъ мы.

Финикіяне. Они были моряками и купцами древняго міра. Имъ приписывается изобрѣтеніе алфавита и успѣшное развитіе ариѳметическихъ знаній. Алфавитъ финикіянъ состоялъ изъ 22 буквъ, похожихъ на египетскіе гіероглифы. Служили-ль эти буквы также и для обозначенія чиселъ, на это нѣтъ никакихъ указаній. Напротивъ того, несомнѣнно, что финикіяне или писали сполна слова, выражающія числа, или же пользовались особыми, спеціальными цифрами. Изъ этихъ цифръ и составлялись обозначенія чиселъ, при чемъ рядомъ стоящія цифры иногда являлись множителями другъ друга, иногда же онѣ подлежали сложенію. Числа отъ 1 до 9 обозначались соотвѣтственнымъ количествомъ вертикальныхъ черточекъ. Горизонтальная черта или уголъ, обращенный отверстіемъ внизъ, обозначали число 10. Налѣво (не не направо, какъ написали бы мы) отъ этого знака раcполагали 1, 2, 3 и т. д. вертикальныхъ черты, для обозначенія чиселъ отъ 11 до 19. Такъ, напр. «||||—» обозначало четырнадцать. Чтобы обозначить два десятка, финикіяне писали 2 параллельныхъ черты, которыя лежали горизонтально. Для 100 былъ тоже особый знакъ, именно Ilt;I.

Изъ Тира и Сидона, древнихъ финикійскихъ городовъ, расположенныхъ на берегу Средизеинаго моря, центровъ тогдашней торговли, процвѣтавшихъ съ XIV до VIII вѣка до Р. X., распространилось счетное искусство по финикійскимъ колоніямъ, которыя были разсѣяны по берегу Сѣверной Африки и южнымъ полуостровамъ Европы.

Халдеи, смѣшавшіеся съ вавилонянами и подчинившіе ихъ себѣ, жили на южномъ теченіи рѣкъ Тигра и Евфрата. Это сосѣди и счастливые противники іудеевъ ветхаго завѣта. Культура ихъ принадлежитъ къ древнѣйшимъ: она началась болѣе чѣмъ за 3000 лѣтъ до Р. X., и пришла въ упадокъ за 500 лѣтъ до Р. X. Халдеи употребляли для письма нѣчто въ родѣ грифелей, съ расщепленными концами, поэтому-то мы и видимъ у нихъ такъ назыв. клинообразное письмо. Цифры халдеевъ приведены выше и представлены подробно въ приложеніи 4-мъ, въ концѣ книги. Ихъ можно хорошо установить, благодаря счастливой находкѣ, которую удалось сдѣлать въ развалинахъ древняго знаменитаго города Ниневіи. Тамъ подъ грудой мусора, пыли и пепла археологи открыли цѣлую сохранившуюся залу, по нашему сказать, библіотеку, устроенную по приказанію царя Сарданапала за 7 столѣтій до Р. X. Это была публичная библіотека. Вотъ еще когда и вотъ еще въ какихъ странахъ открывались публичныя библіотеки! Но книгъ въ ней не было, а были цѣлые ряды тонкихъ глиняныхъ плитокъ, обожженныхъ и прочныхъ, расписанныхъ разными красками: это нарисованы буквы, фразы и цѣлыя сочиненія. Есть среди нихъ и сочиненія ариѳметическаго содержанія.

Обширная торговля, вмѣстѣ съ развитіемъ ремеслъ, заставила халдеевъ заняться практическими вычисленіями; этимъ любознательный народъ не удовольствовался и перешелъ къ теоретическимъ вопросамъ ариѳметики. Мало того, халдеи стали искать какихъ-то скрытыхъ, таинственныхъ свойствъ чиселъ, стали гадать на числахъ, волхвовать, предсказывать; цифрамъ придавался смыслъ символическій, и ими угадывали будущее. Какъ это бываетъ вездѣ и всегда, легковѣрные люди создали халдеямъ репутацію искусныхъ гадальщиковъ. Въ 139 г. до Р. X. они были изгнаны изъ Рима за волшебство. Но слава ихъ и вліяніе былн замѣтны еще въ средиіе вѣка въ Западной Европѣ, такъ что имъ приписываютъ особыя кабалистическія цифры, употреблявшіяся въ астрологіи (см. 7-е приложеніе).

Греки. Древнѣйшія цифры грековъ мы указали выше. Позднѣйшими цифрами, примѣрно за 100 лѣтъ до Р. X., стали служить буквы алфавита въ ихъ нормальномъ порядкѣ. Единицы, десятки и сотни обозначаются по этой системѣ такъ: 1=α, 2=β, 3=γ, 4=δ, 5=ε, 6=σ, 7=ζ, 8=η, 9=θ, 10=ι, 20=κ, 30=λ, 40=μ, 50=ν, 60=ξ, 70=ο, 80=π, 90=ς, 100=ρ, 200=ζ, 300=τ, 400=υ, 500=φ, 600=χ, 700=ψ, 800=ω, 900=ω̈. Тутъ, какъ видно, всего цифръ 27, а буквъ у грековъ въ алфавитѣ имѣется только 24; поэтому пришлось добавить къ нимъ еще 3 буквы старинныхъ, давно уже вышедшихъ изъ практики, такъ наз. vâv, koppa и sampi, для обозначенія 6, 90 и 900.

Чтобы отличить число отъ слова, греки проводили обыкновенно надъ цифрами черту, такъ, напр., ^—ι^—ε[4]=15,^—π^—χ^—β=122. Для обозначенія тысячъ они пользовались опять 9-ю первыми знаками, но подъ ними проводили маленькую вертикальную черту, напримѣръ, _|α=1000, _|β=2000, _|γ=3000, _|^—α^—φ^—ο^—ε=1575, _|^—ε^—τ^—π=5380, _|^—θ^—ω^—μ^—γ= 9843, _|^—γ^—χ^—ν^—δ=3654.

Десятокъ тысячъ составляетъ новую употребительную едииицу счета — миріаду. Греки любили пользоваться миріадами и прииѣняли ихъ съ такою же охотой, cъ какой мы примѣняемъ тысячи и милліоны; можно сказать, что въ греческомъ счисленіи классъ состоялъ изъ 4 разрядовъ, а не изъ 3-хъ, какъ въ нашемъ, такъ что при выговариваніи большихъ чиселъ они прежде всего указывали миріады, а послѣ нихъ и тысячи и остальные всѣ разряды. Знакъ миріады былъ М или Мν. Двѣ миріады обозначались черезъ βM.

Миріада миріадъ, по нашему сто милліоновъ, обозначалась черезъ Мβ. Миріада въ кубѣ, иначе сказать трилліонъ, писалась Мγ. Отдѣльаыя же миріады раздѣлялись точками, поэтому: Мγ.ε_|Mβ.ρι_|Mα._|εσπ=5601052800000. Какъ видно, цифры здѣсь располагаются отъ лѣвой руки къ правой, но это было не всегда, и такой порядокъ не считался обязательнымъ: можно было писать отъ правой руки къ лѣвой; въ Сициліи и Малой Азіи даже и выговариваніе чиселъ происходило отъ низшаго разряда къ высшему, такъ что сперва произносились единицы, затѣмъ десятки, сотни, тысячи и высшіе разряды.

Буквы — цифры гораздо менѣе удобны, чѣмъ выше упомянутые знаки Геродіана. Внося немало сбивчивости при письмѣ, онѣ, кромѣ того, мѣшаютъ производству дѣйствій, такъ какъ при нихъ надо въ отдѣльности учиться, какъ вычислять съ простыми единицами, въ отдѣльности съ десятками и съ прочими разрядами: нѣтъ аналогіи и мало сходства въ вычисленіяхъ съ отдѣльными разрядами.

Евреи. Они употребляли вмѣсто цифръ буквы алфавита. Очевидно, они это сдѣлали подъ вліяніемъ гречесжихъ ученыхъ, жившихъ въ Александріи, въ Египтѣ. Точно сказать нельзя, когда именно евреи перешли къ такой системѣ цифръ; но, вѣроятно, это случилось незадолго до Р. X., по крайней мѣрѣ, на еврейскихъ монетахъ такія цифры встрѣчаются не ранѣе 137 г. до Р. X.

Числа отъ 1 до 9 выражались у евреевъ первыми 9-ю буквами алфавита, круглые десятки (20, 30…. 90) девятью слѣдующими буквами, затѣмъ круглыя сотни— 100, 200, 300, 400 выражались четырьмя остальными, потому что въ еврейскомъ алфавитѣ было всего навсего 22 буквы. И вотъ для остальныхъ круглыхъ сотенъ буквъ недоставало. Первоначально этотъ недостатокъ пополнялся тѣмъ, что вмѣсто 500 писали 400+100, 600=400+200 и т. д. Потомъ догадались отсѣчь концы у 5 слишкомъ длинныхъ буквъ (Капхъ, Мемъ, Нунъ, Пхе, Тцаде) и этими концами начали обозначать остальныя сотни. Еврейскія цифры см. въ приложеніи 8-мъ, въ концѣ книги.

Тысячи обозначались опять при помощи 9 первыхъ буквъ, но только надъ ними ставились точки, чтобъ не смѣшать съ простыми единицами. Чтобъ отличить числа отъ словъ, употребляли въ первомъ случаѣ особый знакъ. Цифры писались отъ правой руки къ лѣвой, въ порядкѣ уменьшающейся величины значеній; слѣдовательно, разряды низшіе писались влѣво, а не вправо, какъ пишутся у насъ. Впрочемъ, у всѣхъ народовъ такъ наз. семитическаго корня, т.-е. евреевъ, вавилонянъ, арабовъ, финикіянъ, эфіоповъ, ассиріянъ, письмо шло противоположно нашему, т.-е. отъ правой руки къ лѣвой.

Сирийцы. Ихъ цивилизація относится къ гораздо болѣе позднѣйшимъ временамъ, чѣмъ финикійская, халдейская, египетская и т. д. Ихъ можно бы назвать въ нѣкоторомъ родѣ преемниками финикіянъ. По крайней мѣрѣ, въ III в. по Р. X. мы встрѣчаемъ у сирійцевъ цифры, которыя очень похожи на тѣ, какія были въ Финикіи за много лѣтъ до Р. X. Позднѣе эти цифры быди отброшены, и, начиная приблизительно съ VII в. по Р. X., сирійская литература содержитъ буквы алфавита вмѣсто цифръ. Здѣсь мы находимъ то же самое, что въ Греціи и у евреевъ. Сирійскій алфавитъ, какъ и еврейскій, содержитъ 22 буквы. Для выраженія простыхъ единицъ, круглыхъ десятковъ и сотенъ отъ 100 до 500, буквъ алфавита было достаточно, какъ видимъ мы и у евреевъ. 500, 600 и далѣе до 10001 сирійцы означали при помощи сложенія, такъ что 500=400+100, 600=400+200 и т. д. Круглыя тысячи они писали какъ простыя единицы, только внизу налѣво приписывали запятую. Значеніе десятковъ тысячъ давалось единицамъ и десяткамъ при помощи маленькой горизонтальной черточки, которою подчеркивались цифры. Значеніе милліона давалось 2-мя запятыми.

Славяне. Составитель славянскаго алфавита, св. Кириллъ, заимствовалъ систему цифръ цѣликомъ у грековъ. Какъ греки пользовались буквами своего алфавита, такъ и для славянъ была составленаі таблица, схожая даже до мелочей съ греческою. Напр., почему 2 обозначаетея по славянски черезъ вѣди, а не черезъ буки? Потому что въ греческомъ языкѣ нѣтъ отдѣльныхъ звуковъ «б» и «в», а есть для нихъ общая буква «вита» или «бета». Почему ѳита обозначаетъ девять, хотя ей мѣсто въ самомъ концѣ алфавита? Потому что въ греческомъ языкѣ ей соотвѣтствуетъ буква θ, которая и стоитъ здѣсь на своемъ мѣстѣ, а не въ концѣ алфавита. Червь, обозначающій 90, поставленъ вмѣсто коппы, такъ какъ по-гречески нѣтъ звука «ч» совсѣмъ, а по-славянски нѣтъ коппы. Вотъ рядъ славянскихъ цифръ:

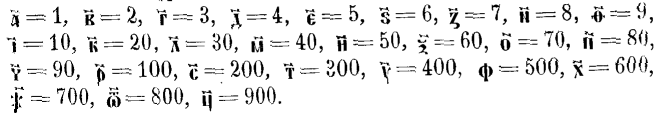Тысячи обозначаются тѣми же буквами, какими и единицы, но съ добавленіемъ значка, который ставится налѣво отъ цифръ, выражающихъ количество тысячъ. Вообще славянская система—полнѣйшая копія греческой: такъ же берутся буквы алфавита, похоже обозначаются тысячи, и даже есть наклонность къ счету миріадами, т. е. десятками тысячъ. Впрочемъ, большія числа въ старинныхъ рукописныхъ славянскихъ сборникахъ встрѣчаются не очень часто. Ниже, въ прилож. 9-мъ, приводимъ мы обозначенія большихъ количествъ: тьмы, легіона, леодра, врановъ. Эти изображенія встрѣчаются въ старинныхъ рукописяхъ грамматическихъ, но не ариѳметическихъ, такъ какъ въ ариѳметическихъ рукописяхъ 16–17 столѣтія предпочитаютъ пользоваться цифрами обыкновенными, которымъ мы даемъ названіе арабскихъ.

Римляне. Ихъ система цифръ не принадлежитъ къ числу удобныхъ и разработанныхъ. Римляне были слабы въ ариѳметикѣ, и даже до того слабы, что имъ никакъ не удалось освободиться отъ пережитковъ старой пятеричной системы счета, и только они одни остались при счетѣ пятками въ то время, какъ всѣ другіе народы, начавши, быть-можетъ, тоже со счета пятками, сумѣли выработать чистый счетъ десятками. Цифры у римлянъ смѣшанныя: однѣ изъ нихъ обязаны своимъ происхожденіемъ наглядности, а другія представляютъ собой буквы.

Римскія цифры таковы: I=1, V=5, X==10, L=50, C=100, D=500, М=1000. Изъ этихъ семи знаковъ легко можно составить обозначенія всѣхъ чиселъ. Тысяча иногда обозначалась не черезъ М, а черезъ (I), т. е. она обозначалась чертой среди 2 скобокъ. Согласно этому, и десятокъ тысячъ имѣлъ знакъ такой: ((I)), сто тысячъ (((I))), для милліоновъ брали ∞.

При помощи раздваиванія 3-хъ послѣднихъ знаковъ можно образовать 3 новыхъ цифры: І))=5000, І)))=50000, O | = 500000. Отсюда ясно видно, какъ получилось D для пятисотъ; это ничто иное, какъ тысяча (I), раздѣленная пополамъ, правая часть взята, а лѣвая откинута.

Значенія отдѣльныхъ знаковъ при письмѣ чаще всего складывались, напр., III=3, ХIII=13, MDCCCLXVI=1866. Но если высшій знакъ стоялъ правѣе низшаго, то это выражало отниманіе, такъ, напр., IX=9, XC=90. Вычитать обыкновенно можно было не больше одного знака, а прикладывать—не больше 3-хъ однородныхъ. Кромѣ того, прежде чѣмъ писать число, его разлагали на единицы, десятки, сотни и т. д., и чтобы написать хотя бы 990, писали сперва 900, затѣмъ уже 90, т.-е. CMXC, а не отнимали прямо отъ тысячи десятокъ. Бывали, впрочемъ, изрѣдка и исключенія: IIX=8, вмѣсто VIII; VIIII=9, вмѣсто IX; послѣдняя фигура (VIIII) была особенно употребительна на памятникахъ и плитахъ, потому что римляне любили точность, а между тѣмъ если подойти съ другой стороны, то IX покажется не 9-ю, а 11-ю (XI).

Только у однихъ римлянъ и видимъ мы отниманіе низшаго знака отъ высшаго, ни у какого другого народа нѣтъ подобнаго обыкновенія; если и ставился у другихъ народовъ низшій знакъ перед высшимъ, то онъ указывалъ обыкновенно на повтореніе, а не на отниманіе. Даже и въ произношеніи у римлянъ было вычитаніе, особенно же если вычиталось 2 или 1, такъ, напр., вмѣсто восемнадцати они говорили двадцать безъ двухъ. Только въ случаѣ тысячъ низшій знакъ показывалъ умноженіе и, напр., десять тысячъ можно было писать черезъ X M=10×1000, а сто тысячъ черезъ CM; въ послѣднемъ случаѣ являлась полная возможность смѣшать 100000 съ 900, потому что не видно было, надо ли 1000 взять сто разъ или же отнять 100 отъ 1000.

Точно такъ же писали иногда MM, и въ этомъ случаѣ опять не видно было, сколько тысячъ обозначено зтой формулой: или это двѣ тысячи (М+М), или тысяча тысячъ (М×М), и то и другое чтеніе имѣетъ свои основанія и можетъ считаться правильныиъ приходилось догадываться по смыслу, какое именно число надо подразумѣвать въ каждомъ отдѣльномъ случаѣ. Чтобы избѣжать сомнѣній и ошибокъ, римляне стали употреблять еще новый пріемъ по которому тысячи обозначались горизонтальной линіей вверху; этимъ пріемомъ 1000 пишется Ī, 100000=^—С,[5] 1000000=^—M, равнымъ образомъ ^—C^—C=200000, ^—C^—L^—X=160000.

Знакъ |¯| над цыфрами придавалъ имъ значеніе сотенъ тысячъ, такъ напримѣръ |^—X^—V^—I^—I | = 1700000, |^—M|= 1000^.100000 = 100 000 000. Знаменітый ученый и естествоиспытатель Плинiй (въ I вѣкѣ по Р. X.) ввелъ знакъ для тысячъ точку, слѣдовательно L.D=50500. Встрѣчаемъ и еще обозначеніе: Vm.=5000.

Теперь мы видимъ и ясно можемъ убѣдиться. насколько весь порядокъ нумераціи у римлянъ былъ сбивчивъ, непослѣдователенъ и могь представить много поводовъ къ толкованіямъ въ ту и другую сторону. Вѣрнѣе всего мы отъ римлянъ заимствовали обыкновеніе, чтобъ сумму денегъ въ разныхъ векселяхъ, распискахъ и т. д. писать не только цифрами, но и словами. Для римлянъ это было очень важно и настоятельно необходимо, потому что всѣ эти черточки при цифрахъ легко можно стереть, продолжить и пополнить. Исторія передаетъ намъ случай, когда изъ-за неясности написаннаго ряда цифръ произошелъ большой споръ относительно завѣщаннаго наслѣдства. Гальба получилъ отъ Ливіи Августы по завѣщанію 50 милліоновъ сестерцій (приблиз. 5 милліоновъ рублей), но Тиверій, главный наслѣдникъ, сумѣлъ доказать, что подъ этими цифрами надо разумѣть только 500 000 сестерцій; ему это удалось тѣмъ легче, чтс сумма денегъ не была написана словами.

При выговариваніи большихъ чиселъ у римлянъ не было въ распоряженіи другихъ словъ, кромѣ тысячи. Поэтому 1000 000 000 они читали такъ: тысячью тысяча разъ по тысячѣ.

Относительно происхожденія римскихъ цифръ существуетъ много различныхъ мнѣній и догадокъ. Нѣкоторые полагагюъ, что начало этимъ цифрамъ дано буквами стариннаго алфавита. Другіе объясняютъ такъ: первыя три цифры I, II и III само собой понятны: онѣ произошли отъ счета линій; цифра V образовалась изъ картины руки, т.-е. пяти пальцевъ, потому что, если бы очертить кисть руки съ раздвинутыми пальцами, то и получилась бы фигура, напоминающая цифру V; цифра десять своею формой косого креста разлагается на 2 пятка X приложенныхъ другъ къ другу острыми концами; «С», которое обозначаетъ сто, является первой буквой числительнаго «Centum», что значитъ сто; M—тысяча, это начальная буква латинскаго слова «Mille» (тысяча). О томъ, какъ получился знакъ пятисотъ D, нами уже сказано выше. Такъ же можно объяснить и знакъ пятидесяти L, именно сто [, а 50 = └, т.-е. знакъ ста раздвоенъ на двѣ половины, изъ которыхъ нижняя взята, а верхняя половина отброшена.