"Логические ошибки. Как они мешают правильно мыслить" - читать интересную книгу автора (Уемов Авенир)

4. Умозаключение

Суждения, так же как и понятия, не существуют сами по себе, вне связи с другими суждениями. Они связываются. между собой, образуя более сложные мысли, более сложные логические формы. Примеры такой связи суждений у нас уже были выше:

или:

Логическая форма, которую образует такого рода связь суждений, называется умозаключением. К умозаключениям относится и то преобразование двух разделительных суждений в одно условное, которое было только что проделано.

В чем же сущность умозаключения как логической формы? Далеко не всякая связь суждений будет умозаключением. Умозаключением являются лишь такие соотношения суждений, при которых истинность или ложность одних из этих суждений обусловливает истинность или ложность других. Так, истинность суждения «„Крым“ пишется с большой буквы» вытекает из истинности суждений «имена собственные пишутся с большой буквы» и «„Крым“ — имя собственное».

Если каждое суждение выражает то, что уже известно, то умозаключение — это такая сложная мысль, в которой на основе известного получается новое знание. Новое знание, то есть суждение, которое получается как результат умозаключения, называется заключением, или выводом. Суждения, из которых делается вывод, называются посылками. Так, в первом из наших умозаключений суждения «все млекопитающие дышат легкими» и «дельфин — млекопитающее» являются посылками, а суждение «дельфины дышат легкими» — выводом. Во втором умозаключении посылками будут суждения «имена собственные пишутся с большой буквы» и «„Крым“ — имя собственное», выводом же будет суждение «„Крым“ пишется с большой буквы».

Умозаключения, так же как понятия и суждения, бывают разных типов.

При делении умозаключений важнейшим является вопрос о том, откуда берется в умозаключении вывод, которого нет в посылках? На каком основании и в какой мере можно быть уверенным в том, что если посылки истинны, то заключение также будет истинно?

Мы можем получать вывод из посылок путем более или менее сложного преобразования последних. Выше был приведен пример такого преобразования, когда из двух разделительных суждений было получено условное.

Поскольку вывод здесь получается лишь на основе преобразования посылок, его истинность в данном случае целиком определяется истинностью посылок, если, разумеется, это преобразование производится правильно. Правила же этих преобразований в свою очередь, естественно, обусловливаются, как будет дальше показано, формой посылок. Умозаключения такого типа будем называть дедуктивными.

Рассмотрим вначале такие дедуктивные умозаключения, в которых вывод получается путем преобразования одной посылки. Возьмем суждения «Петя не является плохим мальчиком», «ваше утверждение неправильно» и преобразуем их таким образом: «Петя — неплохой мальчик», «ваше утверждение не является правильным», то есть передвинем отрицание со связки на предикат. В результате такого преобразования получились новые суждения, которые по своему содержанию хотя и незначительно, но все же отличаются от исходных: в первом усилилась похвала Пете, во втором — выражение смягчилось, стало более деликатным. С точки же зрения логической формы различие довольно существенное — изменилось качество суждений и предикат: отрицательная связка (Петя не есть плохой мальчик) заменена положительной (Петя есть неплохой мальчик) и предикат «плохой мальчик» заменился предикатом «неплохой мальчик» положительная связка (ваше утверждение есть неправильное) заменена отрицательной (ваше утверждение не есть правильное) и предикат «неправильное утверждение» заменен, предикатом «правильное утверждение». Такое преобразование посылок, при котором изменяется качество суждений и предикат, называется превращением. Превращение имеет большое значение, но не само по себе — отдельно оно встречается довольно редко, — а как составная часть других умозаключений.

Превращения, как мы видим, представляют собой преобразование одного суждения. Такого рода преобразование называется непосредственной дедукцией. К непосредственной дедукции наряду с превращением относится также обращение.

Обращение — это такое преобразование одного суждения, при котором субъект и предикат меняются местами. Например, суждение «некоторые щуки жили более 200 лет» в результате обращения преобразуется в суждение «некоторые существа, жившие свыше 200 лет, являются щуками»; «S есть P» изменяется в «P есть S», Еще пример: «никто из студентов нашей группы не сдал экзаменов досрочно». В этом суждении субъект (S) — «студенты нашей группы», предикат (P) — «сдавшие экзамен досрочно». Меняя местами субъект и предикат, получаем суждение «ни один из сдавших экзамены досрочно не является студентом нашей группы».

Значительно большую роль играют опосредствованные умозаключения, в которых вывод делается из нескольких, чаще всего из двух, посылок. К ним относятся прежде всего умозаключения, называемые силлогизмами (слово «силлогизм» по-гречески обозначает «умозаключение»). Существуют разные типы силлогизмов соответственно разным типам суждений, входящих в их состав. Наиболее распространенными являются три вида силлогизмов: категорические, разделительно-категорические и условно-категорические. Уже по самим этим названиям можно судить о составе каждого из этих трех разновидностей силлогизмов: категорические состоят из категорических (то есть простых — с одним субъектом и предикатом) суждений, разделительно-категорические — из разделительных и категорических, условно-категорические — из условных и категорических.

Остановимся на каждом из этих трех видов в отдельности.

В категорическом силлогизме посылками служат два простых категорических суждения. Именно к ним относятся приводившиеся выше образцы таких рассуждений, как:

или:

В чем специфика этого силлогизма? С помощью какого преобразования посылок получается здесь вывод?

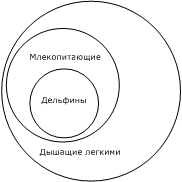
Мы уже знаем, что каждое категорическое суждение можно представить как отношение объемов понятий, входящих в суждение. Это в равной мере относится и к посылкам и к заключению. В заключении устанавливается определенное отношение между объемами понятий. Но на каком основании? На основании того отношения, которое дается в посылках. В посылке «все млекопитающие дышат легкими» класс млекопитающих включается в класс дышащих легкими; в другой посылке класс дельфинов включается в класс млекопитающих. Поэтому в заключении мы можем класс дельфинов включить в класс существ, дышащих легкими (рис. 7).

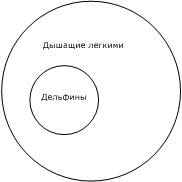В результате умозаключения понятие «млекопитающие» выпадает. Нас интересует в данном случае отношение дельфинов и существ, дышащих легкими; поэтому на основании посылок мы прямо выводим в заключении интересующее нас отношение «дельфины дышат легкими» (рис. 8).

Аналогичный процесс рассуждения имеет место и во всех других случаях умозаключений, называемых категорическими силлогизмами. Таким образом, всякий категорический силлогизм есть такое умозаключение, в котором определяется отношение объемов двух понятий на основании тех отношений между понятиями, которые даны в посылках.

Понятия, между которыми устанавливаются отношения в посылках и в заключении силлогизма, называются терминами. Понятия, которые входят в заключение, называются крайними терминами: субъект заключения — меньший крайний термин S, предикат заключения — больший крайний термин P.

В нашем примере меньшим термином будет «дельфин», большим — «существа, дышащие легкими».

Оба эти термина есть и в посылках; они связываются в заключении на основании того, что о них утверждается в посылках. Но в посылках есть еще понятие «млекопитающие», которого нет в заключении. Это понятие связывает в посылках крайние термины. В каждую посылку входит один из крайних терминов, и это третье понятие, которое называется средним термином, обозначается буквой M — первой буквой латинского слова «medius» — «средний». Посылка, в которую входит меньший термин, то есть субъект заключения, называется меньшей посылкой, а та, в которую входит больший термин, то есть предикат заключения, называется большей посылкой. Отметим, что меньший термин обозначается буквой S, а больший — буквой P не только в заключении, но и в посылках, несмотря на то что там S может не быть субъектом, а P может не быть предикатом.

Все категорические силлогизмы состоят из простых Категорических суждений. Но суждения, как мы знаем, могут быть и иного типа.

Разделительное суждение в сочетании с категорическим образует разделительно-категорический силлогизм, например:

При той же самой большей посылке меньшая может измениться; тогда силлогизм получит такой вид:

В первом силлогизме заключение имеет положительную связку, во втором — отрицательную. В связи с этим силлогизм первой формы называется утверждающим, силлогизм второй формы — отрицающим. Если представить их в общем виде с помощью букв, то получим следующие формулы разделительно-категорического силлогизма:

утверждающего

отрицающего

Преобразование посылок в утверждающем силлогизме заключается в том, что на основании меньшей посылки (S не есть ни P₁, ни P₂) исключаются все предикаты большей посылки, кроме одного (P₃), который отсутствует в меньшей, и он переходит в качестве предиката в заключение: S есть P₃. В отрицательной форме, наоборот, меньшая посылка (S есть P₁) как бы выбирает один из предикатов большей посылки, а заключение отбрасывает остальные: S не есть ни P₂, ни P₃.

Если сложное разделительное суждение в соединении с категорическим дает разделительно-категорический силлогизм, то соединение сложного условного суждения с категорическим образует силлогизм, называемый соответственно условно-категорическим, например:

или

В виде формул эти силлогизмы можно выразить следующим образом:

В первой формуле вывод (S₂ есть P₂) представляет собой записанное самостоятельно следствие условного суждения, являющегося первой посылкой.

Во второй формуле основание большей посылки (S₁ есть P₁) «человек заинтересован в результате своего труда» преобразуется в выводе в суждение с отрицательной связкой (S₁ не есть P₁) «Иванов не заинтересован в результате своего труда».

Одно из суждений, входящих в состав силлогизма, может быть опущено. Например:

Такого рода сокращенный силлогизм называется энтимемой (от древнегреческого «энти меме», что значит «в уме»).

Все рассмотренные виды умозаключений — превращение, обращение и разные виды силлогизмов — характеризуются одной общей чертой: во всех случаях вывод здесь получается путем преобразования исходных суждений, то есть посылок. Как правило, вывод в таких умозаключениях делается от общего к частному, но это не обязательно.

Однако далеко не во всех случаях можно получить вывод таким способом. Например, каким преобразованием посылок можно из истинности суждения «некоторые щуки жили свыше 200 лет» вывести ложность суждения «ни одна щука не жила свыше 200 лет»? Ясно, что преобразования посылок здесь недостаточно для получения вывода. Вывод здесь может быть получен лишь с помощью постороннего основания, которое должно быть дано помимо посылок.

Вопрос в данном случае заключается, не в том, правильно ли производятся преобразования посылок, а в том, применимо ли то или иное основание к данному случаю, связывает ли оно и как связывает посылки с заключением, в какой мере оно само правомерно.

В связи с тем, что правильные преобразования не могут из истинного положения сделать ложное и, наоборот, из ложного — истинное, дедукция всегда производится от истинности к истинности (то есть истинность посылок обусловливает истинность следствия) или от ложности к ложности (ложность посылок приводит к ложности заключения).

В умозаключениях же недедуктивного типа в отличие от дедуктивных можно получать выводы как от истинности к истинности и от ложности к ложности, так и от ложности к истинности и от истинности к ложности.

Среди умозаключений недедуктивного типа, как и в дедуктивных, можно выделить непосредственные умозаключения, то есть вывод из одной посылки.

К ним относятся, например, выводы от истинности одного суждения и ложности другого или, наоборот, от ложности к истинности. Эти выводы можно делать в том случае, когда имеются два суждения, из которых одно отрицает то, что говорится в другом. Например, суждение «некоторые грибы не съедобны» отрицает суждение «все грибы съедобны». Такие суждения называются противоречащими друг другу.

Метод, позволяющий делать выводы от одного суждения к другому, ему противоречащему, основывается на применении следующего положения: «Из двух противоречащих друг другу суждений одно истинно, другое ложно, третьей возможности не может быть». Как мы увидим дальше, это положение является одним из основных законов мышления.

С помощью этого положения можно делать выводы двух типов: 1) от истинности одного суждения к ложности другого, ему противоречащего, 2) от ложности одного суждения к истинности противоречащего ему. Например, если известно, что суждение «некоторые щуки жили свыше 200 лет» истинно, то отсюда можно сделать вывод о ложности противоречащего ему суждения «ни одна щука не жила свыше 200 лет». Или если суждение «все грибы съедобны» ложно, то противоречащее ему суждение «некоторые грибы не съедобны» будет истинным.

Из недедуктивных выводов, делающихся более чем из одной посылки, рассмотрим умозаключение по аналогии, или просто аналогию. Аналогия представляет собой вывод о свойствах какого-либо предмета на основании данных о другом предмете.

Известным примером умозаключения по аналогии будет вывод об обитаемости планеты Марс на основании обитаемости Земли.

Современная техника пока еще не позволяет совершать межпланетные путешествия. Однако это не означает, что мы должны отказаться от всяких выводов об обитаемости Марса. Здесь приходит на помощь умозаключение по аналогии. Не трудно заметить, что планета Марс обладает свойствами, общими со свойствами Земли. Как та, так и другая планета окружена атмосферой. На обеих планетах в атмосфере есть кислород в свободном виде. На той и другой планете есть вода. Обе планеты вращаются вокруг своих осей, которые наклонены к плоскости вращения Солнца. Благодаря этому на обеих планетах существует смена дня и ночи, времен года. Наконец, расстояния обеих планет от Солнца и время обращения вокруг него незначительно отличаются друг от друга. Близки и размеры планет: Марс немного меньше Земли. Все это дает основание для предположения о том, что обеим планетам будут общи и другие признаки, в частности признак обитаемости, и можно, следовательно, сделать вывод о том, что жизнь есть и на Марсе. Этот вывод будет получен путем умозаключения о свойствах одного единичного объекта (Марса) с помощью данных о свойствах другого единичного объекта (Земли), то есть путем умозаключения по аналогии.

Каковы же основания, с помощью которых можно связать посылки со следствием в умозаключении по аналогии? Эти основания могут быть различными, и в зависимости от этого вывод может быть мало вероятным, весьма вероятным или же вполне достоверным.

Если просто, исходя из наличия у двух данных предметов нескольких общих признаков, делать вывод о том, что у них обязательно будут общими и еще какие-нибудь признаки, то такое обоснование вывода было бы очень слабым и переход от посылок к следствию дал бы лишь самую малую вероятность истинности последнего.

Другое дело, когда таким основанием является общность не случайных, а наиболее существенных для обоих предметов признаков, а также существенность для них того признака, который переносится с одного предмета на другой. В этом случае об истинности следствия можно говорить с гораздо большей степенью вероятности.

Наконец, возможен и такой случай, когда вывод, получаемый с помощью аналогии, является вполне достоверным. Такой вывод аналогия дает при установлении следующей связи между признаками двух предметов: если два предмета (A и B) имеют ряд общих признаков (a, b, c, d…), то по наличию у одного из этих предметов (A) определенного признака (#946;) можно судить о том, что тот же признак (#946;) присущ и другому предмету (B).

В этом случае можно было бы составить такой условно-категорический силлогизм:

Таким образом, аналогия будет достоверна, поскольку достоверна дедукция. Например, пусть нам известно, что двум предметам присущи общие свойства — однородность, удельный вес, вес предмета в целом — и что один из этих предметов имеет объем, равный 5 м³. По аналогии делаем вывод о том, что другому предмету также присуще это свойство, то есть объем в 5 м³. Достоверен ли этот вывод? Достоверен, так как в данном случае между признаками предметов существует та связь, о которой говорилось выше. Еще пример: два человека имеют общих родителей; бабушку одного из них зовут Марией Петровной; по аналогии заключаем, что бабушку второго также зовут Марией Петровной.

Такого рода рассуждения по аналогии особенно часто применяются в юриспруденции. Если, например, преступления, совершенные двумя преступниками (A) и (B), одинаковы, то у них одинаковы все признаки, интересующие суд (a, b, c, d…). Одному из преступников (A) вынесен приговор #946;. Следовательно, другому преступнику (B) должен быть вынесен тот же самый приговор #946;.

Все сказанное отнюдь не означает, что достоверная аналогия в отличие от недостоверных выводов по аналогии является дедукцией. Структура умозаключения во всех случаях аналогии совершенно одинакова:

Структура, строение умозаключения — это главное основание при классификации логических форм. Как в недостоверной, так и в достоверной аналогии мы, переходя от посылок к следствию, опираемся на общее положение — принцип. Разница только в том, что в первом случае это положение представляет собой лишь вероятное суждение, во втором же — вполне достоверное. Во всех случаях умозаключений по аналогии основной задачей в отличие от дедукции будет выяснение того, на какое именно основание можно опереться, в данном случае — основание, которое в посылках не дано. Дедукция заключается только в преобразовании данных посылок. В связи с этим правомерность вывода в дедукции определяется правомерностью преобразования посылок, тогда как в аналогии правомерность вывода определяется истинностью того основания, при помощи которого удается связать посылки с заключением.