"В поисках похищенной марки" - читать интересную книгу автора (Левшин Владимир Артурович)
ДВАДЦАТЬ ЧЕТВЁРТОЕ ЗАСЕДАНИЕ КРМ
решили провести на свежем воздухе, так сказать шутя-гуляючи. День был морозный, солнечный. Приятно было не спеша пройтись по тихим переулкам старого Арба#769;та.
Так уж получилось, что это заседание стало как бы продолжением предыдущего, внеочередного: оно началось с разбора любопытных числовых зависимостей.
— Как вы думаете… — спросил президент, который шёл пятясь, чтобы видеть всю нашу компанию разом. — Как вы думаете, какое число меньше: 165 или 732? — И тут же. сам себе ответил: — Ясно, 165. Значит, Магистр не ошибся, выбрав верблюда с табличкой «165». А Единичка и впрямь транжирка.
Тут он наскочил на прохожего и долго извинялся, после чего продолжал путь более удобным способом.
— Не забывай, — сказала Таня, — что 165 вовсе не обозначало плату за проезд. Чтобы узнать цену, надо было с этим числом произвести ещё целый ряд манипуляций.
— Хоть бы и так, — хорохорился Нулик. — Все равно самое большое число, которое получится от перестановок цифр в числе 165, это 651. А 651 как-никак меньше, чем число 732, которое выбрала Единичка!
— А ведь правда… — раздумчиво протянул Сева. — Даже наименьшее число, которое получается от перестановок цифр 7, 3 и 2, — число 237 и то больше числа 165.
— Эх вы, теоретики! — поддразнила Таня. — Лучше подсчитайте, что должен был заплатить Магистр за своего верблюда и что Единичка — за своего.
— Это мы могим! — весело согласился президент и принялся писать веточкой на снегу. — Сперва сделаем все возможные перестановки цифр в числе 165. Вот они: 165, 156, 561, 516, 651 и 615. Теперь сложим эти числа. Получим… Не мешайте, а то я собьюсь… получим 2664. Проверим…
— И проверять нечего, все верно, — торопила Таня.
— Теперь подсчитаем, что должна была заплатить Единичка, — сказал Сева. — Вот перестановки цифр числа 732: 732, 723, 273, 237, 327 и 372. Сложим их и получим… что такое! Тоже 2664.
— В чём же дело? — недоумевал президент. — Выходит, в этом случае любое трехзначное число даст один и тот же результат? Или, может быть, 165 и 723 — числа специально подобранные?
— Уж конечно, специально, — сказала Таня.
— Вот это да! Значит, проезд на любом верблюде стоил одинаково. Но как же удалось подобрать такие числа?
— А ты посмотри на них внимательней, — посоветовала Таня. — Не найдётся ли у них какого-нибудь общего признака?
— Найдётся! — отвечал президент весьма язвительно. — Все цифры у них разные.
— Цифры действительно разные, — подтвердила Таня, — зато сумма этих цифр одна и та же: 12.
— Верно! — обрадовался Нулик. — 1+6+5=12. И 7+3+2 тоже равно двенадцати. Может быть, то же свойство было и у всех других чисел на верблюжьих табличках?
— Очень возможно. Недаром Единичка сказала, что погонщики в Террапантере — народ справедливый.
— И всё-таки… — Нулик сделал непреклонное лицо, — всё-таки я требую доказательства.
— Сей момент, ваше президентство! — насмешливо поклонилась Таня. — Будет сделано. Запишем любое трехзначное число в общем виде. Это 100
— Что за вопрос? Конечно! Здесь
— Гениально! Теперь сделаем в этом числе все возможные перестановки цифр. Напишем их сразу столбиком, а потом сложим:
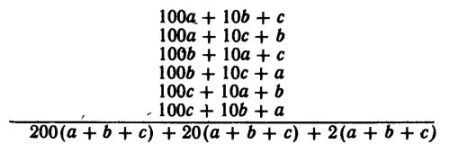 |
Не желаете ли, ваше президентство, преобразовать эту сумму? — спросила Таня.
— Желаю, — отвечал его президентство без особого энтузиазма. — Я бы… я бы вынес 2(
— Совершенно с вами согласна. Получится при этом
2(
— А это все равно что 222(
— Только то, что сумма перестановок зависит не от самого числа, а от суммы его цифр. И значит, все трехзначные числа с одинаковой суммой цифр в этом случае всегда будут давать одно и то же число.
— Ха-ха! — выдохнул президент, несколько подавленный роскошным Таниным доказательством. — Выходит, для всех трехзначных чисел с суммой цифр, равной двенадцати, ответ будет всегда 222*12, то есть 2664. Теперь хорошо бы ещё узнать, что получится, если взять четырех-, пяти- или двенадцатизначные числа…
— Да то же самое, — сказала Таня, — только численный результат будет другой.
— Обязательно займусь этим на досуге! Жаль, досуга у меня маловато, — проворчал Нулик, постукивая ногой об ногу и выразительно поглядывая на уютные окна кафе, мимо которого мы как раз проходили.
Это было понято, как безмолвный сигнал к атаке, и через мгновение мы уже находились внутри, за стеклянной дверью.
В кафе было тепло и, к счастью, безлюдно. Я говорю — к счастью, потому что Нулик, предвкушая лакомое угощение, взыграл и принялся носиться между столиками, описывая вокруг них замысловатые фигуры.
— Это я плутаю по лабиринту, — объяснил он, — скоро доберусь до мини-Тавра. Только вот где найти цепочку Афродиты?
Олег комически схватился за голову.
— Опять этот младенец повторяет ошибки Магистра!
— Ничуть не бывало! — выкрутился президент. — Просто я вас подначиваю. Из педагогических соображений…
Олег понимающе кивнул.
— Из педагогических, говоришь? Ну, тогда тебе, стало быть, известно, что произносить надо Минота#769;вр. И это тебе не мини, а совсем даже наоборот: огромное чудище. Получеловек, полубык.
— А разве такие бывают? — наивно спросил Нулик, сразу позабыв о педагогических соображениях.
 |
— Если верить древнегреческому мифу, один, во всяком случае, имелся. В давние времена, на острове Крит, у царя Мино#769;са. Этот самый Минос построил на Крите такой лабиринт, что выбраться оттуда не было никакой возможности. Здесь и поселил царь своего прожорливого и свирепого человеко-быка, а в пищу ему отправлял провинившихся и обречённых в жертву богам людей. Плутая по запутанным коридорам, те в конце концов неминуемо попадали в пасть к Минотавру.
— Безобразие! — возмутился Нулик. — Неужели никто с этим чудищем не справился?
— Представь себе, такой человек нашёлся. Звали его Тезе#769;й.
— Тезей… — повторил Нулик, хихикнув. — Тезей-ротозей…
— То-то и оно, что не ротозей. Тезей сумел-таки разделаться с Минотавром и выбрался из лабиринта.
— С помощью цепочки Афродиты?
— Да нет, греческая богиня Афродита тут ни при чём. Помогла Тезею дочь Миноса — Ариа#769;дна. Она дала ему клубок ниток. Тезей как вошёл в лабиринт, так сразу стал разматывать этот клубок. А когда победил Минотавра, пошёл обратно вслед за нитью, сматывая её по пути. Так нить вывела его на свободу. Отсюда и пошло выражение «нить Ариадны» — нить, которая помогает выбраться из запутанных, затруднительных обстоятельств.
Президент озабоченно поджал губы.
— Теперь без катушки ниток в кармане шагу не сделаю! Мало ли что…
Опасения его были прерваны официанткой, которая спросила, что нам принести. Я заказал кофе, слоёных пирожков и трубочек с кремом.
Нулик опасливо зыркнул глазом.
— Боюсь, у меня на такой пир пресмыкающихся не хватит.
— Чего-чего? — недоуменно переспросил Сева.
— Ну, скарабеев, — объяснил президент и очень обиделся, когда все дружно захохотали.
— Нет, он меня уморит! — сказал Сева, утирая глаза. — Какие же скарабеи — пресмыкающиеся? Они же вовсе насекомые. Попросту навозные жуки. А их, между прочим, в Древнем Египте считали священными и потому изображали на кольцах, печатях, всяких амулетах. Считалось, что скарабей приносит счастье…
 |
— Да ну?! — Президент даже подпрыгнул. — Хочу скарабея, хочу скарабея!.. — затараторил он, как Буратино.
Пришлось мне призвать его к порядку:
— Ты где находишься?
— В кафе.
— Так и веди себя соответственно. А хочешь говорить, так говори что-нибудь дельное. Вот хоть разберись в задаче со скарабеями.
Но охота говорить у президента почему-то разом прошла, и за дело взялся Сева. Выступление его было кратким — оно и понятно: он решал задачу алгебраическим способом.
— Число скарабеев, принесённых Черным Львом, обозначим буквой
— …(
— Верно. А так как у Мистера-Твистера Джерамини отнял в три раза больше скарабеев, чем у Чёрного Льва, число это равно 3
Нулик надулся.
— Да, оставили мне самое неинтересное…
Но всё-таки обиженно засопел над блокнотом:
— Переносим неизвестные в одну часть равенства, а известные — в другую. Тогда 2
— Так, — кивнул Сева. — А какую часть своей добычи отдал Шейк-Твист?
— Не беспокойся, подсчитаем и это! — бодро пообещал Нулик. — Если x=1/2
— Не совсем, — сказала Таня. — Остаётся узнать, во сколько раз у Джерамини оказалось денег больше, чем у обоих полицейских, вместе взятых.
— Узна#769;ем и это, — заверил её Сева. — У каждого из обделённых осталось по 1/2
Тут пришла официантка и все принялись за еду.
— Глядите-ка, — сказал вдруг Олег, вертя в пальцах бумажную салфетку. — Эта салфеточка нам как нельзя кстати. Она словно нарочно сделана для третьей задачи Магистра о треугольных галстуках. Ведь она сама треугольная!
Нулик грустно посмотрел на недоеденное пирожное.
— Ничего, старина! — утешил его Олег. — В конце концов, есть и решать задачу можно одновременно. В общем, Единичке нужно было разделить большой треугольный лоскут на пять небольших треугольников так, чтобы площади их относились, как 1:2:2:3:4.
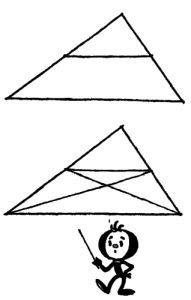 |
Он вынул карандаш и соединил середины боковых сторон треугольника, иначе говоря, провёл на салфетке одну из средних линий треугольника.
— Что у нас получилось? — спросил Олег. — Средняя линия разделила треугольник на две части. Одна из этих частей тоже треугольник, другая — трапеция. Все знают (а кто не знает, пусть докажет это сам), что площадь этого нового маленького треугольника в три раза меньше площади трапеции. Теперь проведём обе диагонали трапеции. Обратите внимание на то, что диагонали эти по совместительству представляют собой и медианы большого треугольника. Ведь они проведены в середине его боковых сторон! Все видят, что диагонали разделили трапецию на четыре части — на четыре треугольника. Самый маленький из них — верхний, два боковых — немного побольше, а самый большой — нижний. Узна#769;ем, каковы площади этих треугольников.
— Узна#769;ем! — решительно повторил Нулик, но тут же, впрочем, замолчал.
— Во-первых, нетрудно доказать (и пусть каждый опять-таки сделает это сам), что оба боковых треугольника равновелики, то есть имеют одинаковые площади. Во-вторых, приняв площадь самого маленького из этих четырех треугольников за единицу, выясним, во сколько раз каждый из остальных больше са#769;мого маленького.
Сева хлопнул себя по#769; лбу.
— Стоп! Кажется, нашёл. Ведь медианы треугольника делятся в точке пересечения на части, которые относятся, как 1:2. Так? А так как высоты самого маленького треугольника и любого из боковых одинаковы, то площади их тоже относятся, как 1:2.
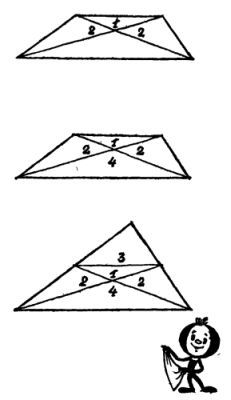 |
— Не в бровь, а в глаз! — констатировал Олег. — Бо#769;льшая часть задачи, таким образом, решена. Остаётся выяснить, во сколько раз площадь нижнего, самого большого треугольника больше площади самого маленького, принятого за единицу.
— И это тоже нетрудно! — подхватил Сева. — Ведь средняя линия, как известно, равна половине основания. А так как нижний и верхний треугольники, входящие в трапецию, подобны, то и высоты их тоже одна вдвое меньше другой. Ну, а раз так, то площади обоих треугольников относятся, как 1:4. Вот трапеция и разделилась на треугольники, площади которых относятся, как 1:2:2:4.
— Отлично! — сказал Олег. — Далеко пойдёте, молодой человек! А теперь ещё одно небольшое усилие: надо вспомнить, во сколько раз площадь первого отделённого нами треугольника меньше площади трапеции.
— Это я и без всяких усилий помню, — сказал Нулик. — Площадь отделённого треугольника меньше площади трапеции в три раза. Теперь подсчитаем, из скольких единиц состоит площадь трапеции. Площадь самого маленького мы приняли за единицу. Прибавим к этому два равных треугольника, площади которых вдвое больше, получим пять единиц. Теперь прибавим к этому площадь самого большого из четырех треугольников, равную четырём единицам. И получим всего девять единиц. Ну а 9, делённое на 3, опять-таки 3. Это и есть площадь первого отделённого нами треугольника.
— Молодчина! — одобрил Сева. — Теперь уж мы наверняка знаем, что площадь всего треугольника разделена на пять треугольников, площади которых относятся, как 1:2:2:3:4. Умница Единичка! Здо#769;рово решает задачи!
— Ура! — провозгласил президент и неожиданно, безо всякого перехода, похлопал себя по круглому пузику: — Ну и наелся же я!. Прямо как Пантагрюа и Гаргантюэль…
— Осади назад! — остановил его Сева. — С вашего позволения, не Пантагрюа и Гаргантюэль, а Гаргантюа#769; и Пантагрюэ#769;ль. Именно так называется книга Франсуа#769; Рабле. Только читать тебе её, пожалуй, рановато. Всякому овощу…
Нулик только досадливо отмахнулся и очень недовольный вылез из-за стола. И то сказать: невелика радость, когда тебе на каждом шагу напоминают, что ты ещё маленький…
Удивительно быстро темнеет зимой! Когда мы вышли из кафе, на улицах уже зажглись фонари. Падал тихий, лёгкий снежок. Мы снова свернули в малолюдный переулок.
Нулик не выдержал, побежал. За ним принялись бегать остальные.
— Догоняй! — крикнула Таня, пробегая мимо президента.
Тот с весёлым визгом помчался за ней. Вот он уже почти касается её рукой… Вдруг Таня круто остановилась и подалась в сторону. В следующее мгновение президент растянулся на тротуаре.
— Это все она виновата! — жаловался он, потирая ушибленную коленку.
— Ничего, — сочувственно сказал Сева, — девчонки, брат, они все такие…
— Да нет, — неожиданно захихикал Нулик, — я не про Таню, а про центробежную силу.
И опять все грохнули.
— Нанялся ты, что ли, повторять Магистровы нелепицы? — недоумевал Сева. — Бежал по тротуару по прямой линии, потом неожиданно остановился и упал, — ну при чём тут, скажи на милость, центробежная сила?
— А при том, что если бы я бежал не с такой силой, я бы не упал.
— Эх, ты! Мыслитель! Центробежная сила проявляется только тогда, когда тело движется по кривой — ну, скажем, по кругу. Вот едешь ты, например, в такси, и водитель на полной скорости резко разворачивается. И валишься ты при этом набок. Прижимает тебя к боковой стенке машины.
— Или ещё, — вспомнила Таня. — Ты крутишь над головой камень, привязанный к верёвке. Крутишь все быстрей и быстрей, и верёвка при этом натягивается все больше и больше, как струна. И опять здесь виновата центробежная сила. А если ты уж слишком сильно раскрутишь верёвку, она может и разорваться.
— Понял, понял! — закричал Нулик. — Верёвка разорвётся потому, что камешек будет рваться прочь от центра. Отсюда, наверное, и название — центробежная сила! Так?
— Так, да не так, — сказал я.
Ребята удивлённо переглянулись.
— Понятие центробежной силы возникло в восемнадцатом веке. Ввёл его французский учёный д'Аламбе#769;р. Но силу эту он правильно назвал фиктивной, то есть воображаемой.
— Значит, на самом деле центробежной силы не существует?
— И да и нет. Д'Аламбер придумал это понятие для того, чтобы удобнее было изучать движение тела по кривой.
— Чепуха какая-то! — рассердился президент. — Сила воображаемая, а верёвку разорвала!
— Ну, это дело тонкое. В двух словах не объяснишь. Опять-таки — всякому овощу своё время. А что касается Магистра, то он просто-напросто забыл закон Нью#769;тона. Забыл о том, что всякое тело стремится сохранить либо покой, либо прямолинейное равномерное движение. Это свойство тел называется инерцией. И когда Единичка, которая тянула Магистра за руку, внезапно остановилась, тот, все ещё продолжая двигаться по инерции, споткнулся и чуть было не упал.
— Наверное, по той же причине он и с верблюда свалился? — предположил президент.
— Ну нет! Если он и свалился с верблюда, то совсем не поэтому.
— Так отчего же?
— Чего не знаю, того не знаю. Может быть, просто заснул и ему все это приснилось. Потому что наяву было бы совсем иначе. Как бы высоко Магистр ни подпрыгнул в седле, опускаясь, он неизбежно снова шлёпнулся бы обратно в седло. И дело тут все в той же инерции. Подпрыгнув, Магистр одновременно продолжал бы двигаться по инерции в том же направлении и с той же скоростью, что и верблюд.
— С верблюдами наш дорогой математик вообще что-то напутал, — сказал Сева. — Ведь верблюды эти, по всему видно, были из породы дромадеров: недаром они шли в Сьеррадромадеру! А у дромадера всего только один горб. Так что сидеть между двумя верблюжьими горбами Магистр никак не мог.
— Это что! — вспомнил президент. — Он ведь ещё уверял, что на вокзале были верблюды с любым количеством горбов. А у них сроду больше двух не бывает…
— Бедные дромадеры! — вздохнул Олег. — Вот и доказывай после этого, что ты верблюд!
| © 2024 Библиотека RealLib.org (support [a t] reallib.org) |