"Фейнмановские лекции по физике. Выпуск 1. Современная наука о природе. Законы механики." - читать интересную книгу автора (Р. Фейнман, Р. Лейтон, М. Сэндс)
 |
K читателям русского издания
Это лекции по общей физике, которые читал физик–теоретик. Они совсем не похожи ни на один известный курс. Это может показаться странным: основные принципы классической физики, да и не только классической, но и квантовой, давно установлены, курс общей физики читается во всем мире в тысячах учебных заведений уже много лет и ему пора превратиться в стандартную последовательность известных фактов и теорий, подобно, например, элементарной геометрии в школе. Однако даже математики считают, что их науке надо учить по–другому. А уж о физике и говорить нечего: она столь интенсивно развивается, что даже лучшие педагоги все время сталкиваются с большими трудностями, когда им надо рассказывать студентам о современной науке. Они жалуются, что им приходится ломать то, что принято называть старыми или привычными представлениями. Но откуда берутся привычные представления? Обычно они попадают в молодые головы в школе от таких же педагогов, которые потом будут говорить о недоступности идей современной науки. Поэтому прежде чем подойти к сути дела, приходится тратить много времени на то, чтобы убедить слушателей в ложности того, что было ранее внушено им как очевидная и непреложная истина. Было бы дико сначала рассказывать школьникам «для простоты», что Земля плоская, а потом, как открытие, сообщать о ее шарообразности. А так ли далек от этого абсурдного примера тот путь, по которому будущие специалисты входят в современный мир идей теории относительности и квантов? Осложняет дело также то обстоятельство, что большей частью лектор и слушатели – люди разных поколений, и лектору очень трудно уйти от соблазна вести слушателей той знакомой и надежной дорогой, по которой он сам в свое время дошел до желанных высот. Однако старая дорога не вечно остается лучшей. Физика развивается очень быстро, и, чтобы не отставать от нее, надо менять пути ее изучения. Все согласны с тем, что физика – одна из самых интересных наук. В то же время многие учебники физики никак не назовешь интересными. В таких учебниках изложено все, что следует по программе. Там обычно объясняется, какую пользу приносит физика и как важно ее изучать, но из них очень редко можно понять, почему заниматься физикой интересно. А ведь эта сторона вопроса тоже заслуживает внимания. Как же можно сделать скучный предмет и интересным и современным? Об этом прежде всего должны подумать те физики, которые сами работают с увлечением и умеют передать это увлечение другим. Пора экспериментов уже наступила. Цель их – найти наиболее эффективные способы обучения физике, которые позволили бы быстро передать новому поколению весь тот запас знаний, который накоплен наукой за всю ее историю. Поиски новых путей в преподавании также всегда были важной частью науки. Преподавание, следуя развитию науки, должно непрерывно менять свои формы, ломать традиции, искать новые методы. Здесь важную роль играет то обстоятельство, что в науке все время происходит удивительный процесс своеобразного упрощения, который позволяет просто и кратко изложить то, что когда–то потребовало много лет работы.
Чрезвычайно интересная попытка в этом направлении была предпринята в Калифорнийском Технологическом институте (США), который сокращенно называют КАЛТЕХ, где группа профессоров и преподавателей после многочисленных дискуссий разработала новую программу по общей физике, а один из участников этой группы, крупный американский физик Ричард Фейнман, прочел лекции.
Лекции Фейнмана отличаются тем, что они обращены к слушателю, живущему во второй половине XX века, который уже многое знает или слышал. Поэтому в лекциях не тратится время на объяснение «ученым языком» того, что и так известно. Зато в них увлекательно рассказывается, как человек изучает окружающую его природу, о достигнутых сегодня границах в познании мира, о том, какие проблемы наука решает сегодня и будет решать завтра.
Лекции читались в 1961–1962 и 1962–1963 учебных годах; они записывались на магнитофон, а потом (и это оказалось само по себе трудной задачей) «переводились» на «письменный английский» профессорами М. Сэндсом и Р. Лейтоном. В этом своеобразном «переводе» сохранены многие особенности живой речи лектора, ее живость, шутки, отступления. Однако это очень ценное качество лекций отнюдь не было главным и самодовлеющим. Не менее важным были созданные лектором оригинальные методы подачи материала, в которых отразилась яркая научная индивидуальность автора, его точка зрения на пути обучения студентов физике. Это, разумеется, не случайно. Известно, что и в своих научных работах Фейнман всегда находил новые методы, которые очень быстро становились общепринятыми. Работы Фейнмана по квантовой электродинамике, статистике принесли ему широкое признание, а его метод – так называемые «диаграммы Фейнмана» – используется сейчас практически во всех областях теоретической физики.
Что бы ни говорили об этих лекциях – восторгались стилем изложения или сокрушались по поводу ломки старых добрых традиций, – одно остается бесспорным: надо начинать педагогические опыты. Наверное, не все согласятся с манерой автора излагать те или иные вопросы, не все согласятся с оценкой целей и перспектив современной физики. Но это послужит стимулом к появлению новых книг, в которых получат отражение другие взгляды. Это и есть эксперимент.
Но вопрос состоит не только в том, что рассказывать. Не менее важен и другой вопрос–в каком порядке это надо делать. Расположение разделов внутри курса общей физики и последовательность изложения – вопрос всегда условный. Все части науки настолько связаны друг с другом, что часто трудно решить, что надо излагать сначала, а что потом.
Однако в большинстве вузовских программ и имеющихся учебников до сих пор сохраняются определенные традиции.
Отказ от привычной последовательности изложения – одна из отличительных особенностей фейнмановских лекций. В них рассказано не только о конкретных задачах, но и о месте, которое занимает физика в ряде других наук, о путях описания и изучения явлений природы. Вероятно, представители других наук – скажем, математики – не согласятся с тем местом, которое отводит этим наукам Фейнман. Для него, как физика, «своя» наука, конечно, выглядит самой главной. Но это обстоятельство не занимает много места в его изложении. Зато в его рассказе ярко отражаются те причины, которые побуждают физика вести тяжелую работу исследователя, а также те сомнения, которые у него возникают, когда он сталкивается с трудностями, кажущимися сейчас непреодолимыми.
Молодой естествоиспытатель должен не только понять, почему интересно заниматься наукой, но и почувствовать, какой дорогой ценой достаются победы и как порой бывают тяжелы дороги, к ним ведущие.
Надо также иметь в виду, что если сначала автор обходился без математического аппарата или использовал лишь тот, который изложен в лекциях, то от читателя, по мере продвижения его вперед, будет требоваться увеличение его математического багажа. Впрочем, опыт показывает, что математический анализ (по крайней мере его основы) выучивается сейчас легче, чем физика.
Лекции Фейнмана вышли в США в трех больших томах. Первый содержит в основном лекции по механике и теории теплоты, второй – электродинамику и физику сплошных сред, а третий – квантовую механику. Чтобы книга была доступна большему числу читателей и чтобы ею было удобнее пользоваться, русское издание будет выходить небольшими выпусками. Первые четыре из них соответствуют первому тому американского издания.
Кому будет полезна эта книга? Прежде всего – преподавателям, которые ее прочтут целиком: она заставит их задуматься об изменении сложившихся взглядов на то, как начинать обучать физике. Далее, её прочтут студенты. Они найдут в ней много нового в дополнение к тому, что они узнают на лекциях. Конечно, ее попытаются читать и школьники. Большинству из них будет трудно одолеть все, но и то, что они смогут прочесть и понять, поможет им войти в современную науку, путь в которую всегда бывает трудным, но никогда не бывает скучным. Тому, кто не верит, что может пройти его, не стоит браться за изучение этой книги! И, наконец, ее могут читать все остальные. Читать просто так, для удовольствия. Это тоже очень полезно. Фейнман в своем предисловии оценивает результаты своего опыта не очень высоко: слишком малая доля студентов, прослушавших его курс, усвоили все лекции. Но так и должно быть.
Первый опыт редко приносит полный успех. Новые идеи всегда находят вначале лишь немного сторонников и лишь постепенно становятся привычными.
Январь 1965
ПРЕДИСЛОВИЕ Р. ФЕЙНМАНА
 |
Это – лекции по физике, которые я читал в прошлом и позапрошлом годах в Калифорнийском Технологическом институте для студентов первого и второго курсов. Но это не дословная их запись. Их пригладили – местами очень сильно, а порой не очень. К тому же это лишь часть полного курса обучения. Дважды в неделю 180 слушателей собирались в большой аудитории и, прослушав лекцию, группами по 15–20 человек проводили еще семинары под руководством ассистентов. Вдобавок раз в неделю проводились и лабораторные работы.
Чего мы хотели добиться, читая эти лекции? Мы хотели утвердить интерес к физике у молодых ее энтузиастов, у вчерашних выпускников средней школы. Перед поступлением в институт они много наслышались о том, как интересна и как увлекательна современная физика – теория относительности, квантовая механика и т. д. Но если бы этот курс читался так, как он читался раньше, весь их энтузиазм за два года мало–помалу улетучился бы – чересчур уж редко при обычном обучении встречаются действительно величественные, новые, современные идеи. Студентов заставили бы изучать наклонную плоскость, электростатику и прочее в этом роде, и все их порывы были бы сведены на нет. И весь вопрос был в том, сможем ли мы так построить курс, чтобы у самых способных, самых горячих студентов сохранился и укрепился их энтузиазм.
Не сочтите эти лекции каким–то обзорным курсом. Нет, курс этот весьма серьезен. Читая его, я ориентировался на самых сообразительных, я хотел по возможности, чтобы даже самые сильные слушатели не были в состоянии до конца усвоить все, что есть в этих лекциях. Для этого я подкидывал им мысли о возможных применениях основных идей и понятий вне основной линии наступления. Для этой цели я старался поточнее формулировать все утверждения, указывать, где только можно, какие уравнения и идеи укладываются в физическую картину мира и как при дальнейшем углублении они могут измениться. Я понимал также, что таким студентам очень важно указать, что из изучаемого они (если, конечно, у них достанет соображения) могут сами вывести из уже известного, а что, наоборот, для них совершенно ново. Формулируя новые идеи, я пытался либо вывести их, если они могли быть выведены, либо объяснить, что это действительно новая идея, что на уже изученные понятия ее опереть никак нельзя и что поэтому нельзя ее считать доказуемой, а можно лишь включить со стороны.
Приступая к лекциям, я предполагал, что студенты все же кое–что вынесли из средней школы – разные там геометрические оптики, простенькие понятия из химии и тому подобное. Я не видел также смысла в том, чтобы устанавливать какой–то определенный порядок в лекциях, чтоб нельзя было упоминать о вещах, о которых подробно будет говориться только позже. Наоборот, я часто вкратце говорю о том, что студент по–настоящему изучит намного позднее, когда он будет лучше подготовлен. Например, понятие об индуктансе или об энергетических уровнях дается на первых порах очень приблизительное и только спустя много времени развивается как следует.
Рассчитывая курс на самого активного слушателя, я все же учел интересы и такого парня, которого все эти фейерверки мыслей и многосторонние приложения могут только встревожить и отпугнуть, от кого вообще нельзя ожидать, что он усвоит большую часть материала. Я хотел, чтобы для него в лекциях оказалось по крайней мере основное ядро, или костяк, того, что он
Была у меня одна серьезная трудность, когда я читал эти лекции: не работала обратная связь – от студента к преподавателю; я не видел, насколько хорошо эти лекции доходят. Это очень серьезная помеха, и я поныне не знаю, хороши ли эти лекции. Это по существу эксперимент, и, если бы мне пришлось его проделать еще раз, я бы его поставил иначе, но я надеюсь, что мне не придется браться за это дело вторично! И все же мне кажется, что для первого курса, по крайней мере в отношении физики, все выглядит вполне прилично.
А вот второй частью курса я не очень доволен. В начале этой части, говоря об электричестве и магнетизме, я не смог придумать какого–либо особого, отличного от общепринятого способа изложения, не смог найти такого подхода к теме, который возбуждал бы к ней интерес. С электричеством и с магнетизмом, таким образом, не много мне удалось сделать. После этой темы в конце второго курса я сначала собирался прочесть несколько лекций о свойствах твердых тел, касаясь главным образом таких вещей, как нормальные колебания, решения уравнения диффузии, колебательные системы, ортогональные функции и т. д., т. е. изложить начала того, что обычно именуют «методами математической физики». Задним числом могу сознаться, что, если бы я решился читать этот курс вторично, я бы непременно вернулся к этому намерению. Но поскольку повторение этих лекций не планируется, а вместо этого мне сказали, что неплохо было бы дать введение в квантовую механику, то это вы и обнаружите в конце настоящего курса.
Совершенно ясно, что студентам, желающим хорошо разобраться в физике, можно было бы подождать с изучением квантовой механики и до третьего курса. Но, возражая, мне выдвинули довод, что многие студенты с моего курса изучают физику только в качестве основы для занятий другими науками. Обычный же способ изучения квантовой механики делает ее почти недоступной для большинства студентов, потому что у них нет возможности так долго изучать ее. А в то же время вся махина дифференциальных уравнений, весь такой подход к квантовой механике редко используется в ее применениях, в частности в таких более сложных применениях, как электроника и химия. Поэтому я попробовал описать принципы квантовой механики так, чтобы знания уравнений в частных производных вначале не требовалось. Даже физику, я думаю, будет интересно такое изложение квантовой механики (по причинам, которые станут ясны из самих лекций). И все же мне кажется, что эксперимент с квантовой механикой не очень удался главным образом из–за того, что мне не хватило времени и конец пришлось скомкать (мне бы нужно было еще 3–4 лекции, чтобы полней изложить такие вопросы, как энергетические полосы и пространственная зависимость амплитуд). Да и, кроме того, я никогда прежде не излагал материал таким способом и отсутствие обратной связи ощущал особенно остро. Теперь я думаю, что квантовую механику надо излагать все–таки позже. Не исключено, что у меня появится возможность еще раз прочесть этот курс. Тогда я сделаю это получше.
В этом курсе нет лекций, посвященных решению задач. Они решались на семинарах. Хотя на трех лекциях я решал задачи, но в курс они не вошли. После лекции о вращающихся системах была прочитана лекция об инерциальной навигации, но, к сожалению, при издании ее опустили. Пятую и шестую лекции прочитал Мэтью Сэндс (я уезжал тогда из города).
Возникает естественный вопрос, насколько этот эксперимент удался. Моя личная точка зрения, которую, впрочем, не разделяют работавшие со студентами преподаватели, довольно пессимистична. Мне не кажется, что я хорошо поступил со студентами. Когда я наблюдал, как большинство студентов решает задачки на экзаменах, я подумывал о крахе всей моей системы преподавания. Правда, мои друзья напомнили мне, что среди студентов оказался десяток–другой разобравшихся, как это ни странно, почти во всем, активно трудившихся над материалом и подолгу с увлечением мучившихся над трудными вопросами. Эти ребята, на мой взгляд, обладают сейчас первоклассной подготовкой по физике, и я попытаюсь после всего заполучить их к себе на работу. Впрочем, «обучение редко приносит плоды кому–либо, кроме тех, кто предрасположен к нему, но им оно почти не нужно» (Гиббоне).
Тем не менее я не хотел бы бросать ни одного студента на произвол судьбы, как это, видимо, бывало при чтении курса. Как все–таки помочь студентам? Может быть, надо больше поработать над составлением комплекса задач, которые могли бы пролить свет на идеи, развиваемые в лекциях? Задачи дадут хорошую возможность расширить лекционный материал и помогут сделать идеи лекций более осязаемыми и полными, лучше уложить их в голове.
Все же я думаю, что самое лучшее решение проблемы образования – это понять, что самым превосходным обучением является прямая, личная связь между учеником и хорошим учителем, когда ученик обсуждает идеи, размышляет о разных вещах и беседует о них. Невозможно многому научиться, просто отсиживая лекции или даже просто решая задачи. Но в наше время такое множество студентов должно быть обучено, что для идеалов приходится подыскивать эрзацы. Может быть, мои лекции помогут в этом. Может быть, в тех краях, где можно найти отдельного учителя для каждого ученика, эти лекции смогут вдохновить учителя и подбросить ему кое–какие идеи. Может быть, поразмыслив над ними, он только позабавится, а может, и разовьет их дальше.
Июнь 1963
Предисловие
В основу этой книги легли лекции по общей физике, которые профессор Р. Фейнман читал в 1961–1962 академическом году в Калифорнийском Технологическом институте. Это – первая половина двухгодичного вводного курса, обязательного для всех студентов КАЛТЕХа. В 1962–1963 академическом году был прочитан второй цикл лекций, чем завершилась основная часть рассчитанной на четыре года работы по перестройке вводного курса физики.
Необходимость такого коренного пересмотра курса вызывалась не только быстрым развитием физики за последние десятилетия, но и тем, что в последние годы первокурсники приходили в КАЛТЕХ с более глубокой математической подготовкой, чем раньше, – результат улучшения преподавания математики в средней школе. Мы хотели, используя преимущества более прочного математического фундамента, изложить побольше современного материала, что сделало бы курс более интересным, наводящим на размышления и лучше отражающим физику наших дней.
Чтобы иметь представление о том, что надо включить в курс и как это сделать, преподавателям физического факультета было предложено высказать свои идеи в виде краткой программы курса. Возникло несколько проектов перестройки, которые были обсуждены подробно и с пристрастием. Почти все сошлись в одном: перестройку курса нельзя начинать ни просто с переделки уже существующих учебников, ни даже с создания нового учебника; новый курс должен строиться на основе лекций, лекции должны читаться два или три раза в неделю. Создание соответствующих печатных руководств – это будет уже следующий шаг; эти же лекции определят и содержание будущих лабораторных работ. Вчерне были обрисованы общие контуры курса, но это был лишь предварительный набросок, многое в нем выглядело спорным и могло измениться по усмотрению того, кто взялся бы за чтение лекций.
Обсуждались и многочисленные варианты осуществления проекта. Первоначально предполагалось, что будет создана группа из N основных участников (лекторов), которые поровну распределят работу: каждый возьмет себе 1/
Счастливая идея о том, как все же можно создать, быть может, не просто новый курс, отличный от других, а, возможно, уникальный, пришла профессору Сэндсу. Он предложил, чтобы профессор Р. Фейнман подготовил и прочел лекции, которые будут записаны на магнитофонную ленту. После обработки и издания этих лекций получился бы новый учебник. Вот суть принятого в конце концов плана.
Сначала ожидалось, что необходимая редакторская работа сведется к подбору рисунков, расстановке запятых и исправлению грамматических ошибок; этим могли бы заняться между делом один–два студента старших курсов. К несчастью, эти надежды жили недолго. Оказалось, что даже простое приведение записей лекций к пригодному для чтения виду, даже без переработки и пересмотра материала лекций, требует много времени. Такая работа не под силу техническому редактору или студенту, она требует пристального внимания физика–профессионала, причем над каждой лекцией он должен потрудиться часов десять–двадцать.
Трудность редакторской работы, а также необходимость как можно скорее передать лекции в руки студентов сильно затруднили окончательную «доводку» материала, и мы были вынуждены ограничиться созданием предварительного, но годного для издания варианта лекций, который можно было использовать немедленно, хотя и нельзя считать окончательным. Крайняя нужда в большом количестве экземпляров лекций для наших студентов, а также интерес к лекциям студентов и преподавателей других институтов заставили нас издать лекции в их предварительном виде, не дожидаясь окончательной редакции, которой, может быть, никогда и не будет. Мы нисколько не заблуждаемся относительно полноты, связности и логической стройности материала; более того, уже в ближайшем будущем мы собираемся вновь модернизировать курс и думаем, что ни форма, ни содержание его не останутся долго без изменений.
Кроме лекций – наиболее важной части курса, – нужно было позаботиться о задачах, развивающих опыт и умение студентов, и о лабораторных работах, чтобы студенты могли «потрогать руками» изложенный в лекциях материал. Ни то, ни другое еще не достигло той законченности, которую имел материал лекций, хотя кое–что в этом направлении, конечно, сделано. Некоторые задачи были придуманы в ходе чтения лекций, они затем были улучшены, а число их увеличено при повторном чтении курса. Однако мы еще не уверены в том, что эти задачи достаточно разнообразны и углубляют содержание лекций настолько, чтобы студенты могли сами полностью понять, каким мощным аппаратом они владеют. Поэтому задачи будут опубликованы отдельно и в таком виде, который бы допускал их более или менее частую переделку.
Профессор Неер предложил включить в курс несколько новых опытов. Среди них опыты, основанные на использовании воздушных подшипников с чрезвычайно малым трением: новый линейный воздушный желоб, с помощью которого можно количественно изучить одномерное движение, соударения тел и гармоническое движение; а также поддерживаемый на воздушной подушке и движимый воздухом максвелловский волчок, с помощью которого можно изучить вращение с ускорением, прецессию и нутацию гироскопа. Разработка новых лабораторных опытов будет, по–видимому, продолжаться в течение значительного времени.
Этот пересмотр учебной программы возглавляли профессора Р. Лейтон, Г. Неер и М. Сэндс. Официально в этой работе принимали участие профессора Р. Фейнман, Г. Нойгебауер, Р. Саттон, Г. Стаблер, Ф. Стронг и Р. Фогт с кафедр физики, математики и астрономии, а также профессора Т. Кофи, М. Плес–сет и К. Уилтс с кафедры технических наук. Мы сердечно благодарим за ценную помощь всех тех, кто принимал участие в пересмотре курса. Особенно мы обязаны фонду Форда, без финансовой помощи которого эта работа никогда не была бы осуществлена.
Июль 1963
Глава 1 АТОМЫ В ДВИЖЕНИИ
§ 1. Введение
Этот двухгодичный курс физики рассчитан на то, что вы, читатель, собираетесь стать физиком. Положим, это не так уж обязательно, но какой преподаватель не надеется на это! Если вы и впрямь хотите быть физиком, вам придется много поработать. Как–никак, а двести лет бурного развития самой мощной области знания что–нибудь да значат! Такое обилие материала, пожалуй, и не усвоишь за четыре года; вслед за этим нужно еще прослушать специальные курсы.
И все же весь результат колоссальной работы, проделанной за эти столетия, удается сконденсировать – свести в небольшое число
Вы спросите: почему бы сразу, на первой же странице, не привести основные законы, а после только показывать, как они работают в разных условиях? Ведь именно так поступают в геометрии: сформулируют аксиомы, а потом остается только делать выводы. (Неплохая мысль: изложить за 4 минуты то, что и в 4 года не уложишь.) Сделать это невозможно по двум причинам. Во–первых, нам известны
Каждый шаг в изучении природы – это всегда только
Принцип науки, почти что ее определение, состоит в следующем:
Мы сказали, что законы природы – это приближения; сперва открывают «неправильные» законы, а потом уж – «правильные». Но как опыт может быть «неверным»? Ну, во–первых, по самой простой причине: когда в ваших приборах что–то неладно, а вы этого не замечаете. Но такую ошибку легко уловить, надо лишь все проверять и проверять. Ну, а если не придираться к мелочам,
Но самое замечательное, что
Так что же нам нужно изучить сначала? Учить ли нам
Давайте перейдем к нашей схеме, к очерку нашего понимания современной науки (в первую очередь физики, но также и прочих близких к ней наук), так что, когда позже нам придется вникать в разные вопросы, мы сможем видеть, что лежит в их основе, чем они интересны и как укладываются в общую структуру.
Итак,
§ 2. Вещество состоит из атомов
Если бы в результате какой–то мировой катастрофы все накопленные научные знания оказались бы уничтоженными и к грядущим поколениям живых существ перешла бы только одна фраза, то какое утверждение, составленное из наименьшего количества слов, принесло бы наибольшую информацию? Я считаю, что это –
Чтобы показать силу идеи атома, представим себе капельку воды размером 0,5
 |
Это капля воды, увеличенная в миллиард раз, но, конечно, картина эта условная. Прежде всего частицы изображены здесь упрощенно, с резкими краями – это первая неточность. Для простоты они расположены на плоскости, на самом же деле они блуждают во всех трех измерениях – это во–вторых. На рисунке видны «кляксы» (или кружочки) двух сортов – черные (кислород) и белые (водород); видно, что к каждому кислороду пристроились два водорода. (Такая группа из атома кислорода и двух атомов водорода называется молекулой.) Наконец, третье упрощение заключается в том, что настоящие частицы в природе беспрерывно дрожат и подпрыгивают, крутясь и вертясь одна вокруг другой. Вы должны представить себе на картинке не покой, а движение. На рисунке нельзя также показать, как частицы «липнут друг к другу», притягиваются, пристают одна к одной и т. д. Можно сказать, что целые их группы чем–то «склеены». Однако ни одно из телец не способно протиснуться сквозь другое. Если вы попробуете насильно прижать одно к другому, они оттолкнутся.
Радиус атомов примерно равен 1 или 2 на 10–8
Представьте теперь себе эту каплю воды с ее частичками, которые приплясывают, играют в пятнашки и льнут одна к другой. Вода сохраняет свой объем и не распадается на части именно из–за взаимного притяжения молекул. Даже катясь по стеклу, капля не растекается, опять–таки из–за притяжения. И все вещества не улетучиваются по той же причине. Движение частиц в теле мы воспринимаем как
На фиг. 1.2 показан пар.
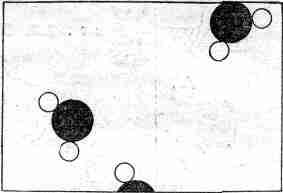 |
Фиг. 1.2. Пар под микроскопом.
Рисунок этот плох в одном – при выбранном нами увеличении на комнату придется всего несколько молекул, поэтому сомнительно, чтобы целых 21/2 молекулы оказались на таком маленьком рисунке. На такой площадке скорее всего не окажется ни одной частицы. Но ведь надо что–то нарисовать, чтоб рисунок не был совсем пустым. Глядя на пар, легче увидеть характерные черты молекул воды. Для простоты на рисунке угол между атомами водорода взят 120°. На самом же деле он равен 105°3', а промежуток между центрами атомов кислорода и водорода равен 0,957 ?. Как видите, мы довольно хорошо представляем себе эту молекулу.
Давайте рассмотрим некоторые свойства водяного пара или других газов. Разрозненные молекулы пара то и дело ударяются о стенки сосуда. Представьте себе комнату, в которой множество теннисных мячей (порядка сотни) беспорядочно и беспрерывно прыгают повсюду. Под градом ударов стенки расходятся (так что их надо придерживать). Эту неумолкаемую дробь ударов атомов наши грубые органы чувств (их–то чувствительность не возросла в миллиард раз) воспринимают как
 |
Молекулы для простоты изображены теннисными мячиками, или точечками, потому что форма их не имеет значения. Они движутся беспорядочно и непрерывно. Множество молекул беспрерывно колотит о поршень. Их непрекращаемые удары вытолкнут его из цилиндра, если не приложить к поршню некоторую силу –
А если в сосуде число молекул удвоится (и соответственно возрастет их плотность), а скорости их (и соответственно температура) останутся прежними? Тогда довольно точно удвоится и число ударов, а так как каждый из них столь же «энергичен», как и раньше, то выйдет, что давление пропорционально плотности. Если принять во внимание истинный характер сил взаимодействия атомов, то следует ожидать и небольшого спада давления из–за увеличения притяжения между атомами и легкого роста давления из–за увеличения доли общего объема, занятого самими атомами. И все же в хорошем приближении, когда атомов сравнительно немного (т. е. при невысоких давлениях),
Легко понять и нечто другое. Если повысить температуру газа (скорость атомов), не меняя его плотности, что произойдет с давлением? Двигаясь быстрей, атомы начнут бить по поршню сильней; к тому же удары посыплются чаще – и давление возрастет. Вы видите, до чего просты идеи атомной теории.
А теперь рассмотрим другое явление. Пускай поршень медленно двинулся вперед, заставляя атомы тесниться в меньшем объеме. Что бывает, когда атом ударяет по ползущему поршню? Ясно, что после удара его скорость повышается. Можете это проверить, играя в пинг–понг: после удара ракеткой шарик отлетает от ракетки быстрей, чем подлетал к ней. (Частный пример: неподвижный атом после удара поршня приобретает скорость.) Стало быть, атомы, отлетев от поршня, становятся «горячее», чем были до толчка. Поэтому все атомы в сосуде наберут скорость. Это означает, что
Вернемся к нашей капельке воды и посмотрим, что с ней будет, когда температура понизится. Положим, что толчея среди молекул воды постепенно утихает. Меж ними, как мы знаем, существуют силы притяжения; притянувшимся друг к другу молекулам уже нелегко покачиваться и прыгать. На фиг. 1.4 показано, что бывает при низких температурах; мы видим уже нечто новое. Образовался
Таким образом, лед имеет
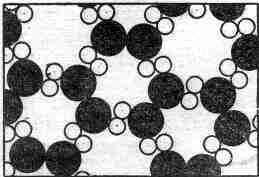 |
Смотрите, как много «пустот» на рисунке; у настоящего льда их тоже много. Когда система разрушается, все эти пустоты заполняются молекулами. Большинство простых веществ, за исключением льда и гарта (типографского сплава), при плавлении
Но хотя лед обладает «жесткой» кристаллической структурой, его температура может тоже меняться, в нем есть запас тепла. Этот запас можно менять по своему желанию. Что же это за тепло? Атомы льда все равно не находятся в покое. Они дрожат и колеблются. Даже когда существует определенный порядок в кристалле (структура), все атомы все же колеблются «на одном месте». С повышением температуры размах их колебаний все растет, пока они не стронутся с места. Это называется
Этого минимального количества движения не хватает, чтобы растопить тело. Но есть одно исключение – гелий. Гелий при охлаждении тоже уменьшает движение своих атомов до предела, но даже при абсолютном нуле в них оказывается достаточный запас движения, чтобы предохранить гелий от замерзания. Гелий не замерзает и при абсолютном нуле, если только не сжимать его под высоким давлением. Повышая давление,
§ 3. Атомные процессы
Так с атомной точки зрения описываются твердые, жидкие и газообразные тела. Но атомная гипотеза описывает и
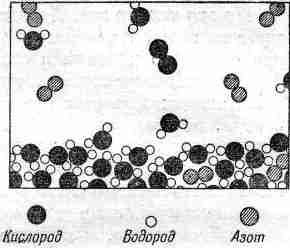 |
Мы по–прежнему видим молекулы, образующие толщу воды, но, кроме того, здесь изображена и ее поверхность, а над нею – различные молекулы: прежде всего молекулы воды в виде
Итак, над поверхностью воды находится воздух – газ, содержащий некоторое количество водяного пара. Что происходит на этом рисунке? Молекулы воды все время движутся. Время от времени какая–нибудь из молекул близ поверхности получает толчок сильнее остальных и выскакивает вверх. На рисунке этого, конечно, не видно, потому что здесь все
Почему же мы
Но это еще не все. Давайте подумаем, какие молекулы вылетают из воды? Если уж молекула выскочила, то это значит, что она случайно вобрала в себя излишек энергии; он ей понадобился, чтобы разорвать путы притяжения соседей. Энергия вылетающих молекул превосходит среднюю энергию молекул в воде, поэтому энергия остающихся молекул
Вы понимаете, конечно, что на самом деле все происходит гораздо сложнее, чем здесь описано. Не только вода переходит в воздух, но молекулы кислорода или азота время от времени переходят в воду и «теряются» в массе молекул воды. Попадание атомов кислорода и азота в воду означает растворение воздуха в воде; если внезапно из сосуда воздух выкачать, то молекулы воздуха начнут из воды выделяться быстрее, чем проникают в нее; мы увидим, как наверх подымаются пузырьки. Вы, наверно, слыхали, что это явление очень вредно для ныряльщиков.
Перейдем теперь к другому процессу. На фиг. 1.6 мы видим, как (с атомной точки зрения) соль растворяется в воде.
 |
Что получается, если в воду бросить кристаллик соли? Соль – твердое тело, кристалл, в котором «атомы соли» расставлены правильными рядами. На фиг. 1.7 показано трехмерное строение обычной соли (хлористого натрия).
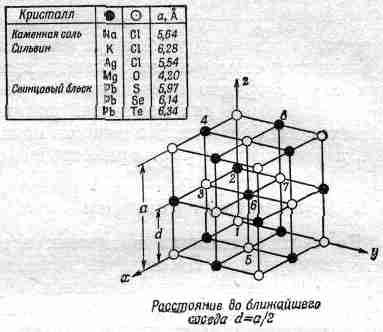 |
Строго говоря, кристалл состоит не из атомов, а из
Вернемся к вопросу о растворении и осаждении соли. Если повысить температуру раствора соли, то возрастет и число растворяющихся атомов и число осаждаемых. Оказывается, что в общем случае трудно предсказать, в какую сторону сдвинется процесс, быстрей или медленней пойдет растворение. С ростом температуры большинство веществ начинает растворяться сильней, а у некоторых растворимость падает.
§ 4. Химические реакции
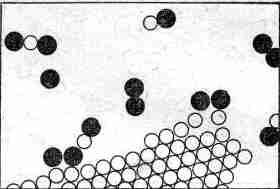 |
Процесс, в котором атомные партнеры меняются местами, называется
Предположим, что атомы углерода образуют твердый кристалл (графит или алмаз). Одна из молекул кислорода может пробраться к углероду, каждый ее атом подхватит по атому углерода и улетит в новом сочетании углерод – кислород. Такие молекулы образуют газ, называемый угарным. Его химическое имя СО. Что это значит? Буквы СО – это фактически картинка такой молекулы: С – углерод, О – кислород. Но углерод притягивает к себе кислород намного сильнее, чем кислород притягивает кислород или углерод – углерод. Поэтому кислород для этого процесса может поступать с малой энергией, но, схватываясь с неимоверной жадностью и страстью с углеродом, высвобождает энергию, поглощаемую всеми соседними атомами. Образуется большое количество энергии движения (кинетической энергии). Это, конечно, и есть
Вдобавок молекулы СО могут не удовольствоваться достигнутым. У них есть возможность подсоединить еще один атом кислорода; возникает более сложная реакция: кислород в паре с углеродом столкнется с другой молекулой СО. Атом кислорода присоединится к СО и в конечном счете образуется молекула из одного углерода и двух кислородов. Ее обозначают С02 и называют углекислым газом. Когда углерод сжигают очень быстро (скажем, в моторе автомашины, где взрывы столь часты, что углекислота не успевает образоваться), то возникает много угарного газа. Во многих таких перестановках атомов выделяется огромное количество энергии, наблюдаются взрывы, вспыхивает пламя и т. д.; все зависит от реакции.
Химики изучили эти расположения атомов и установили, что любое вещество – это свой тип
Чтобы объяснить эту мысль, рассмотрим новый пример. У клумбы фиалок вы сразу чувствуете их «запах». Это значит, что в ваш нос попали
И вот химики могут взять даже такие необычные молекулы, как молекулы запаха фиалок, проанализировать их строение и описать нам
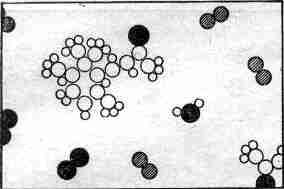 |
Снова мы находим здесь азот, кислород, водяной пар… (А он–то откуда здесь? От
Среди них, однако, витает «чудовище», сложенное из атомов углерода, водорода и кислорода, облюбовавших для себя особого вида расположение. Это расположение намного сложнее, чем у углекислоты. К сожалению, мы не можем его нарисовать: хотя оно известно химикам очень точно, но оно ведь трехмерное, а как его изобразишь в двух измерениях?! Как нарисовать шесть углеродов, которые образуют кольцо, но не плоское, а «гармошкой»? Все углы, все расстояния в ней известны. Так вот, химическая
Как же химик узнает, что это за расположение? Возьмет он две пробирки с веществом, сольет их содержимое и смотрит: если смесь покраснела, значит, к такому–то месту молекулы прикреплен один водород и два углерода; если посинела, то… то это ничего не значит. Органическая химия может поспорить с самыми фантастическими страницами детективных романов. Чтобы узнать, как расположены атомы в какой–нибудь невероятно сложной молекуле, химик смотрит, что будет, если смешать два разных вещества! Да физик нипочем не поверит, что химик, описывая расположение атомов, понимает, о чем говорит. Но вот уже больше 20 лет, как появился физический метод, который позволяет разглядывать молекулы (не такие сложные, но по крайней мере родственные) и описывать расположение атомов не по цвету раствора, а по
Оказывается, что действительно в запахе фиалок присутствуют три слегка различные молекулы, они отличаются только расстановкой атомов водорода.
Одна из проблем в химии – это придумать такое название для вещества, чтобы по нему можно было бы узнать, какое оно. Найти имя для его формы! Но оно должно описывать не только форму, а указывать еще, что здесь стоит кислород, а вон там – водород, чтобы было точно отмечено, где что стоит. Теперь вы понимаете, почему химические названия так сложны. Это не сложность, а полнота. Название молекулы запаха фиалок поэтому таково: 4-(2,2,3,6–тетраметил–5–циклогексан)-3–бутен–2–он. Оно полностью описывает строение молекулы (изображенной на фиг. 1.10), а его длина объясняется сложностью молекулы.
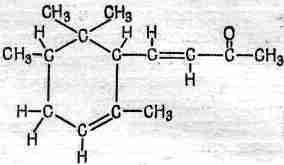 |
Дело, значит, вовсе не в том, что химики хотят затуманить мозги, просто им приходится решать сложнейшую задачу описания молекулы словами!
Но откуда мы все–таки
Другие доказательства существования атомов можно извлечь из строения кристаллов. Во многих случаях их строение, определенное из опытов по прохождению рентгеновских лучей через кристаллы, согласуется по своему пространственному расположению с формой самого природного кристалла. Углы между разными гранями кристалла согласуются с точностью не до градусов, а до секунд дуги с углами, высчитанными в предположении, что кристалл сложен из множества «слоев» атомов.
Да посудите сами! Если уж стальной кубик или кристаллик соли, сложенный из одинаковых рядов одинаковых атомов, может обнаруживать такие интересные свойства; если вода – простые капельки, неотличимые друг от друга и покрывающие миля за милей поверхность Земли, – способна порождать волны и пену, гром прибоя и странные узоры на граните набережной; если все это, все богатство жизни вод – всего лишь свойства сгустков атомов, то
*
Глава 2 ОСНОВНЫЕ ФИЗИЧЕСКИЕ ВОЗЗРЕНИЯ
§ 1. Введение
В этой главе будут рассмотрены самые основные представления о физике; здесь будет идти речь о том, как теперь мы представляем себе природу вещей. Я не буду рассказывать историю того, как стало известно, что эти представления правильны; это мы отложим до другого раза.
Предмет науки предстает перед нами во множестве проявлений, в обилии признаков. Спуститесь к морю, вглядитесь в него. Это ведь не просто вода. Это вода и пена, это рябь и набегающие волны, это облака, солнце и голубое небо, это свет и тепло, шум и дыхание ветра, это песок и скалы, водоросли и рыба, их жизнь и гибель, это и вы сами, ваши глаза и мысли, ваше ощущение счастья. И не то ли в любом другом месте, не такое ли разнообразие явлений и влияний? Вы не найдете в природе ничего простого, все в ней перепутано и слито. А наша любознательность требует найти в этом простоту, требует, чтобы мы ставили вопросы, пытались ухватить суть вещей и понять их многоликость как возможный итог действия сравнительно небольшого количества простейших процессов и сил, на все лады сочетающихся между собой.
И мы спрашиваем себя: отличается ли песок от камня? Быть может, это всего лишь множество камешков? А может, и Луна – огромный камень? Тогда, поняв что такое камни, не поймем ли мы тем самым природу песка и Луны? А ветер – что это такое? Может, это всплески воздуха, как вон те всплески воды у берега? Что общего между всяким движением? А есть ли что–нибудь общее между всевозможными звуками? Сколько получится, если пересчитать все цвета? И так далее и так далее. Вот так мы постепенно пробуем проанализировать все вокруг, связать то, что кажется несвязуемым, в надежде, что удастся
Способ получать частичные ответы на подобные вопросы был придуман еще несколько сот лет назад.
Что значит «понять» что–либо? Представьте себе, что сложный строй движущихся объектов, который и есть мир, – это что–то вроде гигантских шахмат, в которые играют боги, а мы следим за их игрой. В чем правила игры, мы не знаем; все, что нам разрешили, – это
Но откуда мы знаем, что те правила, которые мы «ощущаем», справедливы на самом деле? Ведь мы не способны толково разобрать ход игры. Существует, грубо говоря, три способа проверки. Во–первых, мыслимы положения, когда природа устроена (или мы ее устраиваем) весьма просто, всего из нескольких частей; тогда можно точно предсказать все, что случится, проверив тем самым правила. (В углу доски может оказаться всего несколько фигур, и все их движения легко себе представить.)
Есть и второй довольно неплохой путь проверки правил: надо из этих правил вывести новые, более общие. Скажем, слон ходит только по диагонали; значит, сколько бы он ни ходил, он всегда окажется, например, на черном поле. Стало быть, не вникая в детали, наши представления о движении слона всегда можно проверить по тому, остается ли он все время на черном поле. Конечно, не исключено, что внезапно слон очутится на
Есть и третий способ убедиться, что наши представления об игре правильны; мало оправданный по существу, он, пожалуй, самый мощный из всех способов. Это путь
Когда–то все явления природы грубо делили на классы – теплота, электричество, механика, магнетизм, свойства веществ, химические явления, свет (или оптика), рентгеновские лучи, ядерная физика, тяготение, мезонные явления и т. д. Цель–то, однако, в том, чтобы понять
Вот взятые из истории примеры слияния. Во–первых,
Возникает естественный вопрос: будет ли возможно в конце концов
§ 2. Физика до 1920 года
Нам было бы нелегко начать прямо с сегодняшних взглядов. Посмотрим лучше, как выглядел мир примерно в 1920 г., а затем сотрем с этой картины лишнее.
До 1920 г. картина была примерно такова. «Сцена», на которой выступает Вселенная, – это трехмерное
Продолжаем наше описание природы. С этой точки зрения газ, как, впрочем, и
Какие
Дальше возникала проблема:
Что же тогда получается? Положим, что два различных сорта (плюс и минус) приложены друг к другу вплотную. Третий заряд находится вдалеке. Почувствует ли он притяжение?
Чтобы дать представление о том, насколько электричество сильнее тяготения, расположим две песчинки размером в миллиметр в 30
Зная все это, легко было представить себе и устройство атома. Считалось, что в центре его положительно заряженное электричеством очень массивное «ядро», оно окружено некоторым числом «электронов», очень легких и заряженных отрицательно. Забегая вперед, заметим, что впоследствии в самом ядре были обнаружены два рода частиц – протоны и нейтроны, весьма тяжелые и обладающие близкими массами. Протоны заряжены положительно, а нейтроны не заряжены вовсе. Когда в ядре атома имеется шесть протонов и ядро окружено шестью электронами (отрицательные частицы обычного мира материальных тел – все электроны, они намного легче протонов и нейтронов), то этот атом в химической таблице стоит под номером 6 и называется углеродом. Атом, имеющий номер 8, называется кислородом, и т. д. Химические свойства зависят от внешней
И еще многое другое стало известно об электрической силе. Естественно было бы толковать электрическое взаимодействие как простое притяжение двух предметов, положительно и отрицательно заряженных. Однако выяснилось, что такой подход плохо помогает уяснению природы электрической силы. Толкование, более отвечающее положению вещей, таково: когда где–то имеется положительный заряд, то он искривляет в каком–то смысле пространство, создает в нем некоторое условие для того, чтобы минус–заряд, помещенный в это пространство, ощутил действие силы. Эта возможность порождать силы называется
Что–то похожее на это происходит, если в бассейн с водой брошен поплавок; можно подействовать на него «непосредственно», бросив в воду поблизости другой поплавок; при этом если вы смотрели
Электромагнитное поле может передавать волны; одни волны – это
 |
И наконец, неслыханно высокие частоты (в тысячу раз больше) обнаруживаются далее в волнах, присутствующих в
§ 3. Квантовая физика
Мы описали электромагнитное поле и поняли, что оно может передаваться как волны. Сейчас мы увидим, что на самом деле эти волны ведут себя очень странно: они отнюдь не похожи на волны. На высоких частотах они гораздо больше смахивают на
А затем также выяснилось, что и законы движения частиц неверны. Механические законы «инерции» и «силы», законы Ньютона – все они оказались
Много особенностей есть у квантовой механики. В первую очередь она запрещает считать, что частица может двигаться через определенное точно указанное место с определенной точно указанной скоростью. Чтоб показать, насколько ошибочна обычная механика, отметим, что в квантовой механике имеется правило, согласно которому никто в одно и то же время не может знать и место и быстроту движения частицы. Неопределенность в импульсе и неопределенность в положении частицы дополняют друг друга: их произведение постоянно. Мы пока напишем это правило в виде ?x?p?h/2?, не вникая в подробности. Это правило представляет собой объяснение таинственного парадокса: раз атомы сделаны из плюс–и минус–зарядов, отчего бы минус–зарядам просто не усесться на плюс–заряды (они ведь притягиваются), отчего бы им не сблизиться до того тесно, что они погасят друг друга?
А вот другое интереснейшее изменение в идеях и философии науки, осуществленное квантовой механикой: невозможно никогда предсказать
Кстати, философы порой много говорят о вещах,
Вернемся опять к квантовой механике и к основам физики. Мы не будем пока входить в детали квантовомеханических принципов, их не так просто понять. Мы их просто примем, как они есть, а остановимся на кое–каких их следствиях. Вот одно из них: то, что мы обычно считаем волнами, может вести себя как частица; частицы же ведут себя как волны; то же относится и к любым телам. Между волной и частицей просто нет различия. Квантовая механика
Возникает к тому же и новый взгляд на электромагнитное взаимодействие. В добавление к электрону, протону и нейтрону появляется новая
Далее, квантовая электродинамика – в принципе это также теория всей химии и всех жизненных процессов, если предположить, что жизнь сводится в конечном счете к химии, а значит, и к физике (сама химия уже свелась к физике, и та часть физики, которая включает в себя химию, уже разработана). Мало того, та же квантовая электродинамика, эта величественная наука, предсказывает немало и новых явлений. Во–первых, она говорит о свойствах фотонов очень высоких энергий, гамма–излучения и т. д. Она предсказала еще одно очень оригинальное явление, а именно, что, кроме электрона, должна существовать другая частица с той же массой, но с противоположным зарядом, так называемый
По–видимому, справедливо и обобщение этого правила: существование античастицы для любой частицы. Античастица электрона носит имя позитрона; у других частиц названия присвоены по другому принципу: если частицу назвали
§4. Ядра и частицы
Из чего состоят ядра? Чем части ядра удерживаются вместе? Обнаружено, что существуют силы огромной величины, которые и удерживают составные части ядра. Когда эти силы высвобождаются, то выделяемая энергия по сравнению с химической энергией огромна, это все равно, что сравнить взрыв атомной бомбы со взрывом тротила. Объясняется это тем, что атомный взрыв вызван изменениями внутри ядра, тогда как при взрыве тротила перестраиваются лишь электроны на внешней оболочке атома.
Так каковы же те силы, которыми нейтроны и протоны скреплены в ядре?
Электрическое взаимодействие связывают с частицей – фотоном. Аналогично этому Юкава предположил, что силы притяжения между протоном и нейтроном обладают полем особого рода, а колебания этого поля ведут себя как частицы. Значит, не исключено, что, помимо нейтронов и протонов, в мире существуют некоторые иные частицы. Юкава сумел вывести свойства этих частиц из уже известных характеристик ядерных сил. Например, он предсказал, что они должны иметь массу, в 200– 300 раз большую, чем электрон. И– о, чудо! – в космических лучах как раз открыли частицу с такой массой! Впрочем, чуть погодя выяснилось, что это совсем не та частица. Назвали ее ? — мезон, или мюон.
И все же несколько попозже, в 1947 или 1948г., обнаружилась частица – ? — мезон, или пион, – удовлетворявшая требованиям Юкавы. Выходит, чтобы получить ядерные силы, к протону и нейтрону надо добавить пион. «Прекрасно! – воскликнете вы. – С помощью этой теории мы теперь соорудим квантовую ядродинамику, и пионы послужат тем целям, ради которых их ввел Юкава; посмотрим, заработает ли эта теория, и если да, то объясним все». Напрасные надежды! Выяснилось, что расчеты в этой теории столь сложны, что никому еще не удалось их проделать и извлечь из теории какие–либо следствия, никому не выпала удача сравнить ее с экспериментом. И тянется это уже почти 20 лет!
С теорией что–то не клеится; мы не знаем, верна она или нет; впрочем, мы уже знаем, что в ней чего–то не достает, что
Но химических элементов ведь тоже было множество, и внезапно между ними удалось увидеть связь, выраженную периодической таблицей Менделеева. Скажем, калий и натрий – вещества, близкие по химическим свойствам, – в таблице попали в один столбец. Так вот, попробовали соорудить таблицу типа таблицы Менделеева и для новых частиц. Одна подобная таблица была предложена независимо Гелл–Манном в США и Нишиджимой в Японии. Основа их классификации – новое число, наподобие электрического заряда. Оно присваивается каждой частице и называется ее «странностью»
В табл. 2.2 приведены новые частицы. Мы не будем пока подробно говорить о них. Но из таблицы по крайней мере видно, как мало мы еще знаем. Под символом каждой частицы стоит ее масса, выраженная в определенных единицах, называемых мегаэлектронвольт, или
Частицы подчеркнуты сплошной линией, «резонансы» – штрихами. Некоторых частиц в таблице нет совсем: нет фотона и гравитона, очень важных частиц с нулевыми массой и зарядом (они не попадают в барион–мезон–лептонную схему классификации), нет и кое–каких новейших резонансов (?,
 |
Частицы, стоящие вместе с нейтроном и протоном, называют
Для ядерных взаимодействий, кроме барионов, необходимы другие частицы –
Подобно тому как из очень удачной таблицы Менделеева выпали некоторые редкие земли, точно так же из нашей таблицы выпадают некоторые частицы. Это те частицы, которые с ядрами сильно не взаимодействуют, к ядерному взаимодействию отношения не имеют и между собой сильно тоже не взаимодействуют (под сильным понимается мощный тип взаимодействия, дающего атомную энергию). Называются эти частицы
И наконец, существуют еще две частицы, тоже с ядрами не взаимодействующие. Одну мы знаем уже – это фотон; а если поле тяготения также обладает квантовомеханическими свойствами (хотя пока квантовая теория тяготения не разработана), то, возможно, существует и частица гравитон с массой нуль.
Что такое «масса нуль»? Массы, которые мы приводили, это массы
Итак, мы встретились с целым строем частиц, которые все вместе, по–видимому, являются очень фундаментальной частью вещества. К счастью, эти частицы
 |
Положение, в котором находится современная физика, следует считать ужасным. Я бы подытожил его такими словами: вне ядра мы, видимо, знаем все; внутри него справедлива квантовая механика, нарушений ее принципов там не найдено.
Сцена, на которой действуют все наши знания, – это релятивистское пространство–время; не исключено, что с ним связано и тяготение. Мы не знаем, как началась Вселенная, и мы ни разу не ставили опытов с целью точной проверки наших представлений о пространстве–времени на малых расстояниях, мы только
Глава 3 ФИЗИКА И ДРУГИЕ НАУКИ
§ 1. Введение
Физика – это самая фундаментальная из всех наук, самая всеобъемлющая; огромным было ее влияние на все развитие науки. Действительно, ведь нынешняя физика вполне равноценна давнишней
В этой главе мы попытаемся рассказать, какого рода фундаментальные проблемы встают перед соседними науками. Жаль, что нам не придется по–настоящему заняться этими науками, их проблемами; мы не сможем прочувствовать всю их сложность, тонкость и красоту. Из–за нехватки места мы не коснемся также связи физики с техникой, с промышленностью, с общественной жизнью и военным искусством. Даже на замечательной связи, объединяющей физику с математикой, мы не задержимся. (Математика, с нашей точки зрения, не наука в том смысле, что она не относится к
§ 2. Химия
Химия испытывает на себе влияние физики, пожалуй, сильней, чем любая другая наука. Когда–то, в свои младенческие годы, когда химия почти целиком сводилась к тому, что мы сейчас называем неорганической химией (т. е. химии веществ, не связанных с живыми телами), когда кропотливым трудом химиков открывались многие химические элементы, их связь друг с другом, изучались их соединения, анализировался состав почвы и минералов, в те годы химия сыграла важную роль в становлении физики. Эти науки взаимодействовали очень сильно: вся теория атомного строения вещества получила основательную поддержку в химическом эксперименте. Химическую теорию, т. е. теорию самих реакций, подытожила периодическая система Менделеева. Она выявила немало удивительных связей между разными элементами – стало ясно, что с чем и как соединяется; все эти правила составили неорганическую химию. Сами они в свою очередь были в конечном счете объяснены квантовой механикой. Стало быть, на самом деле теоретическая химия – это физика. Однако объяснение, даваемое квантовой механикой, – это все–таки объяснение
Есть к тому же ветвь физики и химии, и очень важная ветвь, к которой они обе приложили руки. Речь идет о применении статистики к тем случаям, когда действуют законы механики, т. е. о
В наше время неорганическая химия как наука свелась в основном к физической и квантовой химии; первая изучает скорости реакций и прочие их детали (как попадает молекула в молекулу, какая из частей молекулы оторвется первой и т. д.), а вторая помогает понимать происходящее на языке физических законов.
Другая ветвь химии –
§ 3. Биология
Итак, мы пришли к науке, которая занята изучением живого, – к
Когда–то между биологией и физикой существовали интересные отношения: именно биология помогла физике открыть
Если вглядеться в биологию живых организмов, можно заметить множество чисто физических явлений: циркуляцию крови, давление и т. п. Взять, к примеру, нервы. Наступив на острый камешек, мы мгновенно узнаем об этом: что–то нам о том говорит, какая–то информация поднимается вверх по ноге. Как же это происходит? Изучая нервы, биологи пришли к выводу, что это очень нежные трубочки со сложными, очень тонкими стенками. Через эти стенки в клетку поступают ионы; получается нечто вроде конденсатора с положительными ионами' снаружи и отрицательными внутри. У такой мембраны есть замечательное свойство: если в одном месте она «разряжается», т. е. если в каком–то месте ионы пройдут насквозь, так что электрическое напряжение здесь упадет, то соседние ионы почувствуют это электрическое влияние; это так подействует на мембрану в соседнем месте, что она тоже пропустит сквозь себя ионы. В свою очередь это скажется на следующем месте и т. д. Возникнет волна «проницаемости» мембраны; она побежит вдоль нервного волокна, если один конец его «возбудится» острым камнем. Выходит словно длинная цепочка костяшек домино, поставленных торчком; толкнешь крайнюю, она – следующую и т. д. Конечно, больше одного сообщения так не передашь, надо снова поднять все костяшки; и в нервной клетке тоже после этого идут процессы медленного накопления ионов и подготовки нерва к новому импульсу. Так мы узнаём, что мы делаем (или по крайней мере где мы находимся). Электрические явления при прохождении нервного импульса, конечно, можно регистрировать электрическими приборами. Поскольку эти явления
Обратное явление происходит, когда откуда–то из мозга по нерву передается сообщение. Что делается тогда на конце нерва? Нерв там дает разветвления, которые связаны с мышечной структурой; называют их
Биология – настолько широкое поле деятельности, что есть уйма проблем, о которых мы даже не упоминаем; скажем, вопрос о том, как осуществляется зрение (что свет делает внутри глаза) или как работает ухо и т. д, (Как работает
Так вот, все эти вопросы, стоящие перед биологией, на самом деле для биолога отнюдь не главные, отнюдь не они лежат в основе жизни. Если мы их и поймем, нам все равно не понять сущности жизни. Вот вам пример: люди, изучающие нервы, понимают, что их работа очень нужна, ведь животных без нервов не бывает. Но
При этом мы установим, что у всех живых существ есть много общих черт. Самое же общее между ними то, что они состоят из
В клетках живых организмов происходит множество хитро задуманных химических реакций: одно соединение превращается в другое, затем в третье, затем еще и еще. Фиг. 3.1 дает некое представление о гигантских усилиях, предпринятых в изучении биохимии; там сведены воедино наши знания о малой доле того множества цепочек реакций (может быть, примерно 1% общего количества), которые происходят в клетке.
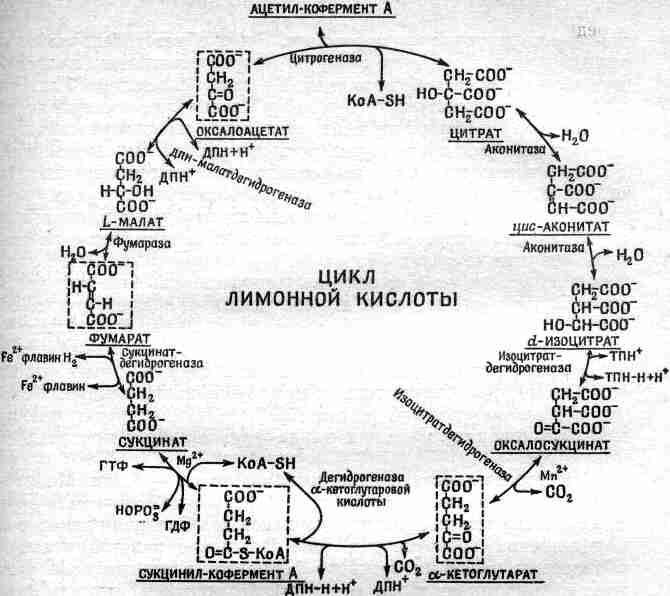 |
Вы видите здесь ряд молекул, последовательно превращающихся одна в другую, – цикл с довольно мелкими шагами. Это – цикл Кребса, или дыхательный цикл. Судя по изменениям в молекулах, каждое вещество и каждый шаг в цикле довольно просты. Но
Сам фермент состоит из другого вещества –
Важнейшая деталь цикла, приведенного на фиг. 3.1, это превращение ГДФ в ГТФ (гуаназиндифосфат в гуаназинтрифосфат), потому что во втором веществе – ГТФ – энергии намного больше, чем в первом. Подобно тому как в некоторых ферментах имеется «ящик» для переноса атомов водорода, бывают еще особые «ящики» для переноса
Есть и другой резон, по которому для биологии и других наук важна именно физика, – это
Вернемся, однако, к описанию ферментов и белков. Не все белки – ферменты, но все ферменты – белки. Существует множество белков, таких, как белки мышц, структурные белки, скажем, в хрящах, волосах, коже, не являющихся ферментами. И все–таки белки – очень характерная для жизни субстанция; во–первых, это составная часть всех ферментов, а во–вторых, составная часть многих иных живых веществ. Структура белков проста и довольно занятна. Они представляют собой ряды, или цепи, различных
Есть и другая проблема в биологии: откуда ферменты «знают», кем им стать? От красноглазой мухи рождается опять красноглазая мушка; значит, вся информация о ферментах, создающих красный пигмент, должна перейти к очередной мушке. Передает эту информацию не белок, а вещество в ядре клетки, ДНК (дезоксирибонуклеиновая кислота). Это – та ключевая субстанция, которая передается от одной клетки к другой (половые клетки, например, почти целиком состоят из ДНК) и уносит с собой инструкцию, как делать ферменты. ДНК – это «калька», печатная матрица. На что похожа эта калька, как она должна действовать? Первое – она должна воспроизводить самое себя; второе – она должна быть способна давать задания белку. Что до первого, то можно было бы думать, что это происходит так же, как воспроизведение клеток: клетки подрастают и делятся пополам. Может быть, молекулы ДНК тоже растут и тоже делятся? Нет, это исключено. Ведь
Структура ДНК долго изучалась сперва химически (составные части), затем рентгенографически (пространственная структура). В результате пришли к следующему знаменательному открытию: молекула ДНК – это пара цепочек, навитых друг на друга. Скелет каждой цепочки, хотя и похожий на белковые цепи, но химически отличный от них, – это ряд сахарных и фосфатных групп, как показано на фиг. 3.2.
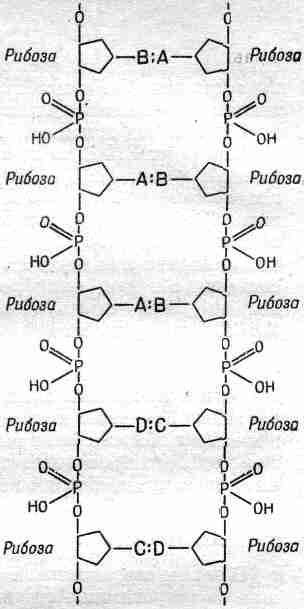 |
Из этой схемы видно, как в цепи может храниться инструкция, ибо, разняв цепочку на две нитки, вы получаете ряд веществ
На схеме видны пары поперечных звеньев, присоединенных к сахарным группам и стягивающих между собой две нити. Эти звенья неодинаковы; есть четыре сорта звеньев – аденин, тимин, цитозин, гуанин, обозначаемые
Как же мыслится при этом воспроизведение? Пусть цепь расщеплена на две. Как сделать другую такую же? Если в веществе клетки есть фабрика, вырабатывающая фосфат, сахар и звенья
Наконец, последний вопрос: как порядок следования
Право же, ни одна наука, ни одна отрасль знаний не движутся так бурно по всем направлениям вперед, как биология. Но если б мы должны были назвать то самое главное, что ведет нас сейчас все вперед и вперед в наших попытках понять явление жизни, мы обязаны были бы сказать:
§ 4. Астрономия
В нашем стремительном обзоре всей Вселенной очередь дошла до астрономии. Астрономия – старше физики. Фактически физика и возникла из нее, когда астрономия заметила поразительную простоту движения звезд и планет; объяснение этой простоты и стало
Каждый атом испускает свет определенных частот, подобно тому как у каждого музыкального инструмента есть свое звучание – определенный набор частот, или высот, звука. Слыша одновременно несколько тонов, мы можем разделить их; но способности нашего глаза в этом отношении далеко не столь велики, он не может разделить смесь цветов на составляющие части. Однако с помощью спектроскопа
Одно из наиболее впечатляющих открытий астрономии – это открытие источника энергии звезд, поддерживающего их горение. Один из тех, кто открыл это, отправился на прогулку с девушкой как раз в ночь после того, как понял, что на звездах происходит
Так вот, Солнце получает энергию от ядерного «сгорания» водорода, который переходит при этом в гелий. Из водорода в глубинах звезд вырабатываются далее другие химические элементы. Вещество, из которого сделаны
§ 5. Геология
Перейдем теперь к так называемым
Главный вопрос геологии заключается в том, что сделало Землю такой, какая она есть? Самые очевидные из таких процессов происходят у нас на глазах: реки подмывают берега, поля заносит пылью и т. д. Это понять довольно легко, но ведь кроме эрозии, помимо разрушения должно что–то и обратное происходить. В среднем горы сейчас не ниже, чем в прошлом. Следовательно, должен происходить и процесс
Изучая геологию, вы убедитесь, что действительно происходит и горообразование, и вулканизм, но никто их не понимает; не понимает того, что составляет половину геологии. Действительно, природа вулканов не понята. Отчего бывают землетрясения, тоже в конечном счете не понято. Понимают, конечно, что если что–то с чем–то столкнется, то что–то треснет, что–то сдвинется – все это хорошо. Но что толкнуло, почему толкнуло? Существует теория, что внутри Земли имеются течения – происходит циркуляция из–за различия температур снаружи и внутри – и они в своем движении слегка толкают поверхность Земли. А если где–то встречаются два противных течения, то там должно накапливаться вещество, появляться горные хребты, они окажутся в сильно напряженном состоянии, возникнут вулканы, произойдут землетрясения.
Что можно сказать о недрах Земли? Хорошо известна скорость волн землетрясений в Земле и распределение плотности внутри нашей планеты. Но физики не смогли создать хорошей теории плотности вещества при давлениях, ожидаемых в центре Земли. Иными словами, мы не представляем себе слишком хорошо свойств вещества в таких условиях. Со своей планетой мы справляемся куда хуже, нежели с состоянием вещества в звездах. Необходимый для этого математический аппарат не разработан, он, по–видимому, чрезвычайно сложен; не исключено, однако, что найдется кто–то, кто поймет важность этой проблемы и разработает ее. Другое дело, что, даже вычислив плотность, мы не сможем представить себе циркулирующие течения или разобраться в свойствах горных пород при сверхвысоких давлениях. Мы не умеем предсказывать, насколько быстро эти породы «поддадутся» давлению; только опыт ответит на эти вопросы.
§ 6. Психология
Рассмотрим, наконец, еще одну науку –
Другие ветви психологии, а в нее входит, например, физиология ощущения (что происходит в глазе, а что в мозге), пожалуй, не столь интересны. Но в них были достигнуты хотя и малые, но вполне реальные успехи. Вот одна из интереснейших технических задач (хотите называйте ее психологией, хотите – нет). Центральная проблема в изучении мышления, или, если угодно, нервной системы, такова: пусть животное чему–либо научилось, пусть оно умеет делать что–то, чего прежде не умело; значит, клетки его мозга, если они состоят из атомов, изменились.
§ 7. С чего все пошло?
Чтобы физика могла быть полезной другим наукам в отношении
Существует и другой
В настоящее время физика не изучает вопросы истории. Мы не задаем вопрос: «Вот законы физики, как они возникли?» Мы не считаем в настоящее время, что законы физики со временем как–то изменяются, что они прежде были иными, нежели ныне. Конечно, это
Наконец, существует физическая проблема, общая многим паукам, очень старая к тому же, но до сего времени не решенная. Это не проблема поиска новых элементарных частиц, нет, это другой вопрос – вопрос давно, свыше ста лет назад, отставленный наукой в сторону. Ни один физик еще не смог математически безупречно проанализировать его, несмотря на его важность для сопредельных наук. Это – анализ
Поэт сказал однажды: «Весь мир в бокале вина». Мы, вероятно, никогда не поймем, какой смысл он в это вкладывал, ибо поэты пишут не для того, чтобы быть понятыми. Но бесспорно, что, внимательно взглянув в бокал вина, мы поистине откроем целый мир. В нем и физические явления (искрящаяся жидкость, испарение, меняющееся в зависимости от погоды и вашего дыхания, блеск стекла) и атомы (о которых нам говорит уже наше воображение). Стекло – это очищенная горная порода; в его составе кроются секреты возраста Вселенной и развития звезд. А из какого удивительного набора реактивов состоит это вино! Как они возникли? Там есть закваска, ферменты, вытяжки и разные другие продукты. Ведь в вине скрывается большое обобщение: вся жизнь есть брожение. Изучая химию вина, нельзя не открыть, как это и сделал Луи Пастер, причины многих болезней. Сколько жизни в этом кларете, если он навязывает нашему сознанию свой дух, если мы должны быть столь осторожны с ним! Наш ограниченный ум для удобства делит этот бокал вина, этот мир на части: физику, биологию, геологию, астрономию, психологию и т. д., но ведь природа на самом деле никакого деления не знает! Давайте же и мы сольем это воедино, не забывая все же, что мы увидели. Пусть этот бокал вина доставит напоследок еще одно наслаждение: выпить его и обо всем позабыть!
Глава 4 СОХРАНЕНИЕ ЭНЕРГИИ
§ 1. Что такое энергия?
С этой главы, покончив с общим описанием природы вещей, мы начнем подробное изучение различных физических вопросов. Чтобы показать характер идей и тип рассуждений, которые могут применяться в теоретической физике, мы разберем один из основных законов физики – сохранение энергии.
Существует факт, или, если угодно,
Познакомимся с мальчиком, этаким Монтигомо Ястребиный Коготь; у него есть большие кубики, которые даже он не может ни сломать, ни разделить на части. Все они одинаковы. Пускай их у него 28 штук. Мама оставляет его утром дома наедине с этими кубиками. Каждый вечер она подсчитывает, сколько у него кубиков, – она немного любопытна! – и открывает поразительную закономерность: что бы ее сынишка ни вытворял с кубиками, их все равно оказывается 28! Так это тянется довольно долго, и вдруг в один прекрасный день она насчитывает только 27 штук. После недолгих поисков кубик обнаруживают под ковром: ей приходится все обыскать, чтобы убедиться в неизменности числа кубиков. В другой раз кубиков оказывается 26. Снова тщательное исследование показывает, что окно отворено; взглянув вниз, она видит два кубика в траве. В третий раз подсчет дает 30 кубиков! Это приводит маму в полное замешательство, но потом она вспоминает, что в гости приходил соседский Кожаный Чулок, видимо, он захватил с собой свои кубики и позабыл их здесь. Она убирает лишние кубики, затворяет плотно окно, не пускает больше гостей в дом, и тогда все опять идет как следует, пока однажды подсчет не дает 25 кубиков… Правда, в комнате имеется ящик для игрушек, маме хочется и в него заглянуть, но мальчик кричит: «Не открывай мой ящик!» и начинает рёв; мама к ящику не допускается. Как же быть? Но мама любопытна и хитра, она придумывает выход! Она знает, что кубик весит 500 г; она взвешивает ящик, когда все 28 кубиков на полу, он весит 1
 |
Но опять возникают отклонения и от этой формулы. Снова в результате кропотливых изысканий выясняется, что при этом уровень воды в стиральной машине почему–то изменился. Дитя, оказывается, швыряет кубики в воду, а мать не может их увидеть – вода мыльная; но она может узнать, сколько в воде кубиков, добавив в формулу новый член. Первоначальный уровень воды 40
 |
Мир представлений мамы постепенно расширяется, она накопит весь ряд членов, позволяющих рассчитывать, сколько кубиков находится там, куда она заглянуть не может. В итоге она открывает сложную формулу для количества, которое
В чем же аналогия между этим примером и сохранением энергии? Самое существенное, от чего надлежит отвлечься в этой картинке, – это что
Важно понимать, что физике сегодняшнего дня неизвестно,
§ 2. Потенциальная энергия тяготения
Сохранение энергии можно понять, только если имеются формулы для всех ее видов. Я сейчас рассмотрю формулу для энергии тяготения близ земной поверхности; я хочу вывести ее, но не так, как она впервые исторически была получена, а при помощи специально придуманной для этой лекции нити рассуждений. Я хочу вам показать тот достопримечательный факт, что нескольких наблюдений и строгого размышления достаточно, чтобы узнать о природе очень и очень многое. Вы увидите, в чем состоит работа физика–теоретика. Вывод подсказан блестящими рассуждениями Карно о к. п. д. тепловых машин.
Рассмотрим грузоподъемные машины, способные подымать один груз, опуская при этом другой. Предположим еще, что
Очень простая грузоподъемная машина показана на фиг. 4.1.
 |
Она подымает тройной вес. На одну чашку весов помещают три единицы веса, на другую – одну. Правда, чтобы она и впрямь заработала, с левой чашки необходимо снять хоть малюсенький грузик. И наоборот, чтобы поднять единичный груз, опуская тройной, тоже нужно немного сплутовать и убрать с правой чашки часть груза. Мы понимаем, что в настоящей подъемной машине надо создать небольшую перегрузку на одну сторону, чтобы поднять другую. Но пока махнем на это рукой. Идеальные машины, хотя их и нет на самом деле, не нуждаются в перевесе. Машины, которыми мы фактически пользуемся, можно считать в некотором смысле
Представим, что имеются два класса машин –
Мы берем единичный вес и опускаем его на единицу длины машиной
Легко понять также, что все обратимые машины должны поднимать груз
Пусть у нас есть обратимая машина, способная поднимать 3
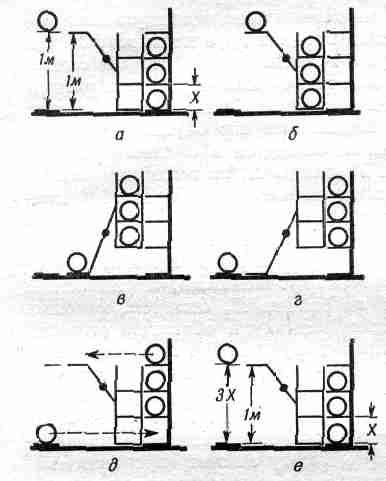 |
Четвертый лежит на подставке в одном метре от пола. Машина может поднять три шара, опустив один шар на 1
(Потенциальная энергия тяготениях для одного тела) = (Вес) x (Высота). (4.3)
Не правда ли, очень красивое рассуждение? Вопрос только в том, справедливо ли оно. (Ведь, в конце концов, природа
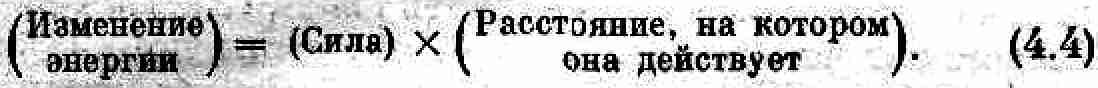 |
По мере чтения курса мы еще не раз будем возвращаться к другим видам потенциальной энергии.
Принцип сохранения энергии во многих обстоятельствах оказывается очень полезен при предсказании того, что может произойти. В средней школе мы учили немало правил о блоках и рычагах. Мы можем теперь убедиться, что все эти «законы»
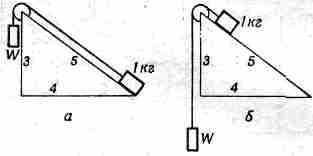 |
Подвесим к блочку груз весом 1
Мы хотим знать, какова должна быть тяжесть
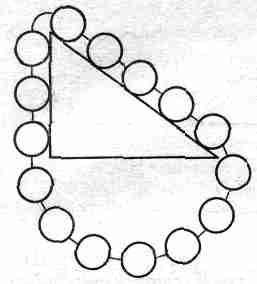 |
Глядя на диаграмму, становится очевидно, что
А вот задача посложнее: домкрат, показанный на фиг. 4.5.
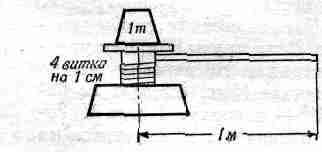 |
Посмотрим, как в таком случае применять этот принцип. Для вращения домкрата служит ручка длиной 1
И еще более сложный пример (фиг. 4.6).
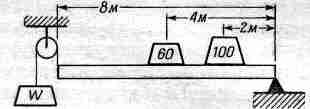 |
Подопрем один конец стержня (или рейки) длиной 8
— 4W+2x60+1x100=0,
Выходит, чтобы удержать рейку, хватит 55
§ 3. Кинетическая энергия
Чтобы рассказать о другом виде энергии, рассмотрим маятник (фиг. 4.7).
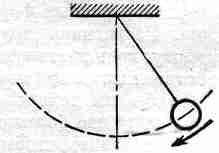 |
Отведем его в сторону и затем отпустим. Он начнет качаться взад и вперед. Двигаясь от края к середине, он теряет высоту. Куда же девается потенциальная энергия? Когда он опускается до самого низа, энергия тяготения пропадает, однако он вновь взбирается вверх. Выходит, что энергия тяготения должна превращаться в другую форму. Ясно, что способность взбираться наверх остается у маятника благодаря тому, что он
Мы должны получить формулу для энергии движения. Вспоминая наши рассуждения о необратимых машинах, мы легко поймем, что, двигаясь мимо наинизшей точки, маятник должен обладать некоторым количеством энергии, которая позволит ему подняться на определенную высоту, и при этом независимо от
к. э. =
Нам нужна формула, предсказывающая высоту подъема по быстроте движения тела. Если мы толкнем что–нибудь с определенной скоростью, скажем, прямо вверх, то это тело достигнет определенной высоты; мы не знаем пока, какова эта высота, но нам ясно, что она зависит от скорости и что она войдет в нужную нам формулу. Значит, чтобы найти формулу для кинетической энергии тела, движущегося со скоростью V, нужно вычислить высоту, до которой она может добраться, и умножить на тяжесть тела. В одной из следующих глав мы убедимся, что получается
к.э.=WV22g (4.6)
Конечно, тот факт, что движение обладает энергией, никак не связан с полем тяготения, в котором находится тело. Неважно,
§ 4. Прочие формы энергии
В таком вот роде можно и дальше показывать существование энергии в разных формах. Отметим, во–первых, упругую энергию. Растягивая пружину, мы должны совершить какую–то работу, ведь растянутая пружина способна поднять груз. После растяжения она получает возможность выполнить работу. Если бы мы теперь составили сумму произведений весов на высоты, то она больше не сошлась бы, и нам пришлось бы в нее что–то вставить, чтобы учесть напряженность пружинки. Упругая энергия – это и есть формула растянутой пружины. Сколько же в ней энергии?
Когда вы отпускаете пружину, то упругая энергия при переходе пружины через точку равновесия обращается в энергию кинетическую; и далее все время совершаются переходы от сжатия и растяжения пружины к кинетической энергии движения (в переходы эти замешиваются еще изменения энергии тяготения, но если это нам мешает, то можно пружину не подвешивать, а положить). И так продолжается до тех пор, пока потери энергии… Постойте! Выходит, мы все время жульничали: то совершали обвес, чтобы рычаг наклонился, то говорили, что машины обратимы, то уверяли, что они будут работать вечно. А машина в конечном счете останавливается. Где же теперь, когда пружина перестала сжиматься–разжиматься, находится энергия? Она перешла в
В пружине или рычаге имеются кристаллы, состоящие из множества атомов; и при сборке частей машины требуется особая точность и тщательность, чтобы в работе машины ни один из атомов не сдвинулся со своего места, не поколебался. Нужно быть очень осторожным. Ведь обычно, когда машина вертится, то и дело происходят какие–то удары, покачивания, вызванные неровностями материала, и атомы начинают дрожать. Так теряются маленькие доли энергии; по мере того как движение замедляется, все сильнее становятся случайные, неожиданные дрожания атомов вещества машины. Конечно, это все еще кинетическая энергия, но не связанная с видимым движением.
Позвольте, какая кинетическая энергия? Что за сказка? Откуда известно, что это все еще кинетическая энергия? Оказывается, термометр способен обнаружить, что пружина или рычаг
Существует еще немало других форм энергии, но мы не можем сейчас описывать их более или менее подробно.
Имеется энергия электрическая, связанная с притяжением и отталкиванием электрических зарядов.
Есть энергия излучения, или энергия света, – одна из форм электрической энергии, ибо свет может быть представлен как колебания электромагнитного поля.
Бывает энергия химическая – энергия, высвобождаемая в химических реакциях. Упругая энергия в некотором роде похожа на химическую; и химическая энергия есть энергия притяжения атомов друг к другу, и упругая энергия тоже. В настоящее время мы это понимаем следующим образом: химическая энергия складывается из двух частей – энергии движения электронов внутри атомов, т. е. из кинетической части, и электрической энергии притяжения электронов к протонам, т. е. из электрической части.
Дальше, бывает ядерная энергия, связанная с расстановкой частиц в ядре; для нее тоже существует формула, хотя основные законы нам и неведомы. Мы знаем, что это не электричество, не тяготение, не чистая химия… А что это такое? А кто его знает! Видимо, это добавочная форма энергии.
И наконец, теория относительности видоизменяет формулу кинетической энергии, так что название это становится условным, сочетая ее с другим понятием:
Из наших рассуждений ясно, что закон сохранения энергии незаменим при анализе явления; мы уже показали это на ряде примеров, для которых мы не знали всех формул. Владей мы формулами для всех типов энергии, мы могли бы узнавать, не вдаваясь в детали, сколько процессов происходит в таком–то явлении. Оттого законы сохранения столь важны. Встает естественный вопрос: какие еще есть в физике законы сохранения.
Существуют еще два закона, сходных с законом сохранения энергии. Один называется сохранением импульса (или количества движения). Другой – сохранением момента количества движения. Позже мы подробней познакомимся с ними.
В конечном счете мы не понимаем законов сохранения достаточно глубоко. Нам непонятно сохранение энергии. Мы не можем представить себе энергию как некоторое количество неделимых порций. Вы, вероятно, слышали, что фотоны вылетают порциями и что энергия их равна постоянной Планка, умноженной на частоту. Это правда, но так как частота света может быть любой, то нет никакого закона, по которому энергия обязана иметь некоторую определенную величину. Это уже не кубики Монтигомо Ястребиного Когтя: любые количества энергии допустимы, по крайней мере в настоящее время. Для нас энергия – это не то, что можно пересчитать, а всего лишь математическая величина, абстракция, – обстоятельство довольно странное. В квантовой механике выявляется, что сохраняемость энергии тесно увязана с другим важным свойством мира –
Кроме этого, существуют еще три закона сохранения; насколько ныне нам известно, они точные и понять их намного легче, так как по своей природе они близки к подсчету кубиков. Первый из них –
Вот вам шесть законов сохранения: три замысловатых, связанных с пространством и временем, а три простых, связанных с обычным счетом.
К сохраняемости энергии
Наконец, остановимся на том, откуда мы сегодня можем получать необходимый запас энергии. Энергией нас снабжают Солнце и дожди, уголь, уран и водород. Впрочем, и дожди, и уголь в конце концов без Солнца были бы невозможны. Хотя энергия сохраняется, природа, по всей видимости, этим ничуть не интересуется; она освобождает из Солнца множество энергии, но только одна двухмиллиардная часть ее падает на Землю. Природа сохраняет энергию, но в действительности о ней не заботится, расточая ее направо и налево. Мы уже получаем энергию из урана, мы можем получать ее и из водорода, но пока это получение связано со взрывами, с большой опасностью. Если бы мы смогли научиться управлять термоядерными реакциями, то энергия, которую можно получать, тратя по 10
Глава 5 ВРЕМЯ И РАССТОЯНИЕ
§ 1. Движение
В этой главе мы рассмотрим понятия
Многие считают, что физика берет свое начало с опыта, проведенного Галилеем 350 лет назад, а сам Галилей является первым физиком. До этого времени изучение движения было чисто философским и основывалось на доводах, которые были плодом фантазии. Большинство этих доводов были придуманы Аристотелем и другими греческими философами и рассматривались как «доказанные». Но Галилей был скептиком и поставил следующий опыт: по наклонной плоскости он пускал шар и наблюдал за его движением (фиг. 5.1).
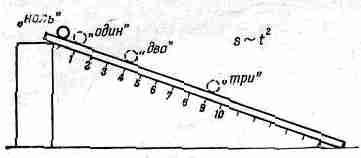 |
Галилей не просто смотрел, как катится шар, а измерял то
Будем отсчитывать удары пульса в то время, пока шарик катится вниз: «Один… два… три… четыре… пять… шесть… семь… восемь…». Пусть кто–нибудь отмечает положение шарика на каждый счет. Теперь можно измерить
S?t2
Таким образом, изучение процесса
§ 2. Время
Разберем сначала, что мы понимаем под словом
Однако, по–видимому, все дни в среднем одинаковы. Можно [и проверить, действительно ли они одинаковы и от одного дня до другого, хотя бы в среднем, проходит ли одно и то же время? Для этого необходимо произвести сравнение с каким–то другим периодическим процессом. Давайте посмотрим, как такое сравнение можно, например, провести с помощью песочных часов. С помощью таких часов мы можем создать периодический процесс, если будем стоять возле них день и ночь и переворачивать каждый раз, когда высыплются последние крупинки песка.
Если затем подсчитать число переворачиваний песочных часов от каждого утра до следующего, то можно обнаружить, что число «часов» (т. е. число переворачиваний) в разные дни различно. Кто же виноват в этом? Может быть, Солнце? Может быть, часы? А может, и то и другое? После некоторых размышлений можно прийти к мысли, что следует считать «часы» не от утра до утра, а от полудня до полудня (полдень – это, конечно, не 12 часов, а момент, когда Солнце находится в наивысшем положении). На этот раз оказывается, что в каждых сутках число «часов» одинаково.
Теперь можно утверждать, что «час» и «сутки» имеют регулярную периодичность, т. е. отмечают последовательные равные интервалы времени, хотя нами и
§ 3. Короткие времена
Заметим, что в процессе проверки «воспроизводимости» дней мы нашли метод измерения
Галилей предположил, что каждый маятник отклоняется и возвращается назад за равные интервалы времени (если отклонения невелики). Сравнение числа отклонений маятника с «часом» показывает, что это действительно так. Таким способом можно измерять доли «часа». Если для подсчета числа колебаний маятника применить механический счетчик, то мы получим маятниковые часы наших дедов.
Договоримся теперь, что если маятник отклонится 3600 раз в час (и если в сутках 24 часа), то период колебаний такого маятника мы назовем «секундой». Итак, нашу первоначальную единицу «сутки» мы разделили приблизительно на 105 частей. Используя тот же принцип сравнения, можно и секунду разделить на все меньшие и меньшие части. Для этого оказывается более удобным использовать не простой механический, а
Давайте представим себе целый ряд таких осцилляторов, что период колебаний каждого последующего в десять раз меньше предыдущего. Это можно проверить путем простого подсчета числа колебаний последующего осциллятора за одно колебание предыдущего; только теперь этот подсчет трудно провести без устройства, расширяющего возможности наблюдения, своеобразного «микроскопа времени». Таким устройством может служить электронно–лучевой осциллограф, на светящемся экране которого строится график зависимости электрического тока, (или напряжения) от времени.
Соединяя осциллограф сначала с одним осциллятором, а затем с другим, мы получим на экране графики зависимости тока от времени в одном и в другом осцилляторе (фиг. 5.2).
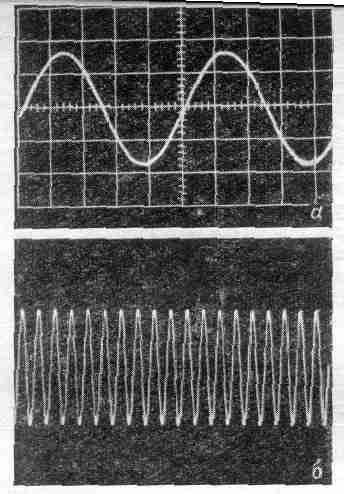 |
А теперь нетрудно подсчитать, какое число периодов «быстрого» осциллятора укладывается в одном периоде «медленного».
Современная электроника позволяет создавать осцилляторы с периодами 10–12
Можно измерять промежутки времени, гораздо более короткие, чем 10–12
Именно таким методом в последние годы измерялось время жизни ?0–мезона. При наблюдении в микроскоп мельчайших следов, оставленных на фотоэмульсии, в которой родился ?0–мезон, было обнаружено следующее: ?0–мезон, двигаясь со скоростью, близкой к скорости света, прежде чем распасться, проходит в среднем расстояние около 10–7
Развивая технику эксперимента, а если необходимо, меняя определение понятия «время», можно обнаружить еще более быстрые физические процессы. Мы, например, можем говорить о периоде вибраций ядра или о времени жизни недавно обнаруженных «странных» резонансов (частиц), которые уже упоминались в гл. 2. Время жизни этих частиц лишь ненамного больше 10–24 сек! Приблизительно столько времени требуется свету (который имеет наибольшую скорость распространения), чтобы пройти расстояние, равное диаметру ядра водорода (наименьший из известных объектов).
Что можно сказать о еще более коротких интервалах времени? Имеет ли смысл вообще говорить о них, если невозможно не только измерить, но даже разумно судить о процессах, происходящих в течение столь коротких интервалов? Возможно, нет. Это один из тех вопросов, на которые нет ответа. Может быть, кому–нибудь из вас посчастливится ответить на него в ближайшие 20–30 лет.
§ 4. Большие времена
Рассмотрим теперь промежутки времени, большие «суток». Измерять большие времена легко: нужно просто считать дни, пока не придумаем что–нибудь лучшего. Первое, с чем мы сталкиваемся, это год – вторая естественная периодичность, состоящая приблизительно из 365 дней. Интересно, что в природе существуют естественные счетчики лет в виде годовых колец у деревьев или отложений речного ила. В некоторых случаях можно использовать эти естественные счетчики для определения времени, отделяющего нас от какого–либо отдаленного события в прошлом.
 |
Но, когда невозможно считать годы для очень больших отрезков времени, нужно искать какие–то другие способы измерения. Одним из наиболее эффективных методов является использование в качестве «часов» радиоактивного вещества. Здесь мы сталкиваемся с «регулярностью» иного рода, чем в случае, скажем, маятника. Радиоактивность любого вещества для последовательных равных
Если начертить график зависимости радиоактивности от времени, то мы получим кривую типа изображенной на фиг. 5.3.
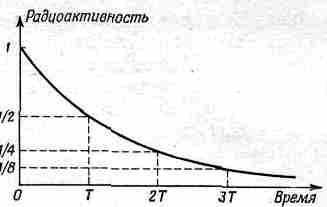 |
Мы видим, что если радиоактивность за
Если мы знаем, что какой–то материал, например дерево, при своем образовании содержал некоторое количество
(1/2)t/T=B/A.
А такие случаи, когда мы знаем первоначальное количество радиоактивного вещества, к счастью, существуют. Известно, например, что углекислый газ в воздухе содержит малую долю радиоактивного изотопа С14, период полураспада которого составляет 5000 лет. Количество его благодаря действию космических лучей постоянно пополняется взамен распавшегося. Если мы измеряем
Хотелось бы, однако, узнать возраст еще более древних вещей. Это можно сделать, измерив содержание других радиоактивных элементов с большими периодами полураспада. Уран, например, имеет изотоп с периодом полураспада около 109 лет, так что если какой–то материал при своем образовании 109 лет назад содержал уран, то сегодня от него осталась только половина первоначального количества. При своем распаде уран превращается в свинец. Как определить возраст горной породы, которая образовалась много–много лет назад в результате какого–то химического процесса? Свинец по своим химическим свойствам отличается от урана, поэтому они первоначально входили в разные виды горных пород. Если взять такой вид породы, который вначале должен был содержать только уран, то мы обнаружим в нем некоторое количество свинца. Сравнивая доли свинца и урана, можно определить ту часть урана, которая в результате распада превратилась в свинец. Этим методом было установлено, что возраст некоторых горных пород составляет несколько миллиардов лет. Применяя шире этот метод путем сравнения содержания урана и свинца не только в некоторых горных породах, но и в воде океанов, а затем усредняя различные данные по всему земному шару, установили, что нашей планете исполнилось примерно 5,5 миллиарда лет.
Интересно, что возраст метеоритов, падающих на Землю, вычисленный по урановому методу, совпадает с возрастом самой Земли. Более того, оказалось, что и метеориты, и горные породы Земли составлены из одного и того же материала, поэтому существует мнение, что Земля образовалась из пород, «плававших» некогда в «околосолнечном» пространстве.
Некогда, во времена, еще более древние, чем возраст Земли (т. е. 5 миллиардов лет назад), начала свою историю Вселенная. Сейчас считают, что возраст по крайней мере нашей части Вселенной достигает примерно 10–12 миллиардов лет. Нам неизвестно, что было до этого. В сущности опять можно спросить: «А есть ли смысл говорить о том, что было до этого? И имеет ли смысл само понятие «время» до «рождения» Вселенной?»
§ 5. Единицы и стандарты времени
Мы уже говорили, что счет времени удобно вести в каких–то стандартных единицах, скажем в днях или секундах, и измерять длительности в количествах этой единицы или ее долях. Но что же выбрать за основную стандартную единицу? Можно ли, например, принять за отправную единицу человеческий пульс? Очевидно, нет. Уж очень непостоянна эта единица. Лучше обстоит дело с часами. Двое часов согласуются гораздо лучше, чем пульс. Вы скажете: ладно, давайте возьмем часы. Но чьи? Существует предание об одном швейцарском мальчике, которому хотелось, чтобы все часы в его городе отзванивали полдень и в одно и то же время. Он ходил по городу и доказывал всем, насколько это важно. Каждый считал, что это действительно было бы чудесно, если бы все другие часы в городе звонили полдень по
Вплоть до самого последнего времени не было найдено ничего более точного, чем вращение Земли, и поэтому все часы сверялись с длиной астрономических суток, а секунда определялась как 1/86 400 часть средних суток. Однако сейчас мы научились работать с некоторыми естественными осцилляторами, которые являются более точными стандартами времени, чем вращение Земли. Это так называемые «атомные часы». В основе их лежат колебания атомов, период которых нечувствителен к температуре и другим внешним воздействиям. Эти часы позволяют измерять время с точностью, лучшей 10–7%. В последние два года профессор Гарвардского университета Норман Рамзей спроектировал и построил улучшенные атомные часы, работающие на колебаниях атомов водорода. Он считает, что эти часы могут быть еще в сто раз более точными. Сейчас ведутся измерения, которые покажут, насколько он прав.
А поскольку оказалось возможным создать часы гораздо более точные, чем астрономические, то ученые договариваются определять единицу времени с помощью новых стандартов – атомных часов.
§ 6. Большие расстояния
Вернемся теперь к вопросу о
Однако под расстоянием мы понимаем не только то, что можно измерить метром. Как, например, измерить метром расстояние между вершинами двух гор? Здесь на помощь приходит уже другой метод измерения расстояний – триангуляция. Хотя это означает использование другого определения понятия «расстояние», но в тех случаях, когда есть возможность применить оба метода, они дают одинаковый результат. Пространство все же более или менее соответствует представлениям Евклида, поэтому оба определения эквивалентны. Ну, а раз они согласуются на Земле, то мы более уверены в законности применения триангуляции и для больших расстояний. Этим методом была измерена, например, высота первого спутника (фиг. 5.4).
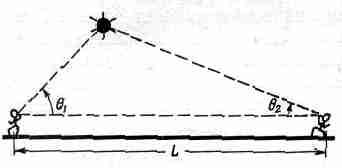 |
Она оказалась равной приблизительно 5•105
В последний год достигнуты большие успехи в определении масштаба солнечной системы. В Лаборатории ракетных двигателей с помощью прямой радиолокационной связи были проведены очень точные измерения расстояния от Земли до Венеры. Здесь мы имеем дело еще с одним определением понятия «расстояние». Нам известна скорость распространения света (а стало быть, и скорость распространения радиоволн), и мы предполагаем, что эта скорость постоянна на всем протяжении между Землей и Венерой. Послав радиоволну по направлению к Венере, мы считаем время до прихода обратно отраженной волны. А зная
А как измерить расстояние до еще более отдаленных объектов, например до звезд? К счастью, здесь снова можно возвратиться к нашему методу триангуляции, ибо движение Земли вокруг Солнца позволяет измерить расстояние до объектов, находящихся вне солнечной системы. Если мы направим телескоп на некую звезду один раз зимой, а другой раз летом (фиг. 5.5), то можно надеяться достаточно точно измерить углы и определить расстояние до этой звезды.
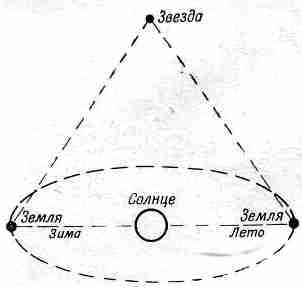 |
Но что делать, если звезда находится настолько далеко от нас, что уже невозможно пользоваться методом триангуляции? Астрономы всегда изобретают все новые и новые способы определения расстояний. Так, они научились определять размер и яркость звезд по их цвету. Оказалось, что цвет и истинная яркость многих близлежащих звезд, расстояние до которых определялось методом триангуляции, в большинстве случаев связаны между собой гладкой зависимостью. Если теперь измерить цвет отдаленной звезды, то по этой зависимости можно определить ее истинную яркость, а измеряя
 |
Достаточно взглянуть на фотографию, чтобы убедиться, что все эти звезды расположены в одном месте. Тот же результат получается и с помощью метода сравнения цвета и яркости.
Изучение многих шаровых скоплений дает еще одну важную информацию. Оказалось, что существует участок неба с большой концентрацией таких шаровых скоплений, причем большинство из них находится на одном и том же расстоянии от нас. Сравнивая эти данные с некоторыми другими, мы приходим к заключению, что эти скопления являются центром нашей Галактики. Таким образом мы определяем, что расстояние до центра Галактики составляет приблизительно 1020
Данные о размере нашей Галактики дают ключ к определению еще больших межгалактических расстоянии. На фиг. 5.7 приведена фотография галактики, которая по форме очень похожа на нашу Галактику.
 |
Возможно, что и размер ее тот же. (Есть еще ряд соображений, согласно которым размеры всех галактик приблизительно одинаковы.) А если это так, то можно узнать расстояние до нее. Мы измеряем угловой размер галактики (т. е. угол, который она занимает на небесном своде), знаем ее диаметр, а стало быть, можем вычислить расстояние. Опять триангуляция!
Недавно с помощью гигантского Паломарского телескопа были получены фотографии неимоверно далеких галактик. Одна из этих фотографий приведена на фиг. 5.8.
 |
Сейчас полагают, что расстояние до некоторых из них приблизительно равно половине размера Вселенной (1026
§ 7. Малые расстояния
Обратимся теперь к малым расстояниям. Подразделить метр просто. Без особых трудностей можно разделить его на тысячу равных частей. Таким же путем, хотя и несколько сложнее (используя хороший микроскоп), можно разделить миллиметр на тысячу частей и получить микрон (миллионную долю метра). Однако продолжать это деление становится трудно, поскольку невозможно «увидеть» объекты, меньшие, чем длина волны видимого света (около 5?10–7
Все же мы не останавливаемся на том, что недоступно глазу. С помощью электронного микроскопа можно получить фотографии, помогающие увидеть и измерить еще меньшие объекты – вплоть до 10–8
 |
А с помощью косвенных измерений (своего рода триангуляции в микроскопическом масштабе) можно измерять все меньшие и меньшие объекты. Сначала из наблюдений отражения света короткой длины волны (рентгеновских лучей) от образца с нанесенными на известном расстоянии метками измеряется длина волны световых колебаний.
 |
Затем по картине рассеяния того же света на кристалле можно определить относительное расположение в нем атомов, причем результат хорошо согласуется с данными о расположении атомов, полученными химическим путем. Таким способом определяется диаметр атомов (около 10–10
Дальше в шкале расстояний имеется довольно большая незаполненная «щель» между атомными размерами 10–10
Эффективные сечения ядер можно определить, пропуская пучок частиц высокой энергии через тонкую пластинку вещества и измеряя число частиц, не прошедших сквозь нее. Эти высокоэнергетические частицы прорываются сквозь легкое облачко электронов, но при попадании в тяжелое ядро останавливаются или отклоняются. Предположим, что у нас имеется пластинка толщиной 1
 |
Фиг. 5.10. Воображаемая пластинка углерода толщиной 1 см при сильном увеличении (если бы были видны только ядра атомов).
Вероятность того, что очень малая частица столкнется с ядром, равна отношению площади, занимаемой ядрами (черные точки), к общей площади рисунка. Пусть над областью с площадью
?r2=?=ANn1–n2n1.
Из таких экспериментов мы находим, что радиусы ядер лежат в пределах от 1?10–15 до 6?10–15
Что можно ожидать в области еще меньших расстояний? Можно ли их измерять? На этот вопрос пока еще нет ответа. Может быть, именно здесь, в каком–то изменении понятия пространства или измерения на малых расстояниях, кроется разгадка тайны ядерных сил.
Несколько слов о стандарте длины. Разумно в качестве стандарта использовать какую–то естественную единицу длины, например радиус Земли или некоторую его долю. Именно таким образом возник метр. Первоначально он определялся как (?/2)?10–7 доля радиуса Земли. Однако такое определение нельзя считать ни особенно точным, ни удобным. Поэтому в течение долгого времени по международному соглашению в качестве эталона метра принималась длина между двумя метками, сделанными на особом брусе, который хранится в специальной лаборатории во Франции. Только много позднее поняли, что и такое определение метра не столь уж точно, как это необходимо, и не так уж универсально и постоянно, как этого хотелось бы. Поэтому сейчас принят новый стандарт длины как некоторое заранее установленное число длин волн определенной спектральной линии.
• • •
Результаты измерения расстояний и времени зависят от наблюдателя. Два наблюдателя, движущиеся друг относительно друга, измеряя один и тот же предмет или длительность одного и того же процесса, получат разные значения, хотя, казалось бы, мерили одно и то же. Расстояния и интервалы времени в зависимости от системы координат (т. е. системы отсчета), в которой производят измерения, имеют различную величину. В последующих главах мы будем более подробно разбирать этот вопрос.
Законы природы не позволяют выполнять абсолютно точные измерения расстояний или интервалов времени. Мы уже упоминали ранее, что ошибка в определении положения предмета не может быть меньше, чем
?x=h?p,
где
Относительность пространства и времени приводит к тому, что измерения интервалов времени также не могут быть точнее, чем
?t=h?E,
где ?E – ошибка в измерении энергии того процесса, продолжительностью которого мы интересуемся. Чтобы знать
Глава 6 ВЕРОЯТНОСТЬ
Истинная логика нашего мира–это подсчет вероятностей.
§ 1. Вероятность и правдоподобие
«Вероятность», или «шанс», – это слово вы слышите почти ежедневно. Вот по радио передают прогноз погоды на завтра: «Вероятно, будет дождь». Вы можете сказать: «У меня мало шансов дожить до ста лет». Ученые тоже часто употребляют эти слова. Сейсмолога интересует вопрос: какова вероятность того, что в следующем году в Южной Калифорнии произойдет землетрясение такой–то силы? Физик может спросить: с какой вероятностью этот счетчик Гейгера зарегистрирует двадцать импульсов в последующие десять секунд? Дипломата или государственного деятеля волнует вопрос: каковы шансы этого кандидата быть избранным президентом? Ну, а вас, конечно, интересует: есть ли шансы что–либо понять в этой главе?
Под
Иногда мы строим догадки потому, что хотим при ограниченности своих знаний сказать как можно
Давайте рассмотрим классический пример с подбрасыванием монеты. Если монета «честная», то мы не можем знать наверняка, какой стороной она упадет. Однако мы предчувствуем, что ври большом числе бросаний число выпадений «орла» и «решки» должно быть приблизительно одинаковым. В этом случае говорят: вероятность выпадения «орла» равна половине.
Мы можем говорить о вероятности исхода только тех наблюдений, которые собираемся проделать в будущем.
PA=NA/N (6.1)
Наше определение требует некоторых комментариев. Прежде всего мы говорим о вероятности какого–то события только в том случае, если оно представляет собой возможный результат испытания, которое можно
Вы, конечно, можете возразить, что никакая ситуация не может повториться в
Хочу отметить, что я
Отмечу еще одну «субъективную» сторону нашего определения вероятности. Мы говорили, что NA – это «наша оценка наиболее вероятного числа случаев». При этом, конечно, мы не надеялись, что число нужных нам случаев будет
Но почему все же число 15 более правдоподобно, чем все остальные? Можно рассуждать следующим образом: если наиболее вероятное число выпадений «орла» будет N0
Наши рассуждения можно обобщить на
Пусть, например, в закрытом ящике находятся семь шаров разного цвета и мы наугад, т. е. не глядя, берем один из них. Вероятность того, что у нас в руке окажется красный шар, равна 1/7. Вероятность того, что мы из колоды в 36 карт вытащим даму пик, равна 1/36, такая же, как и выпадение двух шестерок при бросании двух игральных костей.
• • •
В гл. 5 мы определяли размер ядра с помощью затеняемой им площади или так называемого эффективного сечения. По существу речь шла о вероятностях. Если мы «обстреливаем» быстрыми частицами тонкую пластинку вещества, то имеется некая вероятность, что они пройдут через нее, не задев ядер, однако с некоторой вероятностью они могут попасть в ядро. (Ведь ядра столь малы, что мы не можем
NC/N=?/A. (6.2)
Поэтому можно сказать, что
Pc=n?/A, (6.3)
где n/A – просто число атомов, приходящихся на единицу площади пластинки.
§ 2. Флуктуации
Теперь мне бы хотелось несколько подробнее показать, как можно использовать идею вероятности, чтобы ответить на вопрос: сколько же в самом деле я
 |
Последовательности выпадений «орла» и «решки» показаны в том порядке, как это происходило. В первый раз получилось 11 выпадений «орла», во второй – тоже 11, а в третий – 16. Можно ли на этом основании подозревать, что монета была «нечестной»? Или, может быть, мы ошиблись, приняв 15 за наиболее вероятное число выпадений «орла» в каждой серии испытаний?
Сделаем еще 97 серий, т. е. 100 серий по 30 испытаний в каждой. Результаты их приведены в табл. 6.1.
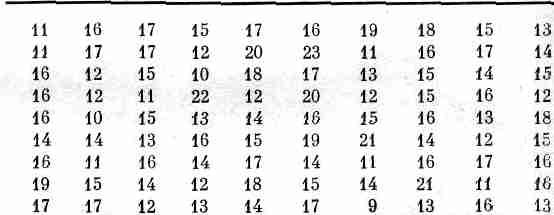 |
Проведено несколько серий испытаний, по 30 подбрасываний монеты в каждой
Взгляните на числа, приведенные в этой таблице. Вы видите, что большинство результатов «близки» к 15, так как почти все они расположены между 12 и 18. Чтобы лучше прочувствовать эти результаты, нарисуем график их
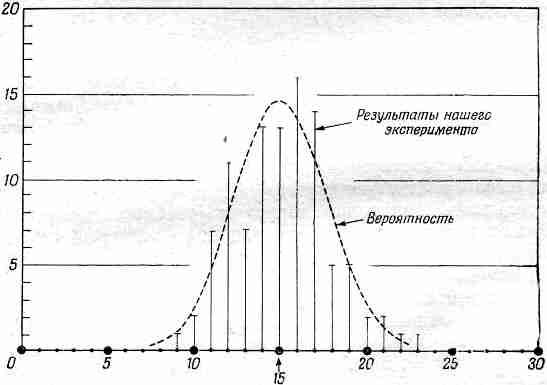 |
Действительно, в 13 сериях было получено 15 выпадений «орла», то же число серий дало 14 выпадений «орла»; 16 и 17 выпадений получались
Можно спросить: а какова вероятность того, что в серии из 30 испытаний «орел» выпадет 15 раз или 16, или какое–то другое число раз? Мы говорим, что вероятность выпадения «орла» в серии из
Рассмотрим теперь серию из трех испытаний. Третье испытание с равной вероятностью может дать либо «орел», либо «решку», поэтому существует только один способ получения трех выпадений «орла»: мы
Эти результаты удобно записать в виде диаграммы (фиг. 6.3).
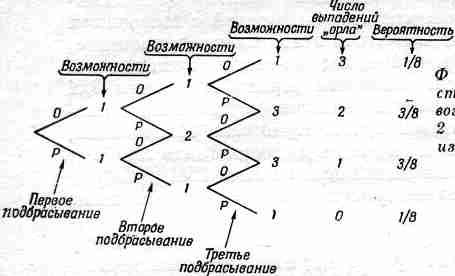 |
Фиг. 6.3. Диаграмма, иллюстрирующая число различных возможностей получения 0, 1, 2 и 3 выпадений «орла» в серии из трех испытаний.
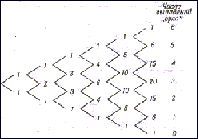 |
Ясно, что эту диаграмму можно продолжить, если мы интересуемся еще большим числом испытаний. На фиг. 6.4 приведена аналогичная диаграмма для шести испытаний.
Фиг. 6.4. Диаграмма, подобная изображенной на фиг. 6.3, для серии из шести испытаний.
Число «способов», соответствующих каждой точке диаграммы, – это просто число различных «путей» (т. е., попросту говоря, последовательность выпадения «орла» и «решки»), которыми можно прийти в эту точку из начальной, не возвращаясь при этом назад, а высота этой точки дает общее число выпадений «орла». Этот набор чисел известен под
испытаний, а k – число выпадений «орла». Отмечу попутно, что биномиальные коэффициенты можно вычислять по формуле:
(kn)=n!k!(n! — k!), (6.4)
где символ n!
Pk,n=(kn)2n (6.5)
Поскольку Pk,n – доля тех серий испытаний, в которых выпадение «орла» ожидается
Использованный здесь метод можно применять и в более общей ситуации, где в каждом единичном испытании возможны только два исхода, которые давайте обозначим через В (выигрыш) и П (проигрыш). Вообще говоря, вероятности В и П в каждом отдельном испытании могут быть разными. Пусть
Pk,n=(kn)pkqn–k (6.6)
Эта функция вероятностей называется
§ 3. Случайные блуждания
Существует еще одна интересная задача, при решении которой не обойтись без понятия вероятности. Это проблема «случайных блужданий». В простейшем варианте эта задача выглядит следующим образом. Вообразите себе игру, в которой игрок, начиная от точки
Прежде всего давайте рассмотрим несколько примеров случайных блужданий. Их можно описать «чистым» продвижением DN
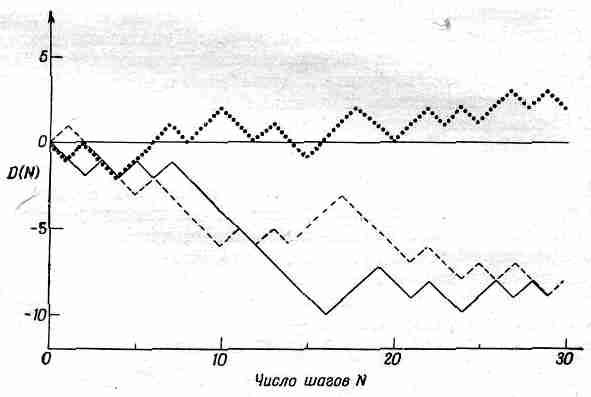 |
Фиг. 6.5. Три примера случайного блуждания.
(При построении их в качестве случайной последовательности решений о том, куда сделать следующий шаг, использовались результаты подбрасывания монеты, приведенные на фиг. 6.1.)
Что можно сказать о таком движении? Ну, во–первых, можно спросить: как далеко мы в среднем продвинемся? Нужно
Можно показать, что ожидаемая величина DN2 равна просто N – числу сделанных шагов. Кстати, под «ожидаемой величиной» мы понимаем наиболее вероятное значение (угаданное наилучшим образом), о котором можно думать как об
Ожидаемая величина DN2 для
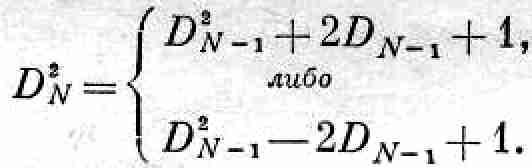 |
(6.7)
Если процесс повторяется большое число раз, то мы ожидаем, что каждая из этих возможностей осуществляется с вероятностью ?/2, так что средняя ожидаемая величина будет просто средним арифметическим этих значений, т. е. ожидаемая величина DN2 будет просто DN–12+1. Но какова величина DN–12
lt;DN2gt;=lt;DN–12gt;+1. (6.8)
Если теперь вспомнить, что lt;D12gt;=1, то получается очень простой результат:
lt;DN2gt;=1
Отклонение от начального положения можно характеризовать величиной типа расстояния (а не квадрата расстояния); для этого нужно просто извлечь квадратный корень из lt;DN2gt; и получить так называемое «среднее квадратичное расстояние» DC–K
DC–K=lt;D2gt;=N. (6.10)
Мы уже говорили, что случайные блуждания очень похожи на опыт с подбрасыванием монет, с которого мы начали эту главу. Если представить себе, что каждое продвижение вперед или назад обусловливается выпадением «орла» или «решки», то DN будет просто равно N0–Np
Отклонение N0 от ожидаемой величины
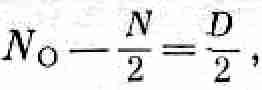 |
(6.11)
откуда для среднего квадратичного отклонения получаем
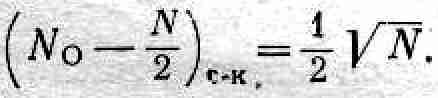 |
(6.12)
Вспомним теперь наш результат для DC–K
Теперь мы способны рассмотреть вопрос, которого избегали до сих пор. Как узнать, «честна» ли наша монета? Сейчас мы можем, по крайней мере частично, ответить на него. Если монета «честная», то мы ожидаем, что в половине случаев выпадет «орел», т. е.
lt;N0gt;/N=0,5. (6.13)
Одновременно ожидается, что действительное число выпадений «орла» должно отличаться от N/2 на величину порядка N/2, или, если говорить о
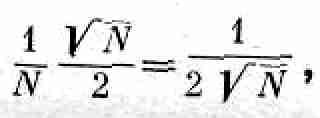 |
т. е. чем больше
На фиг. 6.6 отложены числа N0/N для тех подбрасываний монеты, о которых мы говорили раньше.
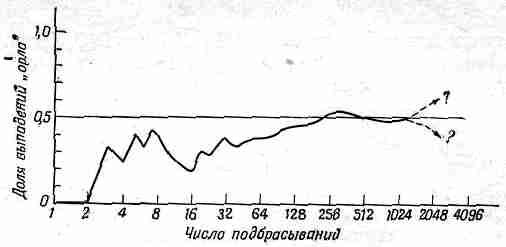 |
Как видите, при увеличении числа
Мы не рассматривали еще случаи, когда для монеты или какого–то другого объекта испытания, подобного монете (в том смысле, что возможны два или несколько достоверно не предсказуемых исхода наблюдения, например камень, который может упасть только на какую–то из двух сторон), имеется достаточно оснований полагать, что вероятности разных исходов не равны. Мы определили вероятность
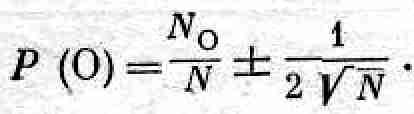 |
(6.14)
При такой записи подразумевается, что существует некая «истинная» вероятность, которую в принципе
§ 4. Распределение вероятностей
Давайте вернемся к проблеме случайных блужданий, но теперь уже с некоторым изменением. Пусть в дополнение к случайному выбору
lt;DN2gt;=lt;DN–12gt;+lt;S2gt;=lt;DN–12gt;+1. (6.15)
Так что, как и прежде,
lt;DN2gt;=N. (6.16)
Каково же в этом случае будет распределение расстояний! Какова, например, вероятность того, что после 30 шагов
Если же, однако, не требовать, чтобы
Р (х, ?x)=р(х)?x. (6.17)
Функция
Вид кривой
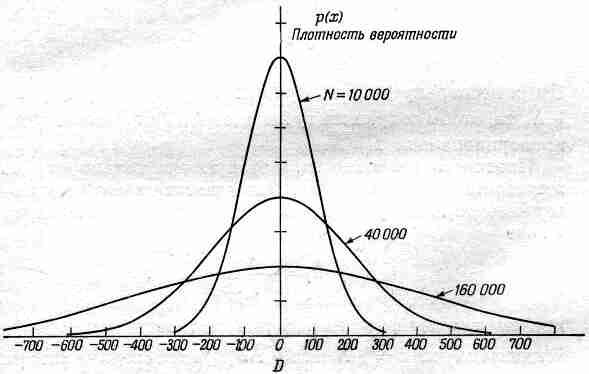 |
Заметьте, что «полуширины» этих кривых, как это и должно быть по нашим предыдущим расчетам, приблизительно равны N
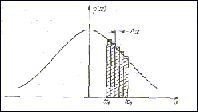 |
Вы, вероятно, заметили также, что величина
Геометрически эта вероятность [запишем ее в виде P(x1lt;Dlt;x2)] равна площади заштрихованной области на фиг. 6.8. При этом чем уже будут наши полоски, тем точнее результат. Поэтому можно записать
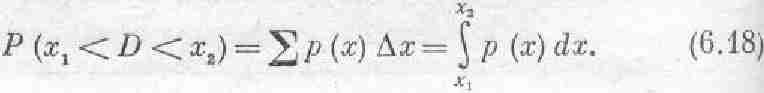 |
Площадь же ограничения всей кривой просто равна вероятности того, что
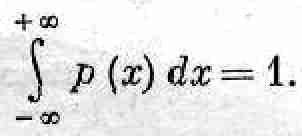 |
(6.19)
Ну а поскольку ширина кривых на фиг. 6.7 пропорциональна N, то, чтобы сохранить ту же площадь, их высота должна быть пропорциональна 1/N.
Плотность вероятности, которую мы только что описали, встречается наиболее часто. Она известна также под названием
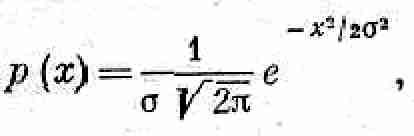 |
(6.20)
причем величина ? называется
В нашем случае ?=N или NSC–K
Мы уже говорили о том, что движения молекул или каких–то других частиц в газе похожи на случайные блуждания. Представьте себе, что мы открыли в комнате пузырек с духами или каким–то другим органическим веществом. Тотчас же молекулы его начнут испаряться в воздух. Если в комнате есть какие–то воздушные течения, скажем циркуляция воздуха, то они будут переносить с собой пары этого вещества. Но даже
Вы знаете, что давление газа вызывается тем, что молекулы его бомбардируют стенки сосуда. Позднее, когда мы подойдем к количественному описанию этого явления, нам понадобится знать, с какой скоростью движутся молекулы, ударяясь о стенку, поскольку сила их ударов зависит от скорости. Однако говорить о какой–то
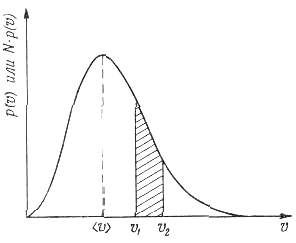 |
Фиг. 6.9. Распределение молекул газа по скоростям.
Скорость может иметь любую величину, однако больше шансов за то, что она окажется где–то в окрестности наиболее вероятного или ожидаемого значения lt;vgt;.
О кривой, показанной на фиг. 6.9, часто говорят в несколько ином смысле. Если мы возьмем газ, заключенный в каком–то сосуде (скажем, объемом 1
Поэтому
§ 5. Принцип неопределенности
Понятия вероятности оказались очень полезны при описании поведения газа, состоящего из огромного количества молекул. Немыслимо же в самом деле пытаться определить положение и скорость каждой из 1022 молекул! Когда впервые теория вероятности была применена к таким явлениям, то это рассматривалось просто как удобный способ работы в столь сложной обстановке. Однако теперь мы полагаем, что вероятность
Для описания местоположения частицы можно ввести плотность вероятности p1(x)
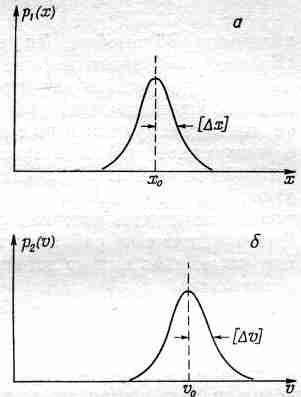 |
Точно такое же положение и со скоростью частицы: она тоже неизвестна нам точно. С некоторой вероятностью p2(v)?v частица может двигаться со скоростью, находящейся в интервале между v и v+?v.
Один из основных результатов квантовой механики состоит в том, что эти две плотности
[?x][?v]gt;=h/m (6.22)
и называется
Чтобы это соотношение выполнялось, частица должна себя вести очень курьезно. Вы видите, что правая часть соотношения (6.22) постоянна, а это означает, что если мы попытаемся «приколоть» частицу в каком–то определенном месте, то эта попытка окончится тем, что мы не сможем угадать, куда она летит и с какой скоростью. Точно также если мы попытаемся заставить частицу двигаться очень медленно или с какой–то
Принцип неопределенности выражает ту неясность, которая должна существовать при любой попытке описания природы. Наиболее точное и полное описание природы должно быть только вероятностным. Однако некоторым физикам такой способ описания приходится не по душе. Им кажется, что о
Эта присущая миру неопределенность в определении положения частицы является наиболее важной чертой описания структуры атомов. В атоме водорода, например, который состоит из одного протона, образующего ядро, и электрона, находящегося где–то вне его, неопределенность в местонахождении электрона такая же, как и размеры самого атома! Мы не можем поэтому с уверенностью сказать, где, в какой части атома находится наш электрон, и уж, конечно, не может быть и речи ни о каких «орбитах». С уверенностью можно говорить только
Это – колоколообразная функция наподобие изображенной на фиг. 6.8, причем число
Если вы хотите как–то представить себе атом водорода, то вообразите этакое «облако», плотность которого пропорциональна плотности вероятности. Пример такого облака показан на фиг. 6.11.
 |
Такая наглядная картинка, пожалуй, наиболее близка к истине, хотя тут же нужно помнить, что это
В своем стремлении узнать о природе вещей как можно больше современная физика обнаружила, что существуют вещи, познать которые точно ей никогда не удастся. Многому из наших знаний суждено навсегда остаться неопределенным. Нам дано знать
* Эти последние 97 экспериментов проводились следующим образом. Ящик, в котором находились 30 монет, энергично встряхивался; затем подсчитывалось число выпадений «орла».
Глава 7 ТЕОРИЯ ТЯГОТЕНИЯ
§ 1. Движение планет
В этой главе речь пойдет об одном из самых далеко идущих обобщений, сделанных когда–либо человеческим разумом. Мы заслуженно восхищаемся умом человека, но неплохо было бы постоять некоторое время в благоговении и перед
F=Gmm'r2
Если к этому добавить, что любое тело реагирует на приложенную к нему силу ускорением в направлении этой силы, по величине обратно пропорциональным массе тела, то способному математику этих сведений достаточно для вывода всех дальнейших следствий.
Но поскольку, как мы предполагаем, вы еще не столь талантливы, вооружим вас не только этими двумя аксиомами. Давайте вместе разберем следствия из них. Мы изложим вкратце историю открытия закона тяготения, остановимся на некоторых выводах из него и на его влиянии на историю, на загадках этого закона и на уточнении его Эйнштейном; мы «хотим еще обсудить связь закона тяготения с другими законами физики. Всего этого в одну главу не уложишь, но в надлежащих местах других глав мы снова будем возвращаться к этому.
История начинается с древних; наши предки наблюдали движение планет среди звезд и в конце концов поняли, что планеты движутся вокруг Солнца – факт, заново открытый позже Коперником. Немного больше труда потребовалось, чтобы открыть,
§ 2. Законы Кеплера
Прежде всего Кеплер понял, что все планеты движутся вокруг Солнца по кривой, называемой
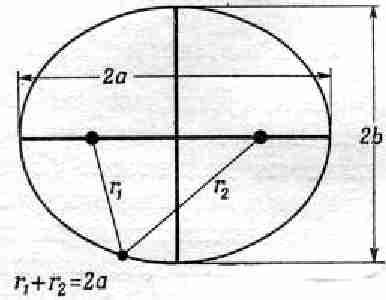 |
Другое наблюдение Кеплера состояло в том, что планеты движутся не с постоянной скоростью: поблизости от Солнца– быстрее, а удаляясь – медленнее. Более точно: пусть планета наблюдается в два последовательных момента времени, скажем на протяжении недели, и к каждому положению планеты проведен радиус–вектор. Дуга орбиты, пройденная планетой за неделю, и два радиус–вектора ограничивают некоторую площадь, заштрихованную на фиг. 7. 2.
 |
Если такие же наблюдения в течение недели проделать в другое время, когда планета движется по дальнему участку орбиты (т. е. медленнее), то построенная таким же способом фигура окажется по площади равной прежней. Итак, в соответствии со вторым законом орбитальная скорость любой планеты такова, что радиус «заметает» равные площади в равные интервалы времени.
Третий закон был открыт Кеплером гораздо позже; он другого рода, нежели первые два: он уже касается не одной планеты, а связывает между собой разные планеты. Закон утверждает, что если сравнить между собой период обращения и размеры орбиты двух планет, то периоды пропорциональны полуторной степени размеров орбит. Здесь период – это время, нужное планете для того, чтобы обойти всю орбиту; размер же измеряется длиной наибольшего диаметра эллиптической орбиты, ее большой оси. Считая орбиты кругами (чем они почти и являются), можно сказать проще: время одного оборота по кругу пропорционально его диаметру (или радиусу) в степени 32. Итак, три закона Кеплера таковы:
1. Все планеты движутся вокруг Солнца по эллипсу, в одном из фокусов которого находится Солнце.
2. Радиус–вектор от Солнца до планеты «заметает» равные площади в равные интервалы времени.
3. Квадраты времен обращения двух планет пропорциональны кубам больших полуосей их орбит: T2~a3
§ 3. Развитие динамики
В то время, когда Кеплер открывал эти законы, Галилей изучал законы движения. Он пытался выяснить, что заставляет планеты двигаться. (В те дни одна из предлагавшихся теорий утверждала: планеты движутся потому, что за ними летят невидимые ангелы, которые взмахами своих крыльев гонят планеты вперед. Ныне эта теория, как вы вскоре увидите, несколько видоизменена! По–видимому, чтобы заставить планеты вращаться, невидимые ангелы обязаны витать во всевозможных направлениях и обходиться без крыльев. В остальном эти теории схожи!) И Галилей открыл одно знаменательное свойство движения, достаточное, чтобы понять эти законы. Это – принцип
Ньютон затем видоизменил эту мысль, говоря, что единственный способ изменить движение тела – это применить
§ 4. Ньютонов закон тяготения
Лучше других поняв природу движения, Ньютон прикинул, что именно
Кроме того, из анализа третьего закона Кеплера можно вывести, что чем дальше от Солнца планета, тем слабее сила. Из сравнения двух планет на разных расстояниях следует, что силы обратно пропорциональны квадратам относительных расстояний. Сочетая оба закона, Ньютон пришел к заключению, что должна существовать сила, обратная квадрату расстояния и направленная по прямой между Солнцем и планетой.
Будучи человеком, склонным к обобщениям, Ньютон, конечно, предположил, что эта связь применима не только к Солнцу, удерживающему планеты, но что она носит более общий характер. Уже было известно, к примеру, что вокруг Юпитера обращаются луны, подобно тому как Луна ходит вокруг Земли, и Ньютону казалось естественным, что и планеты силой держат свои луны возле себя. Тогда он уже знал о силе, удерживающей
Тогда он спросил себя: притягивает ли Земля людей так же, как Луну («так же» значит обратно пропорционально квадрату расстояния). Если тело у поверхности Земли падает в первую секунду (из состояния покоя) на 4,9
Мысль, что Луна «падает», несколько смущает; почему же она тогда
Рассмотрим другой, уже чисто земной пример. Тело, выпущенное из рук у земной поверхности, упадет в первую секунду на 4,9
На фиг. 7.3 показан прибор, демонстрирующий это явление.
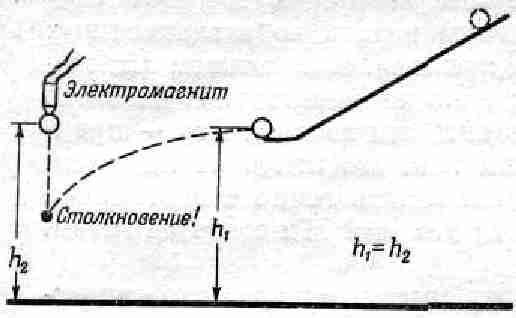 |
Фиг. 7.3. Прибор для демонстрации независимости вертикальных и горизонтальных движений.
Из горизонтального желоба выскакивает и летит вперед шарик. С той же высоты вертикально падает вниз другой шарик (имеется электрическая схема, выпускающая второй шар как раз в тот момент, когда первый соскальзывает с желоба). Они сталкиваются в воздухе, т. е. это значит, что они за одинаковое время снижаются одинаково. Пуля, выпущенная горизонтально, может пройти за 1
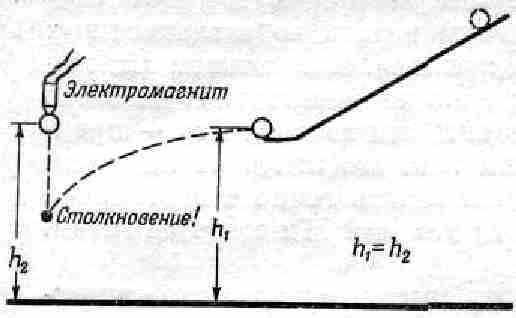 |
Остается вспомнить одну из занятных геометрических теорем о том, что длина полухорды, перпендикулярной диаметру, равна среднему геометрическому между длинами отрезков диаметра. Значит, расстояние, пройденное пулей, есть среднее пропорциональное между 4,9
0,049?12740?7,9
Итак, если пуля движется с быстротой 7,9
Любое открытие нового закона полезно лишь тогда, когда из него можно извлечь больше того, что в него было вложено. Ньютон
Закон тяготения объяснил многие явления, прежде непонятные. Например, притяжение Луны вызывает на Земле приливы – явление дотоле таинственное. Люди и раньше догадывались, что Луна притягивает воду под собой и получается прилив, но они не были так умны, как Ньютон, и думали, что должен быть только один прилив в сутки. Считалось, что Луна притягивает воду, вызывая прилив, но так как Земля вращается, то в каждом месте вода должна раз в сутки подняться и опуститься. А на самом деле прилив бывает каждые 12 часов. Была и другая школа передовой мысли; по ее мнению, прилив должен быть и на противоположной стороне Земли, потому что Луна всегда отрывает сушу от воды! Обе эти теории неверны. Настоящее объяснение примерно таково: притяжение Луной суши и воды «уравновешено» в центре. Но притяжение Луной тех масс воды, которые находятся на «лунной» стороне Земли,
Что мы понимаем под словом «уравновешено»? Что именно уравновешивается? А вот что. Если Луна притягивает к себе всю Землю, то почему Земля не падает «вверх» на Луну? По той же причине, почему и Луна не падает на Землю: Земля вращается вокруг точки, которая находится внутри Земли (но не в ее центре). Не Луна вращается вокруг Земли, а обе они вращаются вокруг общего центра и обе падают на него, как показано на фиг. 7.5.
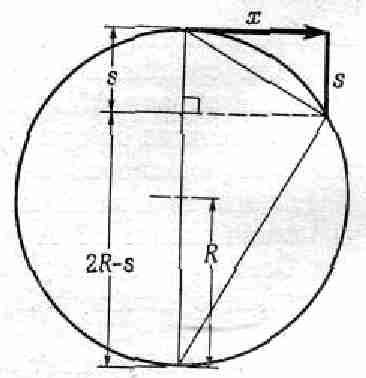 |
Фиг. 7.5. Система Земля–Луна с приливами.
Это движение вокруг общего центра и уравновешивает падение каждого из двух небесных тел. Так что и Земля тоже движется не по прямой линии, а по круговой орбите. Массы воды на дальней стороне отбрасываются из–за «центробежной силы» сильнее, чем центр Земли, который как раз уравновешен притяжением Луны. Притяжение Луны на дальней стороне слабее и «центробежная сила» больше. В итоге равновесие воды нарушается: она удаляется от центра Земли. На ближней стороне Луна притягивает сильнее, но из–за меньшей величины радиус–вектора оказывается меньше и «центробежная сила», равновесие нарушается в обратную сторону, но по–прежнему
$ 5. Всемирное тяготение
Что же еще можно понять, зная о существовании тяготения? Всем известно, что Земля круглая. А почему? Ну, это понятно: конечно, благодаря тяготению. Земля круглая просто потому, что между всеми телами существует притяжение, и все, из чего возникла Земля, тоже взаимно притягивалось до тех пор, пока было куда притягиваться! Точнее говоря, Земля
Что же еще следует из закона тяготения? Наблюдая за спутниками Юпитера, можно понять все законы их движения вокруг планеты. В этой связи стоит рассказать об одной заминке, которая вышла у закона тяготения с лунами Юпитера. Эти спутники очень подробно изучались Рёмером, и вот он заметил, что временами они нарушают расписание: то опаздывают, то приходят в назначенное место раньше времени (расписание можно составить, понаблюдав за ними достаточно долго и подсчитав по многим оборотам средний период обращения). Более того, он заметил, что опоздания случаются, когда Юпитер удален от Земли, а когда мы от Юпитера близко, то движение лун опережает расписание. Такую вещь очень трудно было уложить в закон тяготения, и ему бы угрожала безвременная кончина, не найдись другого объяснения. Ведь если закону противоречит хотя бы один случай, то закон неверен. Но причина расхождения оказалась очень естественной и красивой: дело просто в том, что необходимо какое–то время, чтобы увидеть луну на нужном месте, ведь свет от нее до нас доходит не мгновенно. Время это небольшое, когда Юпитер находится близко к Земле, но оно затягивается, когда Юпитер удалится от нее. Вот почему кажется, что луны в среднем торопятся или отстают в зависимости от того, близко ли или далеко они находятся от Земли. Это явление доказало, что свет распространяется не мгновенно, и снабдило нас первой оценкой его скорости (было это в 1676 г.).
Если все планеты притягиваются друг к другу, то сила, управляющая, скажем, обращением Юпитера вокруг Солнца, это не совсем сила притяжения к Солнцу; ведь есть еще и притяжение, например, Сатурна. Оно невелико (Солнце куда больше Сатурна), но оно
Это открытие показывает, что в солнечной системе законы Ньютона абсолютно верны. Но верны ли они на расстояниях, больших, чем относительно малые расстояния до планет? Во–первых, можно поставить вопрос: притягивают ли
 |
Сравнивая с «фиксированной» звездой, мы видим, что ось пары повернулась, т. е. звезды ходят одна вокруг другой. Вращаются ли они в согласии с законами Ньютона? Тщательные замеры относительной позиции двойной звезды Сириус даны на фиг. 7.7.
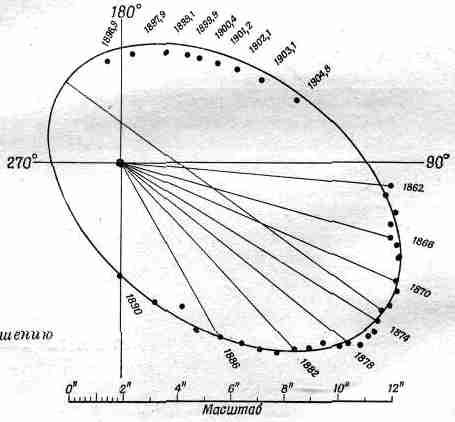 |
Получается превосходный эллипс (измерения начаты в 1862 г. и доведены до 1904 г.; с тех пор был сделан еще один оборот). Все сходится с законами Ньютона, кроме того, что Сириус А получается
Справедливость закона тяготения на больших дистанциях видна из фиг. 7.8.
 |
Фиг. 7.8. Шаровое звездное скопление.
Нужно быть лишенным воображения, чтобы не увидеть здесь работы тяготения. Здесь показано одно из красивейших небесных зрелищ – шаровое звездное скопление. Каждая точка – это звезда. Нам кажется, будто у центра они набиты вплотную; происходит это из–за слабой чувствительности телескопа; на самом деле промежутки между звездами даже в середине очень велики, а столкновения крайне редки. Больше всего звезд в центре, а по мере удаления к краю их все меньше и меньше. Ясно, что между звездами действует притяжение, т. е. что тяготение существует и на таких гигантских расстояниях (порядка 100 000 диаметров солнечной системы).
Но отправимся дальше и рассмотрим
 |
Фиг. 7.9. Галактика.
Форма ее явственно указывает на стремление ее вещества стянуться. Конечно, доказать, что здесь действует закон обратных квадратов, нельзя; видно только, что и на таком протяжении есть силы, удерживающие всю галактику от развала. Вы можете сказать: «Ладно, все это разумно, но почему же эта штука, галактика, уже не похожа на шар?» Да потому, что она
Но тяготение проявляется и на больших протяжениях. На фиг. 7.10 показаны какие–то скопления мелких пятен.
 |
Фиг. 7.10. Облако галактик.
Это
Закон тяготения ведет не только к пониманию природы туманностей, но и к некоторым идеям о происхождении звезд. В большом облаке пыли и газа, подобном изображенному на фиг. 7.11, притяжение частиц пыли соберет их в комки.
 |
На фигуре видны «маленькие» черные пятнышки – быть может, начало скопления газа и пыли, из которых благодаря их притяжению начинает возникать звезда. Приходилось ли нам когда–либо видеть рождение звезды – вопрос спорный. На фиг. 7.12 дано некоторое свидетельство того, что приходилось.
 |
Слева показан светящийся газ, а внутри него – несколько звезд. Это снимок 1947 г. Снимок справа сделан через 7 лет; теперь видны уже два новых ярких пятна. Уж не скопился ли здесь газ, не вынудило ли его тяготение собраться в шар, достаточно большой, чтобы в нем началась звездная ядерная реакция, превращая его в звезду? Может быть, да, а может, и нет. Маловероятно, что нам повезло увидеть, как всего за семь лет звезда стала видимой, но еще менее вероятно увидать рождение сразу
§ 6. Опыт Кавендиша
Итак, тяготение распространяется на огромные расстояния. Но если существует притяжение между
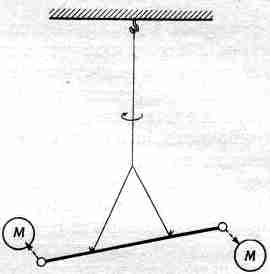 |
Опыт Кавендиша доказал, что существует сила, действующая между двумя большими закрепленными свинцовыми шарами и двумя меньшими (тоже из свинца); в опыте шары размещались на концах коромысла, висящего на очень тонкой упругой нити. Измеряя, насколько закрутится нить, можно было узнать величину силы и убедиться, что она обратно пропорциональна квадрату расстояния. Таким образом точно определялся коэффициент G в формуле
F=Gmm'r2
ибо все массы и расстояния здесь известны. Вы можете возразить: «Все это для Земли было известно и раньше». Все, кроме
6,670?10–11 ньютон?м2/кг2
Трудно преувеличить силу влияния теории тяготения, ее величественных успехов на историю науки. Вместо царивших в прежние века неуверенности, сомнений, неполноты знаний, бесконечных споров и парадоксов перед людьми предстал новый закон во всей своей четкости и простоте. Как важно было то, что все луны, все планеты, все звезды подчиняются столь
§ 7. Что такое тяготение?
Но почему закон так прост? Что можно сказать о причине этого? До сих пор мы только описывали,
Предлагались многие механизмы тяготения. Интересно рассмотреть один из них, ибо до него время от времени додумывались то один, то другой ученый. Причем каждый сперва воспрянет духом и ходит осчастливленный своим «открытием», но потом начинает понимать, что тут что–то не так. Впервые это открытие произошло примерно в 1750 г. Представьте себе, что в пространстве носится в разных направлениях с огромной скоростью множество частиц, лишь слегка поглощаемых веществом. Поглощаясь, они передают свой импульс Земле. Но так как во всех направлениях их количество одинаково, то все импульсы уравновешиваются. Когда же неподалеку находится Солнце, то частицы, приближающиеся к Земле сквозь Солнце, частично им поглощаются, так что от Солнца их проходит меньше, чем с обратной стороны. Следовательно, Земля ощутит импульс, направленный к Солнцу, и нетрудно видеть, что он будет обратным квадрату расстояния: таков закон изменения пространственного угла, под которым видимо Солнце, с ростом расстояния. Что же плохо в этом механизме? Неверны те выводы, которые из него следуют. Появляется новая забота: Земля в своем движении вокруг Солнца будет испытывать больше столкновений с частицами спереди, чем сзади (когда бежишь навстречу дождю, лицо мокнет больше, чем затылок!). Поэтому спереди Земля получит больше импульсов, чем сзади, и должна почувствовать
Рассмотрим еще возможную связь тяготения с прочими силами. В нынешнее время не удается свести тяготение к другим силам. Тяготение отнюдь не проявление электричества или чего–либо подобного; этим его не объяснишь. И все же тяготение похоже на другие силы, и любопытно посмотреть, в чем. К примеру, электрическая сила между двумя заряженными телами чрезвычайно похожа на тяготение: она равна со знаком минус постоянной величине, умноженной на величины зарядов тел, и изменяется обратно квадрату расстояния. Правда, она действует в обратную сторону, т. е. отталкивает. Но замечательно не столько это, сколько одинаковая зависимость от расстояния, входящая в оба закона. Не исключено, что тяготение и электричество связаны значительно сильнее, чем мы думаем. Было сделано много попыток объединить их; так называемая единая теория поля – лишь одна из очень изящных попыток сочетать электричество с тяготением. Но самая интересная вещь в сопоставлении их друг с другом – это
Если мы измерим в естественных единицах отталкивание двух электронов (возникающее из–за того, что у них есть заряд) и их притяжение (возникающее оттого, что у них есть масса), то мы можем получить и отношение электрического отталкивания к гравитационному притяжению. Отношение это не зависит от расстояния, это фундаментальная мировая константа. Изображена она на фиг. 7.14.
 |
Гравитационное притяжение составляет 1/4,17?1042 от электрического отталкивания! Откуда же может возникнуть такое исполинское число в знаменателе? Оно же не случайно, ведь это не отношение объема Земли к объему тли. Мы рассматриваем два естественных свойства одного и того же предмета – электрона. Это фантастическое число есть естественная константа, и в нем таятся какие–то глубинные свойства природы. От каких же свойств оно зависит? Некоторые надеются, что если кто–нибудь однажды напишет «универсальное уравнение», то одним из его корней будет это число. Но очень трудно найти уравнение, в котором корнем было бы такое немыслимое число. Были придуманы и другие возможности; одна связывает его с возрастом Вселенной. Иначе говоря, необходимо найти в природе
Как пример чего–то естественного выберем время, за какое свет проходит сквозь протон, 10–24
Вот один из способов проверить эту мысль. Зададим вопрос: что при этом должно было измениться за последние 109 лет (время появления жизни на Земле), т. е. за 110 возраста Вселенной? За это время постоянная тяготения выросла бы на 10%. Оказывается, что если рассмотреть структуру Солнца – баланс между его массой и степенью генерации излучательной энергии внутри Солнца, – то при росте тяжести на 10% Солнце оказалось бы не на 10% ярче, а значительно больше: яркость его возросла бы как
Как известно, сила тяготения пропорциональна массе, т. е. мере
Этвешем в 1909 г., а позже повторенном Дикке. У всех веществ масса и вес пропорциональны с точностью 1/1 000 000 000 или даже более того. Не правда ли, замечательный эксперимент?
§ 8. Тяготение и относительность
Заслуживает еще обсуждения видоизменение ньютонова закона тяготения, сделанное Эйнштейном. Оказывается, несмотря на вызванное им воодушевление, ньютонов закон тяготения все же неверен! Учтя требования теории относительности, Эйнштейн видоизменил этот закон. Согласно Ньютону, тяготение действовало мгновенно. Это значит вот что: сдвинув массу, мы должны в тот же миг почувствовать изменение силы в результате смещения; стало быть, таким способом можно посылать сигналы с бесконечной скоростью. А Эйнштейн выдвинул доводы, что
И наконец, сопоставим тяготение с другими теориями. В последние годы выяснилось, что любая масса обязана своим происхождением мельчайшим частицам и что существует несколько видов взаимодействия, например ядерные силы и т. п. Ни одна из этих ядерных или электрических сил пока тяготения не объясняет. Квантовомеханические стороны природы мы еще пока не распространили на тяготение. Когда на малых расстояниях начинаются квантовые эффекты, то тяготение оказывается еще настолько слабым, что нужды в квантовой теории тяготения не возникает. С другой стороны, для последовательности наших физических теорий было бы важно понять, должен ли закон Ньютона с внесенным Эйнштейном видоизменением быть изменен и дальше с тем, чтобы согласовываться с принципом неопределенности. Это последнее видоизменение пока не сделано.
* Иначе говоря, на сколько окружность (орбита Луны) отходит от касательной к ней на протяжении пути, проходимого Луной за 1 сек.
Глава 8 ДВИЖЕНИЕ
§ 1. Описание движения
Чтобы найти законы, управляющие различными изменениями, происходящими с течением времени, нужно сначала
На первый взгляд это кажется совсем просто, однако в описании изменения есть много хитростей. Некоторые изменения описать труднее, нежели движение точки на твердом предмете. Например, как описать движение облака, которое не только медленно перемещается, но вдобавок еще изменяет свои очертания или испаряется? Или как описать капризы женского ума? Впрочем, поскольку изменения облака хотя бы в принципе можно описать с помощью движения всех отдельных молекул его составляющих, то вполне возможно, что и изменения мыслей обусловлены тоже какими–то перемещениями атомов в мозгу, хотя мы еще не знаем простого способа их описания.
По этой причине мы начнем с движения точек. Пожалуй, еще можно считать эти точки атомами, но сначала, вероятно, лучше не гнаться за точностью, а просто представлять себе точку как какой–то маленький объект, маленький по сравнению с тем расстоянием, которое он проходит. Например, если говорят об автомобиле, прошедшем 100
Таблица 8.1 расписание движения автомобиля
 |
Через минуту после начала движения он проходит уже 380
Это один способ описать движение. Есть и другой способ – графический. Если по горизонтали откладывать время, а по вертикали – расстояние, то получим кривую, подобную изображенной на фиг. 8.1.
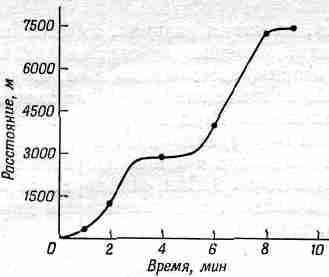 |
Из рисунка видно, что с увеличением времени расстояние тоже увеличивается, сначала очень медленно, а затем все быстрее и быстрее. В районе четырех минут происходит замедление, а затем расстояние опять увеличивается в течение нескольких минут, и, наконец, на девятой минуте машина останавливается. Все эти сведения можно получить прямо из графика, не используя таблицы. Конечно, для построения нашего графика необходимо знать, где находится автомобиль не только каждую минуту, но и каждые полминуты, а может быть, и еще точнее. Кроме того, мы предполагаем, что машина где–то находится в любой момент времени.
Так что движение автомобиля выглядит все же сложно. Давайте рассмотрим что–нибудь попроще, с более простым законом движения: например, падающий шар. В табл. 8.2 даны значения времени в секундах и расстояния в метрах.
Таблица 8.2 расписание движения падающего шара
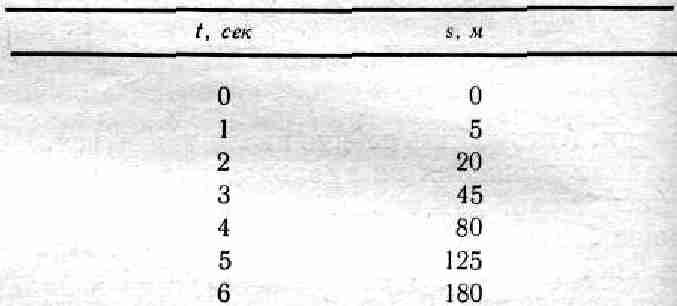 |
За нулевой момент выберем момент начала падения. Через 1
s=5t2
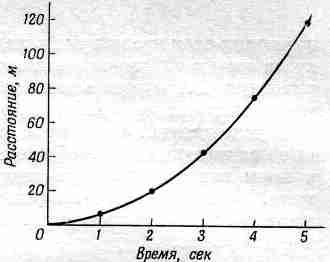 |
Фиг. 8.2. График зависимости расстояния, пройденного падающим шаром, от времени.
Эта формула позволяет вычислить расстояние для любого момента времени. Вы скажете, что для первого графика (см.фиг. 8.1) тоже должна быть какая–то формула. Действительно это так. Ее можно записать в таком абстрактном виде:
Это означает, что s – величина, зависящая от
На этих двух примерах видно, что любое движение можно описать в общей и простой форме. Казалось бы, нет ничего хитрого! Однако хитрости все же есть, и не одна! Во–первых, что мы понимаем под
Другая хитрость (мы уже упоминали о ней) – это правильно ли думать, что наблюдаемая нами движущаяся точка всегда находится в каком–то определенном месте (т. е. где–то локализована). Разумеется, когда мы смотрим на нее, она находится в определенном месте; но можно ли это утверждать в те моменты, когда мы отвернулись. И вот оказывается, что при изучении движения атомов так думать нельзя. Невозможно посадить метку на атом и наблюдать за его движением. С этой тонкостью мы вплотную столкнемся в квантовой механике. Но сначала давайте рассмотрим те проблемы, которые возникают до введения этих усложнений, а уж после этого учтем те поправки, на которые нас вынуждают новейшие сведения о природе вещей. Итак, примем наиболее простую точку зрения о пространстве и времени. Мы приблизительно понимаем, что означают эти понятия, а тот, кому доводилось управлять автомобилем, знает и что такое скорость.
§ 2. Скорость
Хотя мы примерно представляем себе, что такое «скорость», однако здесь есть одна очень важная тонкость. Заметьте, что древние греки так и не смогли до конца разобраться в проблеме скорости. Тонкость, о которой идет речь, дает себя знать, когда пытаешься точно определить, что же подразумевается под понятием «скорость». Этот вопрос был камнем преткновения для древних греков, и потребовалось открытие новой области математики, помимо геометрии и алгебры, которые были известны и грекам, и арабам, и вавилонянам. Попробуйте–ка с помощью одной лишь алгебры решить следующую задачу. Воздушный шар надувается таким образом, что его объем увеличивается со скоростью 100
Чтобы еще яснее представить себе эти трудности, вспомним старую шутку, которую вы наверняка слышали. Вы помните, что автомобиль, о котором мы говорили в начале этой лекции, был остановлен полицейским. Он подходит к машине и говорит: «Мадам (ибо за рулем была женщина), Вы нарушили правила уличного движения. Вы ехали со скоростью 90 километров в час». Женщина отвечает: «Простите, это невозможно. Как я могла делать 90 километров в час, если я еду всего лишь 7 минут!» Как бы вы ответили на месте полицейского? Конечно, если вы действительно настоящий полицейский, то такими хитростями вас не запутаешь. Вы бы твердо сказали: «Мадам, оправдываться будете перед судьей!» Но предположим, что у вас нет такого выхода. Вы хотите честно доказать нарушительнице ее вину и пытаетесь объяснить ей, что означает скорость 90
Аналогичная проблема возникает и в случае падающего шарика. Предположим, что мы хотим определить его скорость через 3 сек, если бы он двигался таким же образом. Но что означает «двигался таким же образом»? Сохранял бы ускорение, двигался быстрее, что ли? Конечно, нет! Сохранял бы ту же самую
Многие физики думают, что единственным определением любого понятия является способ его измерения. Но тогда при объяснении вы должны прибегнуть к прибору, измеряющему скорость. «Смотрите, – скажете вы в этом случае, – ваш спидометр показывает 60». «Мой спидометр сломан и давно не работает», – ответит она. Но достаточно ли этого, чтобы поверить, что машина не двигалась? Мы полагаем, что как–то нужно было бы определять скорость и без помощи спидометра. Только при этих условиях можно сказать, что спидометр не работает, что он сломан. Это было бы абсурдным, если бы скорость не имела смысла без спидометра. Очевидно, что понятие «скорость» не зависит от спидометра. Спидометр нужен только для того, чтобы измерять ее. Давайте посмотрим, нельзя ли придумать лучшее определение понятия «скорость». Вы скажете: «Разумеется, мадам, если бы вы ехали таким же образом в течение часа, то налетели бы на стену, но за 1 секунду вы бы проехали 25 метров, так что вы делали 25 метров в секунду, и если бы продолжали ехать таким же образом, то в следующую секунду опять проехали бы 25 метров, а стена стоит гораздо дальше». «Но правила запрещают делать 90 километров в час, а не 25 метров в секунду». «Да ведь это то же самое, что и 90 километров в час», – ответите вы. А если это то же самое, то к чему тогда все длинные разговоры о 25
Но теперь мы, кажется, находимся на правильном пути, который приводит нас вот к чему. Если бы машина продолжала двигаться таким же образом следующую тысячную долю часа, то она прошла бы тысячную долю 90
Другими словами, можно определить скорость следующим образом. Определяем расстояние, которое было пройдено за очень малый отрезок времени, и, разделив его на этот отрезок времени, получаем скорость. Однако этот отрезок должен быть как можно меньше, и чем меньше, тем лучше, потому что в этот период могут произойти снова изменения. Смешно, например, для падающего тела в качестве такого отрезка принять час. Принять в качестве отрезка секунду, может быть, удобно для автомобиля, так как за секунду его скорость изменяется не слишком сильно, но этот отрезок велик для падающего тела. Таким образом, чтобы вычислить скорость более точно, нужно брать все меньшие и меньшие интервалы времени. Если на миллионную долю секунды мы разделим расстояние, которое было пройдено в течение этого времени, то получим расстояние в секунду, т.е. как раз то, что мы понимаем под скоростью. Именно это нужно было сказать нашей нарушительнице, т. е. дать то определение; скорости, которое мы и будем использовать.
Такое определение содержит некую новую идею, которая была недоступна грекам в ее общей форме.
Она заключается в том, чтобы
Попытаемся теперь точнее определить скорость. Пусть за некоторое малое время ? машина или какое–то другое тело прошли малое расстояние
v=x/?,
причем точность будет тем больше, чем меньше ?. Математики записывают это следующим образом:
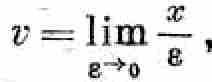 |
(8.3)
т. е. скорость есть предел отношения x/? при ?, стремящемся к нулю. Для нашей машины–нарушительницы невозможно точно вычислить скорость, так как таблица неполная. Ее положение известно нам только через интервалы 1
В качестве примера давайте найдем скорость падающего шара через 5
s=5?5,0012=5?25,010001=125,050005
Следовательно, в последнюю тысячную долю секунды шарик проходит 0,050005
v=x/?=10t0+5?. (8.4)
Теперь мы уже знаем, что нужно делать, чтобы получить скорость точно в момент t0
В нашей задаче t0=5
§ 3. Скорость как производная
Процедура, которую мы только что выполнили, настолько часто встречается в математике, что для величин ? и x: было придумано специальное обозначение: ? обозначается как ?t, а
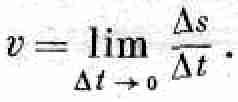 |
(8.5)
Это по существу формула (8.3), но теперь яснее видно, что здесь все изменяется, а, кроме того, она напоминает, какие именно величины изменяются.
Существует еще один закон, который выполняется с хорошей точностью. Он гласит: изменение расстояния равно скорости, умноженной на интервал времени, за которое это изменение произошло, т. е. ?s=v?t. Это правило строго справедливо только тогда, когда скорость не изменяется в течение интервала ?t, а это, вообще говоря, происходит, только когда ?t достаточно мало. В таких случаях обычно пишут
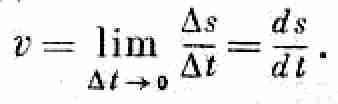 |
Величина
s+?s=A(t+?t)2+Bt+?t+C=At3+Bt+C+3At2?t+B?t+3At+3At(?t)2+A(?t)3
а
s=At3+Bt+C
то ?s=3At2?t+B?t+3At+3At(?t)2+A(?t)3.
Но нам нужна не сама величина ?s, а отношение ?s/?t. После деления на ?t получим выражение
?s/?t=3At2+B+3At?t+A(?t)2, которое после устремления ?t к нулю превратится в
?s/?t=3At2+B.
В этом состоит процесс взятия производной, или дифференцирования функций. На самом деле он несколько легче, чем это кажется на первый взгляд. Заметьте, что если в разложениях, подобных предыдущим, встречаются члены, пропорциональные (?t)2 или (?t)3 или еще более высоким степеням, то их можно сразу вычеркнуть, поскольку они все равно обратятся в нуль, когда в конце мы будем ?t устремлять к нулю. После небольшой тренировки вы сразу будете видеть, что нужно оставлять, а что сразу отбрасывать. Существует много правил и формул для дифференцирования различных видов функций. Их можно либо запомнить, либо пользоваться специальными таблицами. Небольшой список таких правил приводится в табл. 8,3.
Таблица 8.3 некоторые производные
 |
s, u,
§ 4. Расстояние как интеграл
Обсудим теперь обратную проблему. Пусть вместо таблицы расстояний нам дана таблица скоростей в различные моменты времени, начиная с нуля. В табл. 8.4 представлена зависимость скорости падающего шара от времени. Аналогичную таблицу можно составить и для машины, если записывать показания спидометра через каждую минуту или полминуты. Но можно ли, зная скорость машины в любой момент времени, вычислить расстояние, которое ею было пройдено?
Таблица 8.4 скорость падающего шара
 |
Эта задача обратна той, которую мы только что рассмотрели. Как же решить ее, если скорость машины непостоянна, если она то ускоряется до 90
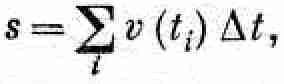 |
(8.6)
причем каждый последующий момент
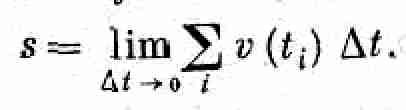 |
(8.7)
Математики придумали для этого предела, как и для дифференциала, специальный символ. Значок ? превращается в d, напоминая о том, что интервал времени сколь угодно мал, а знак суммирования превращается в ? – искаженное большое
s=?v(t)dt, (8.8)
где
Любая функция, заданная в аналитическом виде, т. е. выражающаяся через комбинацию известных нам функций, дифференцируется очень просто – вся операция выполняется чисто алгебраически, и в результате мы всегда получаем какую–то известную функцию. Однако интеграл не от всякой функции можно записать в аналитическом виде. Разумеется, для каждого частного интеграла всегда сначала пытаются найти такую функцию, которая, будучи продифференцирована, давала бы функцию, стоящую после знака интеграла (она называется подынтегральной). Однако это не всегда удается сделать. В таких случаях интеграл вычисляют просто суммированием, т. е. вычисляют суммы типа (8.6) со все меньшими и меньшими интервалами, пока не получат результат с достаточной точностью.
§ 5. Ускорение
Следующий шаг на пути к уравнениям движения – это введение величины, которая связана с
Таким образом, ускорение определяется как быстрота изменения скорости. Всем сказанным ранее мы уже достаточно подготовлены к тому, чтобы сразу записать ускорение в виде производной от скорости, точно так же как скорость записывается в виде производной от расстояния. Если теперь продифференцировать формулу v=9,8
a=dv/dt=9,8. (8.9)
(При дифференцировании этого выражения использовался результат, полученный нами раньше. Мы видели, что производная от
В качестве следующего примера найдем ускорение в той задаче, с которой мы уже имели дело при изучении скорости:
Для скорости
Так как ускорение – это производная скорости по времени, то для того, чтобы найти его значение, нужно продифференцировать эту формулу. Вспомним теперь одно из правил табл. 8.3, а именно что производная суммы равна сумме производных. Чтобы продифференцировать первый из этих членов, мы не будем проделывать всю длинную процедуру, которую делали раньше, а просто напомним, что такой квадратичный член встречался нам при дифференцировании функции 5t2, причем в результате коэффициент удваивался, a
Выведем еще две полезные формулы, которые получаются интегрированием. Если тело из состояния покоя движется с постоянным ускорением
а расстояние, пройденное им к этому моменту времени,
Заметим еще, что поскольку скорость – это
 |
Так что теперь мы знаем, как записывается вторая производная.
Существует, конечно, и обратная связь между ускорением и расстоянием, которая просто следует из того, что
Все предыдущее рассмотрение было посвящено движению в одном измерении, а теперь мы коротко остановимся на движении в пространстве трех измерений. Рассмотрим движение частицы
vx=dx/dt (8.11)
а вертикальная составляющая, или y–компонента, равна
vy=dy/dt (8.12)
В случае трех измерений необходимо еще добавить
vz=dz/dt. (8.13)
Как, зная компоненты скорости, определить полную скорость в направлении движения? Рассмотрим в двумерном случае два последовательных положения частицы, разделенных коротким интервалом времени ?t = t2–t1 и расстоянием ?s. Из фиг. 8.3 видно, что
 |
(Значок ? соответствует выражению «приблизительно равно».)
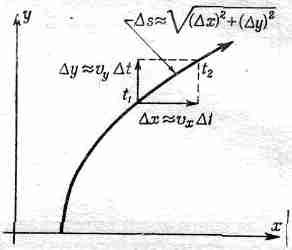 |
Фиг. 8.3. Описание движения тела на плоскости и вычисление его скорости.
Средняя скорость в течение интервала ?t получается простым делением: ?s/?t. Чтобы найти точную скорость в момент
 |
В трехмерном случае точно таким же способом можно получить
 |
Ускорения мы определяем таким же образом, как и скорости: x–компонента ускорения
Давайте рассмотрим еще один интересный пример смешанного движения на плоскости. Пусть шарик движется в горизонтальном направлении с постоянной скоростью u и в то же время падает вертикально вниз с постоянным ускорением
а поскольку ускорение движения вниз постоянно и равно–
Какую же кривую описывает наш шарик, т. е. какая связь между координатами x и y? Из уравнения (8.18), согласно (8.17), можно исключить время, поскольку
y=-(g/2u2)x2 (8.19)
Эту связь между координатами
 |
Так что любое свободно падающее тело, будучи брошенным в некотором направлении, движется по параболе.
Глава 9 ДИНАМИЧЕСКИЕ ЗАКОНЫ НЬЮТОНА
§ 1. Импульс и сила
Открытие законов динамики или законов движения стало одним из наиболее драматических моментов в истории науки. До Ньютона движение различных тел, например планет, представлялось загадкой для ученых, но после открытия Ньютона все вдруг сразу стало понятно. Смогли быть вычислены даже очень слабые отклонения от законов Кеплера, обусловленные влиянием других планет. Движение маятника, колебания груза, подвешенного на пружине, и другие непонятные до того явления раскрыли свои загадки благодаря законам Ньютона. То же самое можно сказать и об этой главе. До нее вы не могли рассчитать, как движется грузик, прикрепленный к пружине, не говоря уже о том, чтобы определить влияние Юпитера и Сатурна на движение Урана. Но после этой главы вам будет доступно и то и другое!
Первый большой шаг в понимании движения был сделан Галилеем, когда он открыл свой принцип инерции: тело, предоставленное самому себе, если на него не действует никакая сила, сохраняет свое прямолинейное движение с постоянной скоростью, как двигалось до этого, или остается в покое, если оно до этого покоилось. Конечно, в природе такого не бывает. Попробуйте толкнуть кубик, стоящий на столе. Он остановится. Причина в том, что кубик трется о стол, он не предоставлен самому себе. Нужно иметь очень богатое воображение, чтобы увидеть за этим принцип инерции.
Естественно нужно еще разрешить следующий вопрос: а как изменяется скорость тела, если на него что–то действует? Ответ был дан Ньютоном. Он сформулировал три закона. Первый закон представляет собой просто повторение принципа инерции Галилея. Второй закон говорит о том, как изменяется скорость тела, когда оно испытывает различные влияния, т. е. когда на него действуют силы. Третий закон в каком–то смысле описывает силы, но о нем мы поговорим несколько позже. Здесь будет идти речь о Втором законе, согласно которому под действием силы движение тел изменяется следующим образом: скорость изменения со временем некой величины, называемой количеством движения, или импульсом, пропорциональна силе. Позднее мы запишем короткую математическую формулировку этого закона, а сейчас давайте разберемся в его содержании.
Импульс и скорость – вещи разные. В физике употребляется много слов, и каждое из них в отличие от обычного разговорного языка имеет точный смысл. Примером может служить слово «импульс», и мы должны определить его точно. Толкните слегка рукой какой–нибудь легкий предмет – он тотчас начнет двигаться. Если с такой же силой толкнуть гораздо более тяжелый предмет, то он будет двигаться значительно медленней. В сущности нужно говорить не о «легком» или «тяжелом» предмете, а о менее массивном или более массивном, так как между весом и инерцией предмета есть разница, которую нужно понимать. (Сколько весит тело – это одно, а насколько трудно разогнать его – совсем другое.) Однако на поверхности Земли вес и инерция пропорциональны друг другу и зачастую рассматриваются как численно равные. Это часто приводит к непониманию разницы между ними. На Марсе, например, вес предметов будет отличаться от веса на Земле, но инертность останется той же самой, т. е. потребуется то же количество силы, чтобы преодолеть инерцию тела.
Количественной мерой инертности является масса. Ее можно измерять так: просто привязать предмет на веревочке, крутить его с определенной скоростью и измерять ту силу, которая необходима, чтобы удержать его. Этим способом можно измерять массу любых предметов. Импульс – это просто произведение массы тела на его скорость. Теперь можно записать Второй закон Ньютона в математической форме:
F =(d/dt)(mv). (9.1)
Давайте разберем подробнее некоторые его стороны. При написании закона, подобного этому, обычно используется много интуитивных идей; что–то подразумевается, что–то предполагается и комбинируется в приближенный «закон». Но после этого необходимо снова вернуться назад и подробно изучить, что означает каждый член. Если же пытаться сделать это с самого начала, то можно безнадежно запутаться. Так что мы считаем некоторые положения само собой разумеющимися и но требующими никакого доказательства. Во–первых, мы считаем, что массы тел постоянны. Это, вообще говоря, неправильно, но мы начнем с ньютоновского приближения, когда масса считается постоянной и не изменяющейся с течением времени. Во–вторых, если сложить вместе два предмета, то масса образовавшегося тела равна сумме их масс. Это положение неявно предполагалось Ньютоном, когда он писал свои уравнения, в противном случае они были бы бессмысленны. Пусть, например, масса изменяется обратно пропорционально скорости, но тогда импульс никогда бы не изменялся и закон потерял бы всякое содержание, за исключением только того, что вы знаете, как изменяется масса со скоростью. Так что сначала мы считаем массу неизменной.
Несколько слов о силе. В качестве первого грубого приближения мы рассматривали силу как некий толчок или тягу, которая может быть произведена с помощью наших мышц, но теперь, пользуясь уравнением движения, мы можем определить ее более точно. Очень важно помнить, что закон Ньютона включает не только изменение величины импульса, но и изменение его направления. Итак, если масса постоянна, то уравнение (9.1) можно записать в виде
F =m(dv/dt)=ma, (9.2)
где а – ускорение, т. е. «скорость изменения скорости». Второй закон Ньютона означает не только то, что изменения, вызванные данной силой, обратно пропорциональны массе, но и то, что направление изменения скорости совпадает с направлением действия силы. Важно понимать, что термин «ускорение» имеет в физике более широкий смысл, чем в обычной разговорной речи. Он означает не только увеличение скорости, но и замедление ( в этом случае мы говорим, что ускорение отрицательно), и перемену направления движения. В гл. 7 мы уже познакомились с ускорением, направленным под прямым углом к скорости, и мы видели, что предмет, движущийся по окружности радиусом R со скоростью v, за малый интервал времени t уклоняется от своего прямого пути на расстояние 1/2(v2/R)t2. Так что в этом случае ускорение направлено под прямым углом к направлению движения и равно
a =v2/R. (9.3)
Таким образом, сила, действующая под прямым углом к скорости, вызывает искривление пути, причем радиус кривизны можно найти, деля силу на массу тела (при этом мы получаем ускорение) и используя затем формулу (9.3).
Термин «скорость» тоже имеет в физике более широкий смысл, чем в обыденной жизни. Это не просто некоторое количество метров в секунду, т. е. абсолютная величина скорости, но и направление перемещения в каждый момент времени. Математически мы можем описать и величину, и направление скорости, если будем задавать изменение координат тела с течением времени. Пусть, например, в некоторый момент тело движется так, как это показано на фиг. 9.1.
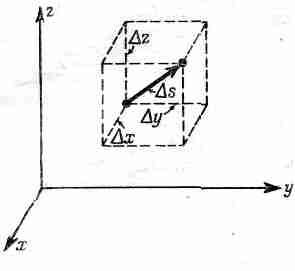 |
Фиг. 9.1. Малое перемещение тела.
Тогда за малый промежуток времени ?t оно пройдет некоторое расстояние ?х в направлении оси х, ?y в направлении оси у и ?z в направлении оси z. Результатом же этих изменений координат будет перемещение ?s вдоль диагонали параллелепипеда со сторонами ?x, ?y, ?z, которые следующим образом связаны с составляющими скорости и интервалом:
?x=vx?t, ?y=vy?t, ?z=vz?t. (9.4)
§ 2. Компоненты скорости, ускорения и силы
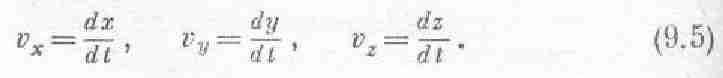 |
В уравнении (9.4) мы разложили скорость на составляющие (или компоненты), которые говорят нам, насколько быстро продвигается тело в направлениях х, у и z. Скорость будет полностью определена как в отношении ее направления, так и абсолютной величины, если задать числовые значения трех ее компонент:
При этом абсолютная величина равна
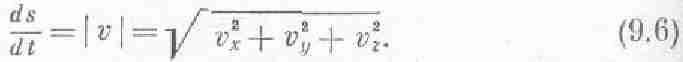 |
Теперь пусть под действием силы меняется не только величина, но и направление скорости (фиг. 9.2). Хотя это довольно сложный случай, но с помощью подсчета изменения компонент его рассмотрение сильно упрощается. Изменение x–компоненты скорости за интервал ?t будет ?vx=ax?t, где ах то, что называется x–компонентой ускорения. Совершенно аналогично ?vx =aу?t и Дvz=at?t. В такой формулировке Второй закон Ньютона фактически превращается в три закона. Действительно, мы говорим, что сила имеет то же направление, что и ускорение, так что каждая из составляющих силы в направлениях х, у и z равна массе, умноженной на изменение соответствующей компоненты скорости:
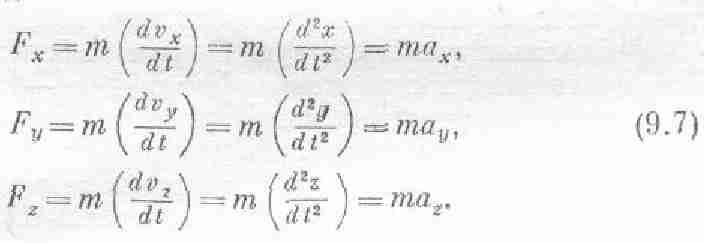 |
Подобно скорости и ускорению, сила тоже может быть разложена на компоненты, причем каждая из них является проекцией отрезка прямой, численно равного абсолютной величине силы и указывающего направление ее действия, на оси х, у и z:
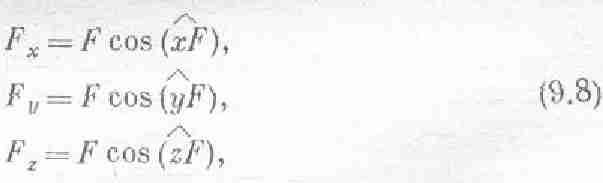 |
где F – абсолютная величина силы, a (xF), (yF) и (zF)– углы между направлением силы и осями х, у и z соответственно.
Уравнения (9.7) представляют собой полную форму Второго закона Ньютона. Зная силы, действующие на тело, и разлагая их на компоненты, можно с помощью этих уравнений найти движение тела. Давайте рассмотрим простой пример. Пусть в направлениях х и у не действуют никакие силы, а есть сила только в направлении z (скажем, вертикально). Тогда, согласно уравнению (9.7), изменяется только одна вертикальная составляющая скорости; что же касается горизонтальных, то они будут оставаться неизменными. Пример такого движения уже рассматривался в гл. 7 (см. фиг. 7.3). Таким образом, горизонтальное движение падающего тела остается неизменным, тогда как в вертикальном направлении оно движется так, как будто никакого горизонтального движения вообще нет. Другими словами, если компоненты сил не связаны друг с другом, то и движения в направлениях осей х, у и z будут независимы.
§ 3. Что такое сила?
Чтобы пользоваться законами Ньютона, мы должны иметь какую–то формулу для сил; ведь эти законы говорят нам: подумайте о силах. Если тело ускоряется, стало быть, на него что–то действует. А как найти это «что–то»? Нашей программой на будущее должно быть отыскание законов для сил. Некоторые из таких законов были найдены самим Ньютоном. Например, формула для силы тяготения. Часть сведений о силах другого рода содержится в Третьем законе, который утверждает равенство сил действия и противодействия, но об этом более подробно пойдет речь в следующей главе.
Продолжим наш предыдущий пример. Что за силы действуют на тело вблизи поверхности Земли? Это – сила тяжести, направленная вертикально вниз, пропорциональная массе тела и для высот, много меньших, чем радиус Земли R, почти не зависящая от высоты; она равна F=GmM/R2=mg, где g=GM/R2– так называемое ускорение силы тяжести. В горизонтальном направлении тело по–прежнему будет двигаться с постоянной скоростью, однако движение в вертикальном направлении более интересно. По Второму закону Ньютона
 |
После сокращения массы m получаем, что ускорение в направлении х постоянно и равно g. Это хорошо известное движение свободно падающего тела, которое описывается уравнениями
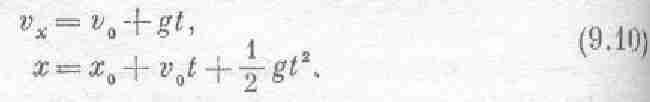 |
Рассмотрим другой пример. Представим, что мы смогли создать устройство (фиг. 9.3), в котором сила прямо пропорциональна отклонению от положения равновесия и направлена противоположно ему, – это пружина с грузиком.
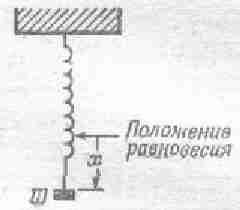 |
Действительно, поскольку сила тяжести компенсируется начальным натяжением пружины, то имеет смысл говорить только об избыточной силе. Если потянуть грузик вниз, то пружина растянется и потянет его вверх, если же толкать грузик вверх, то пружина сожмется и будет толкать его вниз. При этом все устроено таким образом, что чем больше сила и чем сильнее мы оттягиваем грузик вниз, тем больше растягивается пружина и тем сильнее она тянет его вверх, и наоборот. Наблюдая за работой этого устройства, мы видим довольно интересное движение: вверх – вниз, вверх – вниз… Возникает вопрос, могут ли уравнения Ньютона правильно описать его? Если применить закон Ньютона (9.7) для такого периодического осциллятора, то получим следующее уравнение:
 |
т. е. здесь мы встречаемся с таким положением, когда x–компонента скорости изменяется с быстротой, пропорциональной х. Нет смысла сейчас вводить многочисленные константы; в целях простоты предположим, что либо изменился масштаб времени, либо что–то произошло с другими единицами измерения, словом, они выбраны так, что klm равно единице. Итак, будем пытаться решать уравнение
 |
Чтобы пойти дальше, нужно сначала разобраться в том, что такое vx; то, что это быстрота изменения положения, нам, разумеется, уже известно.
§ 4. Смысл динамических уравнений
Попытаемся теперь понять, что же означает уравнение (9.12). Пусть в данный момент времени t тело находится в точке х и движется со скоростью vx. Каково будет его положение и скорость спустя небольшой промежуток времени, т. е. в момент t+?? Если мы сможем ответить на этот вопрос, то проблема решена, так как, исходя из начальных условий, т. е. положения и скорости в некоторый начальный момент времени, можно сказать, как они изменяются в первый момент, а зная положение и скорость в первый момент, можно найти их и в следующий и т. д. Таким образом, шаг за шагом выстраивается вся картина движения. Для большей определенности предположим, что в момент t=0 положение грузика х=1, а его скорость vx=0. Почему вообще движется грузик? Да потому, что на него в любом положении, за исключением положения равновесия х=0, действует сила. Если хgt;0, то эта сила направлена вверх. Следовательно, скорость, которая вначале была нулем, благодаря уравнениям движения начинает изменяться. Но как только скорость начинает возрастать, грузик приходит в движение. Для любого момента времени t при очень малом е можно с достаточно хорошей точностью найти положение в момент t+е через скорость и положение в момент t:
x(t+?)=x(t)+ ?vx(t). (9.13)
Конечно, это выражение тем точнее, чем меньше ?, но оно может быть достаточно точным, даже когда интервал ? не исчезающе мал. Что теперь можно сказать о скорости? Чтобы определить скорость в момент t+?, очевидно, нужно знать, как она изменяется со временем, т. е. нужно знать ускорение. А как узнать его? Вот здесь–то нам на помощь приходят уравнения динамики. Именно они позволяют определить, чему равно ускорение. В нашей задаче уравнение динамики говорит, что ускорение равно–x. Поэтому
vx(t+?)=vx(t)+ ?ax(t), (9.14)
= vx(t)- ?x(t). (9.15)
Уравнение (9.14) еще кинематическое; оно просто говорит о том, что из–за наличия ускорения скорость изменяется. Однако уравнение (9.15) уже динамическое, потому что оно связывает ускорение с силой. Оно говорит, что в данной частной задаче для данного момента времени ускорение можно заменить на–х(t). Следовательно, если в какой–то момент времени нам известны положение х и скорость vx, то мы знаем и ускорение, которое дает возможность найти скорость в следующий момент, а скорость в свою очередь определяет новое положение и т. д. Вот каким образом действует весь этот динамический механизм! Действующая сила немного изменяет скорость, а скорость приводит к небольшому изменению положения.
§ 5. Численнов решение уравнений
Давайте теперь действительно решим нашу задачу. Допустим, что мы взяли ?=0,100 сек. (Если после того, как мы проделаем все вычисления, окажется, что этот интервал не достаточно мал, то необходимо повторить все сначала с меньшим интервалом времени, например 0,010 сек.) Чему будет равно х(0,1), если в начальный момент времени х (0) = 1? Оно равно старому положению х(0) плюс скорость в начальный момент (которая равна нулю), умноженная на 0,10 сек. Таким образом, х(0,1) равно 1,00, ибо грузик еще не начал двигаться. Но новая скорость в момент 0,10 сек будет равна старой скорости v (0)=0 плюс ?, умноженное на ускорение. А само ускорение равно–х(0)=-1,00. Так что
v(0,1)=0,00+0,10•1,00=-0,10. В момент 0,20 сек
х(0,2)=х(0,1)+?v(0,1)=1,00–0,10•0,10=0,99
и
v(0,2)=v(0,1)+ ?a(0,1) =-0,10–0,10•1,00 =-0,20.
Продолжая эту процедуру еще и еще, можно найти положение и скорость в любой момент времени, а это как раз то, что нам нужно. Однако практически мы используем нехитрый прием, который позволит увеличить точность вычислений. Если бы мы продолжали начатые нами расчеты, то они оказались бы довольно грубыми, поскольку интервал ?=0,10 сек довольно большой. Пришлось бы уменьшить его, скажем, до 0,01 сек. Но тогда, чтобы проследить движение за какой–то разумный отрезок времени, потребовалось бы сделать множество шагов. Мы же организуем процесс таким образом, что сможем увеличить точность, используя тот же интервал ?=0,10 сек. Этого можно достичь, несколько изменив метод расчета.
Заметьте, что новое положение тела равно старому плюс интервал времени ?, умноженный на скорость. Но что это за скорость? В какой момент? В начале интервала одна скорость, а в конце она совсем другая. Прием состоит в том, чтобы брать скорость в середине интервала. Если известна скорость в настоящий момент и известно, что она меняется, как же можно надеяться получить удовлетворительный результат, считая, что тело все время движется с той же скоростью, что и в настоящий момент? Более разумно использовать какую–то среднюю скорость между началом и концом интервала. Те же рассуждения применимы к изменению самой скорости: для подсчета ее изменений нужно использовать ускорение в средней точке между двумя моментами времени, в которых необходимо найти скорость. Таким образом, реально мы будем пользоваться следующими уравнениями: положение в конце интервала равно положению в начале плюс интервал ?, умноженный на скорость в середине интервала. Эта скорость в свою очередь равна скорости в середине предыдущего интервала (т. е. на отрезок ? меньше) плюс ускорение в начале интервала, умноженное на ?.
Таким образом, мы будем пользоваться уравнениями
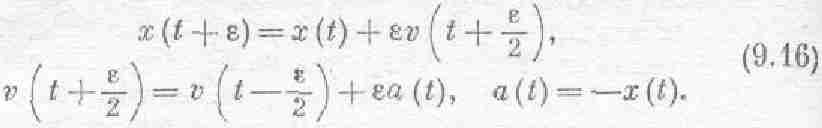 |
Остается еще один небольшой вопрос: что такое v (?/2)? Вначале у нас было v (0), а не v (-?/2). Но теперь, чтобы начать наши вычисления, необходимо использовать дополнительное уравнение v(?/2)=v (0)+( ?/2)а(0).
Таблица 9.1 • решение уравнения (dvx/dt)=-x Интервал ?=0,10 сек
 |
Ну, а теперь все готово для расчетов. Для удобства можно их выполнить в виде таблицы, в столбцах которой стоят время, положение, скорость и ускорение, причем скорость пишется в промежутках между строками (табл. 9.1). Такая таблица есть, конечно, просто удобный способ записи результатов, полученных из уравнений (9.16), и фактически полностью заменяет их. Мы просто заполняем одно за другим свободные места в ней и получаем очень интересную картину движения: сначала грузик находится в покое, затем понемногу приобретает отрицательную скорость (вверх), а это приводит к уменьшению его расстояния от точки равновесия. При этом хотя ускорение и становится меньше, оно все еще «подгоняет» скорость. Однако по мере приближения к положению равновесия (х=0) ускорение становится все меньше и меньше, скорость нарастает все медленней и медленней, но все же еще нарастает вплоть до точки x=0, которая достигается примерно через 1,5 сек. Скажем по секрету, что произойдет дальше. Грузик, конечно, не остановится в точке х=0, а пойдет дальше, но теперь все пойдет наоборот: его положение х станет отрицательным, а ускорение – положительным. Скорость начнет уменьшаться. Интересно сравнить полученные нами числа с функцией cost. Результат этого сравнения представлен на фиг. 9.4.
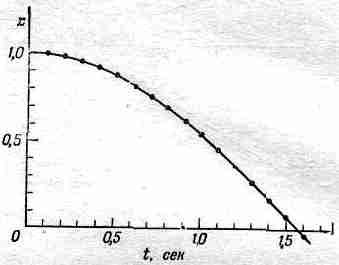 |
Оказывается, что в пределах точности наших расчетов (три знака после запятой) совпадение полное! Позднее вы узнаете, что функция cos t – точное решение нашего уравнения, так что у вас теперь есть наглядное представление о мощи численного анализа: столь простой расчет дает столь точный результат.
§ 6. Движение планет
Приведенный анализ очень подходит к движению осциллирующей пружинки с грузиком, но можно ли таким же путем вычислять движение планеты вокруг Солнца? Давайте посмотрим, можно ли при некоторых приближениях получить эллиптическую орбиту. Предположим, что Солнце бесконечно тяжелое в том смысле, что его движение не будет приниматься в расчет.
Допустим, что в известной точке планета начала свое движение и имеет определенную скорость. Она движется вокруг Солнца по какой–то кривой, и мы попытаемся определить с помощью уравнений движения Ньютона и его же закона всемирного тяготения, что это за кривая. Как это сделать? В некоторый момент времени планета находится в каком–то определенном месте, на расстоянии r от Солнца; в этом случае известно, что на нее действует сила, направленная по прямой к Солнцу, которая, согласно закону тяготения, равна определенной постоянной, умноженной на произведение масс планеты и Солнца и деленной на квадрат расстояния между ними. Чтобы рассуждать дальше, нужно выяснить, какое ускорение вызывает эта сила.
Однако в отличие от предыдущей задачи нам потребуются теперь компоненты ускорения в двух направлениях, которые мы назовем х и у. Положение планеты в данный момент будет определяться координатами х и у, поскольку третья координата z всегда равна нулю.
Действительно, координатная плоскость ху выбрана нами таким образом, что z–компоненты как силы, так и начальной скорости равны нулю, а поэтому нет никаких причин, которые бы заставили планету выйти из этой плоскости. Сила при этом будет направлена по линии, соединяющей планету с Солнцем, как это показано на фиг. 9.5.
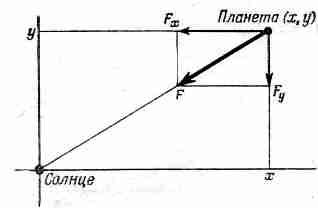 |
Из этого рисунка видно, что горизонтальная компонента силы так относится к полной ее величине, как координата х относится к расстоянию r. Это сразу следует из подобия треугольников. Кроме того, если х положительна, то Fx отрицательна, и наоборот.
Таким образом, Fx?F?=-x/r, или Fя=-?F?xlr=-GM mx/r3 и соответственно Fy=-GMmy/r3. Теперь можно воспользоваться динамическими законами (9.7) и написать, что х–или y–компонента ускорения, умноженная на массу планеты, равна соответственно х–или y–компоненте силы:
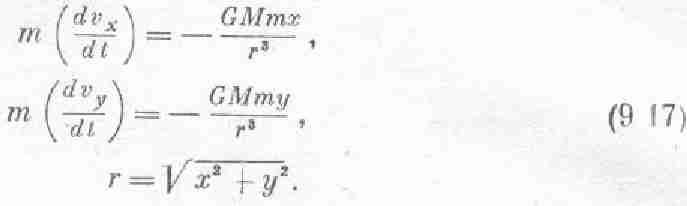 |
Это именно та система уравнений, которую мы должны решить. Для того чтобы упростить вычисления, предположим, что либо единицы измерения времени или массы выбраны соответствующим образом, либо нам просто повезло, словом, получилось так, что GM=1. Для нашего случая предположим, что в начальный момент t=0 планета находилась в точке с координатами х=0,500 и у=0,000, а скорость ее в этот момент направлена параллельно оси у и равна 1,6300. Как же в этом случае делаются расчеты? Снова составляется таблица со столбцами для времени t, координаты х, x–компонент скорости vx и ускорения ах. Затем идут отделенные чертой три колонки: для координаты y, у–компонент скорости и ускорения. Однако, для того чтобы подсчитать ускорения, мы должны воспользоваться уравнением (9.17), согласно которому его компоненты равны –х/r3 и –у/r3, а r=?(x2+y2). Так что, получив х и у, мы должны где–то в сторонке провести небольшие вычисления – извлечь квадратный корень из суммы квадратов и получить расстояние. Удобно также отдельно вычислить и 1/r3.
После этого все готово, чтобы определить компоненты ускорения. Всю эту работу можно сильно облегчить, если пользоваться таблицами квадратов, кубов и обратных величин. На нашу долю останется тогда только умножение х на 1/r3, которое легко выполняется на логарифмической линейке.
Перейдем к дальнейшему. Возьмем интервал времени ?=0,100. В начальный момент t=0
x(0)=0,500,. у(0)=0,000,
vx(0) = 0,000, vy(0)=+1,630.
Отсюда находим
r(0)=0,500, 1/r3=8,000,
ax=-4,000, ау=0,000.
После этого можно вычислять компоненты vx (0,05) и vy (0,05):
vя (0,05)=0,000–4,000•0,050 = -0,200,
vy(0,05)=1,630+0,000–0,100=1,630.
А теперь начнем наш основной расчет:
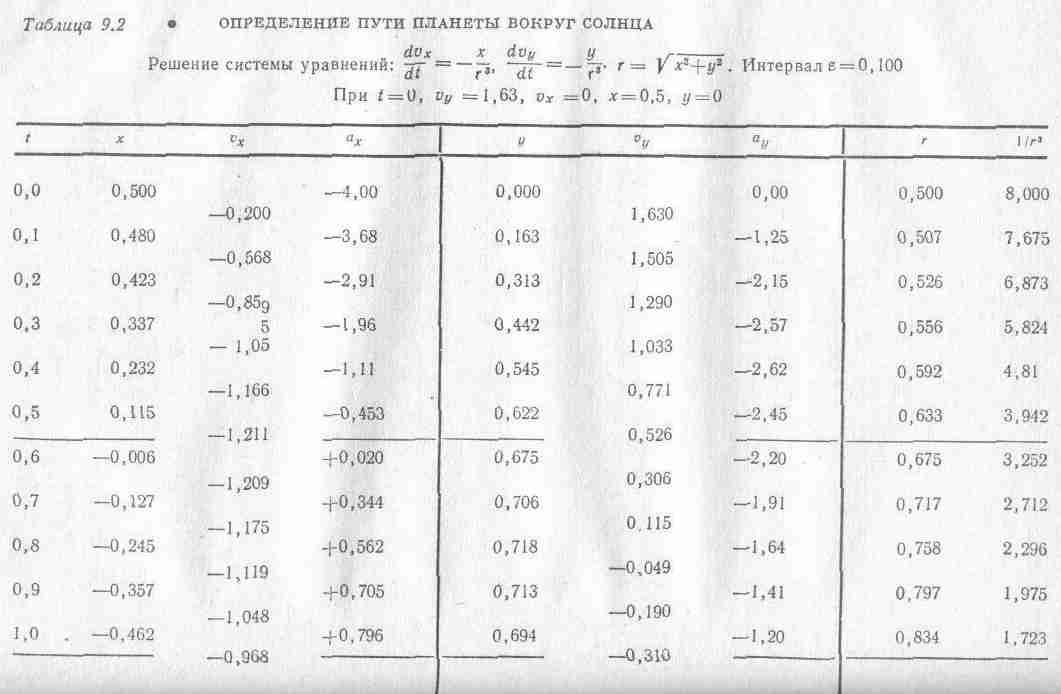 |
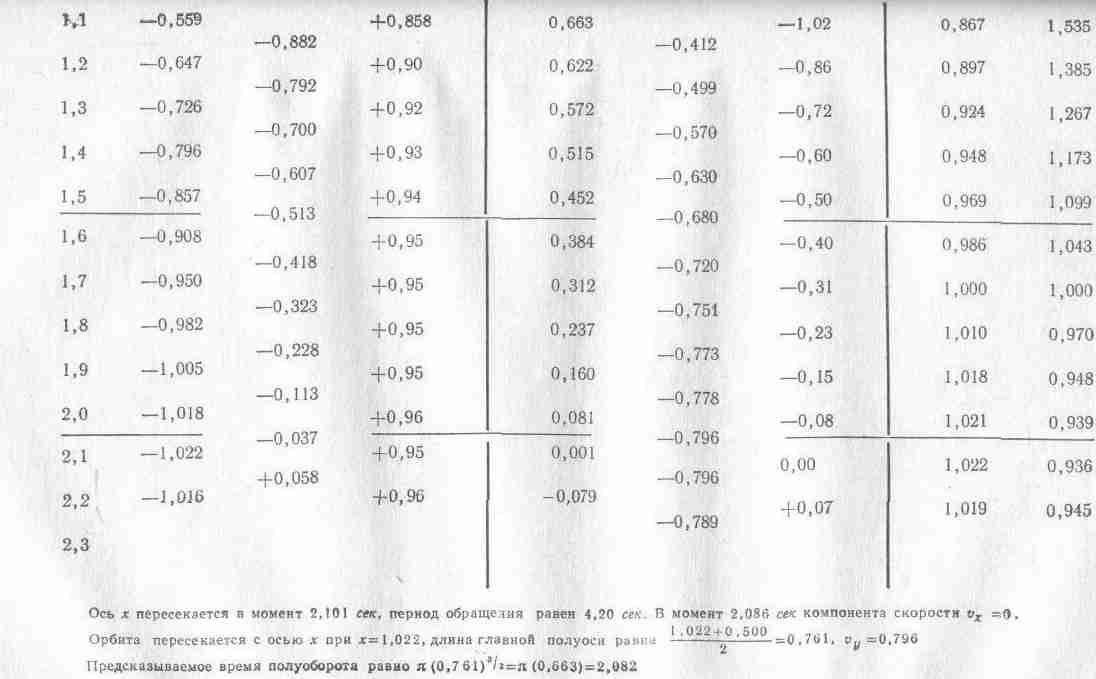 |
 |
и т. д.
В результате мы получим числа, приведенные в табл. 9.2, где приблизительно за 20 шагов прослежена половина пути нашей планеты вокруг Солнца. На фиг. 9.6 отложены координаты планеты х и y, приведенные в табл. 9.2.
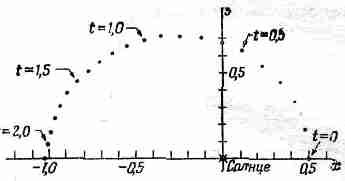 |
Точки представляют собой последовательные положения планеты через каждую десятую долю выбранной нами единицы времени. Видно, что сначала она двигалась быстро, а затем – все медленней и медленней. Видна также и форма кривой движения планеты. Итак, вы теперь знаете, как реально можно вычислять движение планет!
Давайте посмотрим теперь, как вычислить движение Нептуна, Юпитера, Урана и остальных планет. Можно ли сделать подробные расчеты со множеством планет, учитывая к тому же и движение Солнца? Разумеется, можно. Найдем сначала силу, действующую на каждую данную планету, например на ту, которую мы обозначим номером i и координаты которой хi, yi и zi (i=1 может означать Солнце, i=2 – Меркурий, i=3 – Венеру и т. д.). Наша задача – найти координаты всех планет. По закону тяготения x–компонента силы, действующая на i–ю планету со стороны планеты номер j' с координатами хj уj, zj, будет равна –Gmimj(xi–xj)/r3jj . Если же учесть силы со стороны всех планет, то получим следующую систему уравнений:
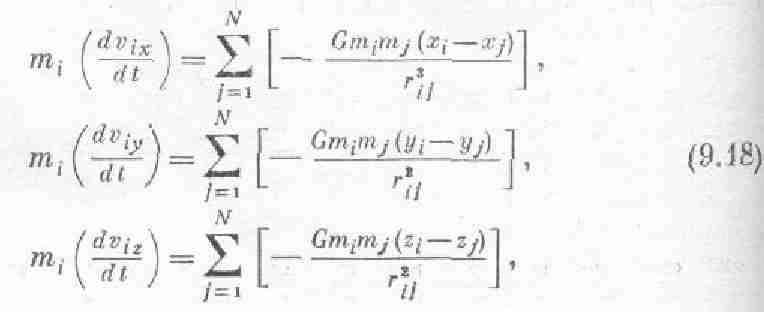 |
где rij – расстояние между i–й и j–й планетами:
 |
? означает суммирование по всем остальным планетам, r. е. по всем значениям j, за исключением, конечно, j = i. Таким образом, чтобы решить это уравнение, нужно лишь значительно увеличить количество столбцов в нашей таблице. Для движения Юпитера понадобится девять столбцов, для Сатурна – тоже девять и т. д. Если нам заданы все начальные положения и скорости, то из уравнения (9.18) можно подсчитать все ускорения, вычислив, конечно, предварительно по формуле (9.19) все расстояния rij,. А сколько же времени потребуется на все эти вычисления? Если вы будете делать их сами дома, то очень много! Однако сейчас уже имеются машины, неимоверно быстро выполняющие все арифметические расчеты. Сложение, например, такая машина выполняет за 1 мксек, т. е. за одну миллионную долю секунды, а умножение – за 10 мксек. Так что если один цикл расчетов состоит из 30 операций умножения, то это займет всего лишь 300 мксек, или за 1 сек можно сделать 3000 циклов. Если мы хотим считать с точностью до одной миллиардной, то для того, чтобы покрыть все время обращения планеты вокруг Солнца, требуется 4•105 циклов. (Оказывается, что ошибка в расчетах приблизительно пропорциональна квадрату ?. Если брать интервал в тысячу раз меньший, то ошибка уменьшится в миллион раз. Так что для обеспечения нашей точности нужно взять интервал в 10 000 раз меньше.) На машине это займет 130 сек, или около 2 мин. Всего лишь 2 мин, для того чтобы «прогнать» Юпитер вокруг Солнца и при этом еще с точностью до одной миллиардной учесть все возмущения от других планет!
Итак, в начале этой главы для вас были загадкой движения грузика на пружинке, однако теперь вооруженные таким мощным орудием, как законы Ньютона, вы можете вычислять не только такие простые явления, как качание грузика, но и неимоверно сложные движения планет, причем с любой желаемой точностью! Нужна только машина, знающая арифметику.
Глава 10 ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА
§ 1. Третий закон Ньютона
Второй закон Ньютона, который связывает ускорение любого тела с действующей на него силой, позволяет хотя бы в принципе решить любую механическую задачу. Можно, например, с помощью числового метода, знакомого вам уже по предыдущей главе, определить движение нескольких частиц. Однако имеется еще достаточно причин, чтобы продолжить изучение законов Ньютона. Во–первых, существуют такие сравнительно простые случаи движения, которые можно изучать не только числовым путем, но и с помощью прямых математических методов. Вы знаете, например, что ускорение свободно падающего тела постоянно и равно 9,8
Одна из таких задач – движение планеты вокруг Солнца. Можно, конечно, так же, как мы это делали в гл. 9, постепенно найти общую форму орбиты, однако и эта задача решается точно, причем в результате получается строго эллиптическая орбита.
Но, к сожалению, таких задач, которые могут быть точно решены с помощью анализа, очень мало. В том же гармоническом осцилляторе, например, если сила пружины не будет пропорциональна отклонению от положения равновесия, а окажется несколько сложнее, мы уже не сможем ничего поделать и вынуждены обращаться к численному расчету. Или, например, если вокруг Солнца вращается не одна планета, а две (т. е. имеются всего три тела, взаимодействующих друг с другом), то нам не удастся найти аналитическую форму такого движения и на деле задача тоже решается численно. Это знаменитая проблема трех тел, над которой в течение долгого времени бились лучшие умы человечества. Интересно, что, пока люди поняли ограниченные возможности математического анализа и необходимость использования числовых методов, потребовалось немало времени. Сейчас с помощью этих методов решается огромное количество задач, которые не могли быть решены аналитически. Та же знаменитая проблема трех тел, решение которой, как полагали, очень сложно, в числовом методе выглядит самой заурядной задачкой и решается способом, описанным в предыдущей главе, т. е. с помощью большого числа арифметических действий. Однако имеются ситуации, когда оба метода оказываются бессильны: простые задачи решаются аналитически, а задачи посложнее – числовым арифметическим методом, но очень сложные задачи невозможно решить ни так, ни этак. Возьмите, например, сложную задачу столкновения двух автомобилей или даже движение молекул газа. В кубическом миллиметре газа содержится бесчисленное количество частиц, и было бы безумием пытаться решать задачу со столькими переменными (около 1017, т. е. сто миллионов миллиардов!). Столь же сложна задача о движении звезд в шаровом скоплении, где вместо двух или трех планет, движущихся вокруг Солнца, собрано громадное количество звезд. Эти проблемы нельзя решить прямыми методами, и нужно изыскать какие–то другие пути.
При таком положении, когда детальное рассмотрение невозможно, полезно знать некоторые общие свойства, т. е. общие теоремы или принципы, которые являются следствием законов Ньютона. Один из таких принципов – это закон сохранения энергии, который мы обсуждали в гл. 4. Вторым принципом является закон сохранения импульса, которому посвящена настоящая глава. Другая причина необходимости дальнейшего изучения механики – это существование некоторых общих свойств движения, которые повторяются при различных обстоятельствах; так что полезно изучить это свойство на каком–то одном частном случае. Мы, например, будем изучать столкновения; различные виды столкновений имеют много общего. Или возьмем течение жидкости, неважно какой; законы течения разных жидкостей имеют много общего. Еще один пример, который мы будем изучать, это колебания, или осцилляции, в частности свойства механических волн: звука, колебания стержней и т. д.
Когда мы обсуждали законы Ньютона, то уже говорили о том, что они являются своего рода программой, которая призывает нас обратить особое внимание на силы. Но о самих силах Ньютон сказал только две вещи. Он полностью сформулировал закон для сил тяготения, но почти ничего не знал о более сложных силах, например о силах между атомами. Однако он открыл одно правило, одно общее свойство всех сил, которое составляет Третий закон. Таким образом, все, что Ньютон знал о природе сил, – это закон тяготения и общий принцип, который гласит:
Означает это примерно следующее. Пусть имеются два маленьких тела, скажем две частицы, и пусть первая из них толкает вторую с некоторой силой. Тогда в соответствии с Третьим законом Ньютона вторая частица будет толкать первую с той же силой, но в противоположную сторону. Более того, эти силы будут действовать вдоль одной и той же линии. Эта гипотеза, или, если хотите, закон, предложенный Ньютоном, выполняется с большой точностью, хотя, впрочем, он не абсолютно точен (с нарушениями его мы познакомимся позднее). Сейчас, однако, мы будем считать его совершенно точным. Разумеется, если есть еще третья частица, которая расположена не на той же линии, что две первые, то закон вовсе
§ 2. Закон сохранения импульса
Давайте посмотрим, чем интересен Третий закон Ньютона. Предположим для простоты, что имеются только две взаимодействующие частицы – частица 1 и частица 2, масса которых может быть различна. К какому следствию приводит равенство и противоположная направленность сил между ними? Согласно Второму закону, сила равна скорости изменения импульса со временем, так что скорость изменения импульса частицы 1 равна скорости изменения импульса частицы 2, т. е.
dp1/dt=dp2/dt (10.1)
Но если
(dp1+dp2)/dt=0. . (10.2)
Напомним еще раз, что в нашей задаче мы предполагаем отсутствие каких–либо других сил, кроме внутренних. Но равенство нулю скорости изменения этой суммы означает просто, что величина (p1+p2) не изменяется с течением времени. (Эта величина записывается также в виде
Рассмотрим теперь картину посложнее, когда есть три или большее число взаимодействующих частиц. Очевидно, что если существуют только внутренние силы, то полный импульс всех частиц остается постоянным, поскольку увеличение импульса одной частицы под воздействием другой частицы в точности компенсируется уменьшением импульса этой второй частицы из–за противодействия первой, т. е. внутренние силы так сбалансированы, что полный импульс всех частиц измениться не может. Таким образом, если нет сил, действующих на систему извне (внешних сил), то ничто не может изменить ее полный импульс и, следовательно, он остается постоянным.
Но нужно еще сказать о том, что произойдет, если будут еще существовать какие–то другие силы, кроме сил взаимодействия между частицами. Предположим, что мы изолировали систему взаимодействующих частиц. Если имеются только взаимные силы, полный импульс, как и прежде, меняться не будет, сколь бы сложны ни были эти силы. Если, однако, существуют силы, обусловленные частицами вне этой изолированной группы, то, как мы докажем позднее, сумма всех этих
Закон сохранения полного импульса некоторого числа взаимодействующих частиц в отсутствие внешних сил можно записать в виде
m1v1+m2v2 +m3v3+
где mi и vi – просто масса и скорость частицы соответствующего номера. Однако для каждой из этих частиц Второй закон Ньютона
f=(d/dt)(mv) (10.4)
пишется для любой
Точно такие же формулы можно написать для
Существует еще одно интересное следствие Второго закона Ньютона, кроме закона сохранения импульса. Доказательством его мы будем заниматься позднее, а сейчас я просто расскажу вам о нем. Следствие или, скорее, принцип состоит в том, что законы физики не изменяются от того, стоим ли мы на месте или движемся равномерно и прямолинейно. Пусть, например, на быстро летящем самолете ребенок играет с мячиком. Наблюдательный ребенок сразу заметит, что мячик прыгает точно так же, как и на земле. Иначе говоря, законы движения для ребенка в самолете (если только последний не меняет скорости) выглядят одинаково как на поле аэродрома, так и в полете. Этот факт известен под названием
Таким образом, из закона Ньютона мы вывели закон сохранения импульса, а теперь давайте посмотрим, какие специфические законы описывают соударение и рассеяние частиц. Однако для разнообразия, а также чтобы продемонстрировать типичные рассуждения, которыми мы часто пользуемся в физике в других случаях, когда, скажем, не известны законы Ньютона и должен быть принят иной метод рассмотрения, давайте обсудим законы рассеяния и соударения с совершенно другой точки зрения. Мы будем исходить из принципа относительности Галилея и в конце рассуждений придем к закону сохранения импульса.
Итак, начнем с утверждения, что законы природы не изменяются от того, что мы движемся прямолинейно с некоторой скоростью или стоим на месте. Однако прежде чем обсуждать процессы, в которых два тела сталкиваются и слипаются или разлетаются в стороны, давайте рассмотрим случай, когда эти два тела связаны между собой пружинкой или чем–то в этом роде, а затем вдруг освобождаются и разлетаются под действием этой пружинки или, быть может, небольшого взрыва в разные стороны. Кроме того, рассмотрим движение только в одном направлении. Предположим сперва, что эти два тела совершенно одинаковы и расположены симметрично. Когда между ними произойдет взрыв, одно из них полетит направо с некоторой скоростью
Таким образом, первый результат нашего эксперимента – одинаковые тела имеют одинаковую скорость. Но предположим теперь, что тела сделаны из различного материала, скажем один из меди, а другой из алюминия, но
Пусть из предыдущего эксперимента нам известно, что два куска вещества
Возьмем еще один пример. Пусть при некоторой силе взрыва установлено, что масса
Итак, в дальнейших рассуждениях мы будем считать, что равные массы разлетаются в противоположные стороны с равными скоростями, если между ними происходит взрыв. А что произойдет, если мы обратим задачу, т. е. если два одинаковых тела, летящие навстречу друг другу с равными скоростями, сталкиваются и слипаются вместе? Как будут они двигаться? Здесь опять на помощь приходят соображения симметрии (т. е. что между левой и правой сторонами нет никакого различия), из которых следует, что образовавшееся тело должно стоять на месте. Мы будем также предполагать, что два тела с равной массой, летящих навстречу друг другу, даже если они сделаны из различного материала, после столкновения и слипания остановятся.
§ 3. Импульс всё–таки сохраняется!
Можно экспериментально проверить наши предположения о том, что, во–первых, покоящиеся два тела с равной массой, разорванные взрывом, полетят в разные стороны с равной скоростью и, во–вторых, что два тела, обладающие равными скоростями и массами, при соударении и слипании останавливаются. Такую проверку можно сделать с помощью замечательного устройства – воздушного желоба (фиг. 10.1).
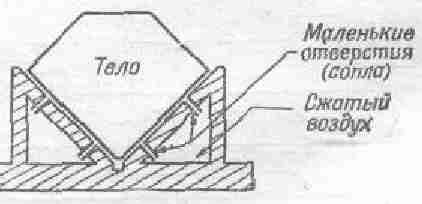 |
В этом устройстве нет никаких трущихся деталей – вопрос, который очень беспокоил Галилея. Он не мог поставить эксперимента со скользящими телами, ибо они не скользили свободно, но о помощью чудесного желоба мы можем теперь избавиться от трения. Наши тела будут лететь без помех, а скорость их, согласно предвидению Галилея, будет оставаться постоянной. Это достигается тем, что тело поддерживается воздушной подушкой, а поскольку трение о воздух очень мало, то тело планирует практически с постоянной скоростью, если на него не действуют никакие силы. Возьмем сначала два скользящих бруска, вес или массы которых с большой точностью равны друг другу (практически измеряется вес, но он, как вы знаете, пропорционален массе), и поместим между ними небольшой взрыватель в закрытом цилиндре (фиг. 10.2).
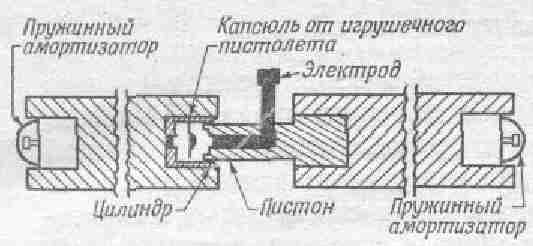 |
Фиг. 10.2. Продольный разрез скользящего бруска, скрепленного со взрывным цилиндром.
Всю эту систему устанавливаем в центре желоба и электрической искрой поджигаем взрыватель. Что же произойдет? Если массы брусков одинаковы, то они, разлетевшись в стороны, одновременно достигнут концов желоба. Там они отскакивают от ограничителей, сталкиваются и слипаются в центре, точно в том же месте, откуда разлетелись (фиг. 10.3).
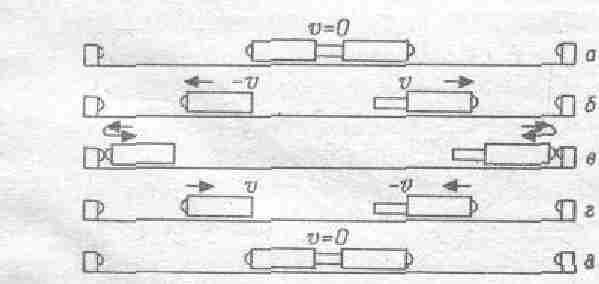 |
Это интересный опыт. И в действительности происходит все так, как мы рассказали.
Теперь на очереди проблема посложнее. Допустим, мы имеем две массы, причем одна движется со скоростью
 |
Фиг. 10.4, Неупругое соударение равных масс.
Наконец, образовавшееся после соударения и слипания тело будет казаться нам летящим со скоростью
Точно таким же образом можно определить, что произойдет, когда сталкиваются два одинаковых тела, каждое из которых движется с
Пусть одно тело летит со скоростью
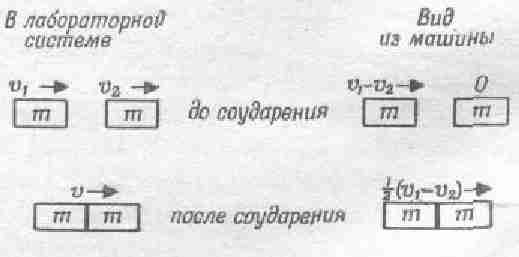 |
Фиг. 10.5. Другой случай неупругого соударения равных масс.
Обратите внимание, что снова
mv1+ mv2=m•1/2 (v1+v2). (10.6)
Таким образом, принцип относительности Галилея помогает нам разобраться в любом соударении равных масс. До сих пор мы рассматривали движение в одном измерении, однако на основе его становится ясным многое из того, что будет происходить в более сложных случаях соударения: нужно только пустить автомобиль не вдоль направления движения тел, а под каким–то углом. Принцип остается тем же самым, хотя детали несколько усложняются.
Чтобы экспериментально проверить, действительно ли тело, летящее со скоростью
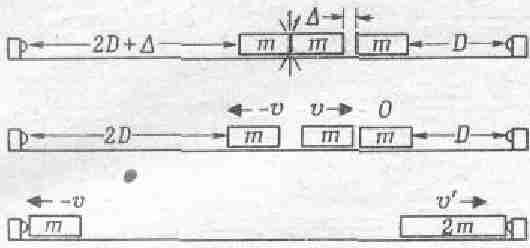 |
Следующая проблема, которую мы должны решить: что получится, если тела имеют разные массы. Давайте возьмем массы m и 2m и устроим между ними взрыв. Что произойдет тогда? С какой скоростью полетит масса
Перейдем теперь к следующему вопросу. Что произойдет, если тело с массой m и скоростью
 |
Скорости, которые мы при этом увидим, будут равны
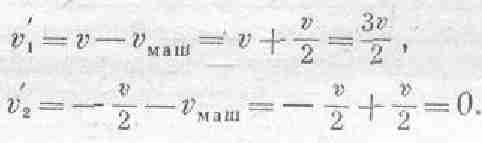 |
После соударения масса 3m покажется нам движущейся со скоростью
Итак, мы рассмотрели столкновение одного тела с двумя. Используя те же рассуждения, можно предсказать результаты столкновения одного тела с тремя телами, двух тел с тремя телами и т. д. На фиг. 10.8 как раз показан случай разлета масс
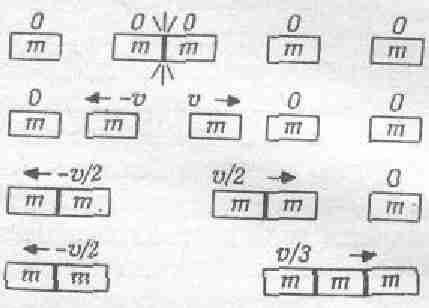 |
В каждом из этих случаев выполняется одно и то же правило: масса первого тела, умноженная на его скорость, плюс масса второго тела, умноженная на его скорость, равны произведению полной массы на скорость ее движения. Все это – примеры сохранения импульса. Итак, начав с простого случая симметричных равных масс, мы установили закон сохранения для более сложных случаев. В сущности это можно сделать для любого рационального отношения масс, а поскольку любое число может быть со сколь угодно большой точностью заменено рациональным, то закон сохранения импульса справедлив для любых масс.
§ 4. Импульс и энергия
Во всех предыдущих примерах мы рассматривали только случаи, когда два тела сталкиваются и слипаются или с самого начала были скреплены вместе, а потом разделяются взрывом. Однако существует множество примеров соударений, в которых тела
Тот факт, что скорости
Точно таким же способом можно разобрать случай соударения тел с различными массами, различными начальными скоростями, различными упругостями и определить конечные скорости и потерю кинетической энергии; но мы не будем сейчас подробно разбирать эти явления.
Упругое соударение особенно часто встречается между системами, у которых нет никаких внутренних механизмов, никаких «шестеренок, маховиков или других частей». В таких случаях кинетическая энергия не может ни на что растратиться: ведь разлетающиеся тела находятся в тех же условиях, что и налетающие. Поэтому между элементарными объектами соударение всегда или почти всегда упругое. Говорят, например, что соударение между атомами и молекулами абсолютно упругое. Хотя это действительно очень хорошее приближение, но и эти соударения не
Давайте разберем интересный пример
Другой пример почти абсолютно упругого взаимодействия дает нам магнетизм. Положите пару U–образных магнитов на наши скользящие бруски в воздушном желобе так, чтобы они отталкивались друг от друга. Если теперь потихоньку подтолкнуть один из брусков к другому, то он, не касаясь, оттолкнет его, а сам остановится. Второй же брусок полетит вперед.
Закон сохранения импульса – очень полезная штука. Он позволяет решить многие проблемы, не входя в детали процесса. Нас, например, совершенно не интересовали детали движения газа при взрыве заряда, но тем не менее мы могли предсказать, во сколько раз одно тело будет двигаться быстрее второго при их разлете. Другой интересный пример – это ракетный двигатель. Ракета большой массы
§ 5. Релятивистский импульс
Уже на нашей памяти закон сохранения импульса претерпел некоторые изменения. Они, однако, не коснулись самого закона как такового, просто изменилось понятие импульса. В теории относительности, как оказалось, импульс уже не сохраняется, если его понимать так же, как и прежде. Дело в том, что масса не остается постоянной, а
 |
где m0– масса покоящегося тела,
 |
Компоненты импульса для одной частицы можно записать в виде
где
В гл. 4 мы уже видели, что закон сохранения энергии неверен, если мы не признаем эквивалентности энергии во всех ее формах, т. е. электрической энергии, механической энергии, энергии излучения, тепловой и т. д. Про некоторые из этих форм, например тепло, можно сказать, что энергия «скрыта» в них. Напрашивается вопрос: а не существуют ли также «скрытые» формы импульса, скажем «тепловой импульс»? Дело в том, что импульс утаить невозможно; скрыть его очень трудно по следующим причинам.
Мера тепловой энергии – случайного движения атомов тела – представляет собой просуммированные
Ньютон считал, что взаимодействие на расстоянии должно быть мгновенным. Но это, оказывается, неверно. Возьмем, например, электрические силы. Пусть электрический заряд, расположенный в некоторой точке, вдруг начинает двигаться, тогда его действие на другой заряд в другой точке не будет мгновенным: существует небольшое запаздывание. При таком положении, даже если силы действия и противодействия равны между собой, импульсы не будут компенсироваться. Существует небольшой промежуток времени, в течение которого будет происходить нечто странное; в то время как первый заряд испытывает какое–то воздействие силы и реагирует на нее изменением своего импульса, второй стоит как ни в чем не бывало и не изменяет импульса. На передачу влияния второму заряду через разделяющее их расстояние требуется некоторое время: «влияние» распространяется не мгновенно, а с некоторой конечной (хотя и очень большой) скоростью 300 000
Оказывается, что в квантовой механике импульс тоже не mv, а нечто совсем другое. Здесь уже трудно определить точно, что же такое скорость частицы, но импульс все–таки существует. Разница же состоит в том, что когда частицы действуют как частицы, то их импульс по–прежнему
Глава 11 ВЕКТОРЫ
§ 1. Симметрия в физике
В этой главе мы вводим понятие, которое среди физиков известно под названием
Предположим, что где–то мы установили сложную машину со множеством зацеплений, с какими–то маховиками, шатунами и т. п. Предположим теперь, что в каком–то другом месте мы собрали такое же устройство, все части которого являются точной копией частей прежней машины, причем сохранены все размеры и ориентация отдельных ее частей, все то же самое, только перенесено на некоторое расстояние. Затем мы запустим обе машины в одинаковых условиях и посмотрим, будут ли они работать совершенно одинаково? Будут ли движения отдельных частей одной машины повторять в точности соответствующие движения другой? Вообще говоря, ответ может быть
Любая физическая идея требует здравого смысла при своем осуществлении, ведь это не чисто математические или абстрактные идеи. Нужно понимать, что мы имеем в виду, когда говорим, что при перенесении какого–либо устройства в другое место наблюдаются те же явления. Под этим мы понимаем, что мы передвигаем все, что можно передвинуть. Если же при этом явление в чем–то изменяется, то мы предположим, что что–то послужило помехой, и займемся изучением причин. Если мы ничего не обнаружим, то объявим, что физические законы не обладают ожидаемой симметрией. Но если физические законы все–таки обладают симметрией, то мы найдем причину помех, во всяком случае мы надеемся найти ее. Осмотревшись, мы обнаружим, например, что работе машины мешает стена. Основной вопрос состоит в следующем: если мы достаточно хорошо изучим наши устройства, если все основные источники сил имеются внутри аппарата и если на другое место передвинуть все, что следовало передвинуть, то будут ли законы меняться? Будет ли машина на новом месте работать так, как раньше?
Ясно, что мы хотим передвинуть само устройство и источники
§ 2. Переносы начала
Мы ограничим наше рассмотрение законами механики, которую достаточно хорошо изучили. В предыдущих главах мы установили, что законы механики можно свести к трем справедливым для любой частицы уравнениям:
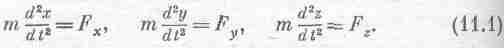 |
Это означает, что существует такой способ
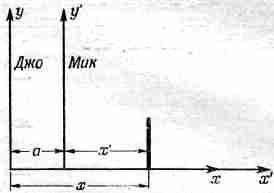 |
Когда Джо определяет положение произвольной точки в пространстве, он находит три ее координаты:
Чтобы сделать наш анализ полным, нужно знать, какие силы измеряет Мик. Если сила действует вдоль произвольной линии, то под силой вдоль направления
Уравнения (11.2) и (11.3) определяют соотношения между величинами, используемыми Джо и Миком.
Теперь поставим вопрос так: если Джо знает законы Ньютона, то будут ли они верны, когда их попробует использовать Мик? Имеет ли значение выбор начала координат? Другими словами, предположим, что уравнения (11.1) верны, а (11.2) и (11.3) определяют соотношения между измеряемыми величинами; верно ли, что
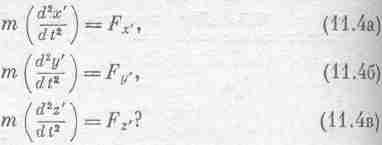 |
Чтобы проверить эти уравнения, дважды продифференцируем выражение для
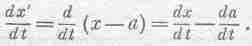 |
Предположим теперь, что начало системы координат, которой пользуется Мик, фиксировано (не движется) относительно системы координат Джо, т. е.
 |
Таким образом, произведения массы на ускорение одинаковы у обоих друзей. Можно получить и формулу для
.
Следовательно, законы механики, с точки зрения Мика, точно такие же: он пишет законы Ньютона в других координатах, и эти законы оказываются верными. Это означает, что центра Вселенной нет и законы движения выглядят одинаково, с какого бы места они ни наблюдались.
Верно и такое утверждение: если в каком–либо месте установить устройство с каким–то механизмом, то и в любом другом месте это устройство будет работать одинаково. Почему? Потому что любая машина, которую изучает Мик, подчиняется тем же уравнениям, которые описывают работу машины, контролируемой Джо. Поскольку
§ 3. Вращения
Разобрав вопрос о перенесении начала координат, мы рассмотрели первую задачу из серии более сложных теорем о симметрии физических законов. Следующая теорема утверждает, что и
Обсудим теперь влияние ориентации системы координат на физические законы. Давайте посмотрим, не будут ли нам снова полезны Мик и Джо. Чтобы избежать ненужных сложностей, предположим, что эти молодые люди находятся в одной точке пространства (мы уже показали, что их системы координат можно перемещать). Пусть оси системы координат Мика повернуты относительно системы координат Джо на угол ?, Обе системы координат изображены на фиг. 11.2, где мы ограничились двумя измерениями.
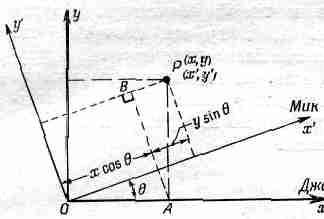 |
Произвольная точка
Теперь (мы поступали так и раньше) установим соотношения между силами, измеряемыми двумя наблюдателями. Предположим, что сила
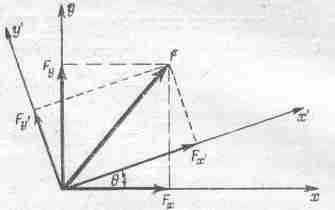 |
Составляющая
Интересно отметить случайность, которая в дальнейшем окажется очень важной: формулы (11.5) и (11.6) для координат
 |
Чтобы проверить эти уравнения, вычислим левые и правые части независимо, а затем сравним результаты. Чтобы вычислить левые части, умножим уравнения (11.5) на m и продифференцируем их дважды по времени, считая угол 9 постоянным. Это дает
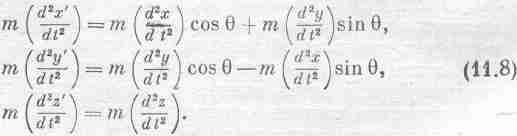 |
Вычислим правые части уравнений (11.7), подставив (11.1] в уравнения (11.6). Получаем
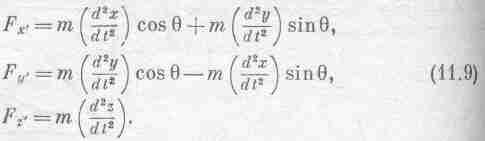 |
Глядите! Правые части уравнений (11.8) и (11.9) тождественны; значит, если законы Ньютона верны в одной системе координат, то ими можно пользоваться и в другой системе. Эти рассуждения заставляют нас сделать некоторые важные выводы: во–первых, никто не может утверждать, что избранная им система координат единственна, она может быть, конечно, более
§ 4. Векторы
Насколько нам известно сейчас, не только законы Ньютона, но и все физические законы обладают двумя свойствами, которые называют инвариантностью (или симметрией) относительно перемещений и поворотов координатных осей. Эти свойства столь важны, что для учета их при изучении физических законов была разработана специальная математическая техника.
Решение поставленных в предыдущих параграфах задач потребовало довольно длинных расчетов. Чтобы свести их к минимуму, изобретен могучий математический аппарат. Эта система, называемая
Заметим, что в физике важно знать величины двух типов (на самом деле их больше двух, но давайте начнем с двух). Величины первого типа, например число картофелин в мешке, мы будем называть обыкновенными числами, или
Все величины, имеющие направление, подобно шагу в пространстве, называются
Вектор определяется тремя числами. Чтобы описать шаг, скажем из начала координат в точку
Предположим теперь, что существует другая направленная величина, например сила – еще одна величина, которую можно определить, задав связанные с ней три числа. Эти три числа переходят при изменении системы координат в другие три числа по строго определенным математическим правилам. Эти правила должны быть теми же самыми, которые определяли переход тройки чисел
F = r
справедливо в
Тот факт, что физические соотношения между какими–либо величинами можно выразить в виде векторных уравнений, говорит о том, что эти соотношения верны в любой системе координат. Вот почему понятие вектора очень удобно в физике.
Давайте теперь рассмотрим некоторые свойства векторов. В качестве примера «вектора» можно указать скорость, импульс, силу и ускорение. Часто бывает удобно изобразить вектор в виде стрелки, указывающей направление действия. Но почему же можно представить силу стрелкой? Да потому, что она преобразуется по тем же законам, что и «шаг в пространстве». Именно поэтому можно представить силу в виде чертежа, как если бы это изображалось перемещение, причем выберем такой масштаб, чтобы единица силы, например ньютон, соответствовала некоторой длине. Проделав такую процедуру однажды, мы всегда сможем изображать силы в виде отрезков, потому что уравнение типа
F=kr
(где
§ 5. Векторная алгебра
Теперь мы должны описать законы, или правила, 'регулирующие возможные сочетания различных векторов. Прежде всего мы изучим
с=а +b.
Вектор с обладает интересным свойством:
с=b+а;
это легко проверить, написав составляющие вектора с. Кроме того,
а+(b+с)=(а+b) + с.
Векторы можно складывать в любом порядке.
Каков геометрический смысл а+b? Как будет выглядеть вектор с, если мы, скажем, изобразим а и b с помощью стрелок? Ответ на этот вопрос дает фиг. 11.4.
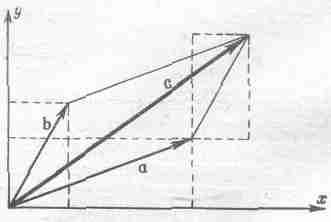 |
Мы видим, что прибавить составляющие вектора b к составляющим вектора а проще всего, приложив соответствующим образом прямоугольник, определяемый составляющими b, к такому же прямоугольнику, определяемому составляющими а. Поскольку а и b хорошо подогнаны к своим прямоугольникам, то это все равно, что поставить вектор b «ногами» на «голову» вектору а. Стрелка, соединяющая «ноги» вектора а и «голову» вектора b, и будет вектором с. Можно поступить иначе: поставить «ноги» а на «голову» b. Вспомнив геометрические свойства параллелограмма, можно убедиться в том, что мы снова получим тот же вектор с. Заметим, что, ставя векторы друг на друга, мы складываем их без помощи координатных осей.
Предположим, что мы умножили вектор а на число а. Что нужно понимать под таким произведением? Договоримся понимать под этим вектор с компонентами
Рассмотрим теперь вычитание векторов. Можно определить вычитание тем же способом, что и сложение, но вместо того, чтобы складывать, будем вычитать составляющие. Можно также определить вычитание как сложение с отрицательным вектором–b=(-1)b. Результат будет тот же.
Вычитание векторов показано на фиг. 11.5.
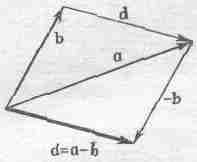 |
На этом чертеже изображено
d=а–b=а+(-b); заметим также, что, зная векторы а и b, разность а–b можно легко найти из эквивалентного соотношения а=b+d. Таким образом найти разность векторов даже легче, чем сумму: просто нужно провести вектор, соединяющий b и а, и вы получите а–b!
Перейдем теперь к скорости. Почему скорость есть вектор? Если координаты точки равны
Постараемся нагляднее представить себе, что такое скорость и почему она вектор. Далеко ли продвинется частица за малое время ?t?
Иначе говоря, под вектором скорости мы понимаем предел разности радиус–векторов, соответствующих моментам t+?t и
 |
Скорость есть вектор постольку, поскольку она равна разности двух векторов. Это верно также и потому, что составляющие этого вектора равны
§ 6. Законы Ньютона в векторной записи
Чтобы записать законы Ньютона в векторной форме, мы должны поучиться еще кое–чему и определить вектор ускорения. Этот вектор равен производной по времени вектора скорости, причем легко показать, что его составляющие равны вторым производным
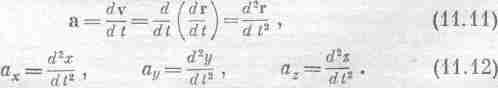 |
После этого законы Ньютона можно записать таким образом: или ma = F, (11.13)
m(d2r/dt2)=F (11.14)
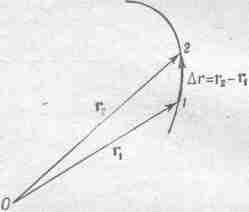 |
Теперь задача о доказательстве инвариантности законов Ньютона относительно вращений сводится к следующему: нужно доказать, что а (ускорение) есть вектор; это мы уже сделали. Затем нужно доказать, что F (сила) есть вектор; это мы
Тот факт, что ускорение – это скорость изменения вектора скорости, помогает найти ускорение в любых, казалось бы, трудных обстоятельствах. Предположим, например, что частица, двигаясь по какой–то сложной кривой (фиг. 11.7), имеет в момент t1 скорость v1, а несколько позже, в момент t2
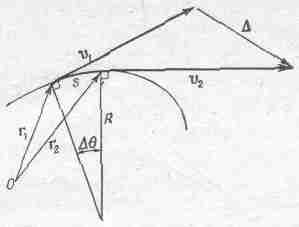 |
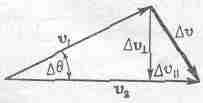 |
Теперь можно поговорить об ускорении. Ускорение, конечно, просто равно ?v/?t. Интересно заметить, что разность скоростей можно разделить на две части: можно представить себе, что ускорение состоит из
a?=dv/dt. (11.15)
Другую, поперечную составляющую ускорения легко вычислить, взглянув на фиг. 11.7 и 11.8. За короткое время ?t изменение угла между v1 и v2 равно малому углу ??. Если величина скорости равна
?v?=v??, а ускорение а равно
а?=v(d?/dt).
Теперь нам нужно знать ??/?t. Эту величину можно найти так: если в данный момент кривую можно приблизительно заменить окружностью радиусом R, то, поскольку за время ?t частица пройдет расстояние s=v?t, изменение угла равно
??=v(?t/R) или ??/?t=v/R.
Таким образом, как мы уже установили ранее,
a=v2/R. (11.16)
§ 7. Скалярное произведение векторов
Давайте еще немного займемся свойствами векторов. Легко понять, что
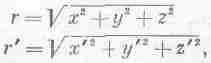 |
а затем проверить, что эти обе величины равны. Чтобы не возиться с квадратным корнем, будем сравнивать квадраты расстояний. Мы должны, таким образом, показать, что
Подставив в это уравнение определяемые соотношением (11.5) значения ж',
Незаметно мы получили новый тип величин. Мы можем построить функцию
a•a=a2x+ a2y+a2z. (11.18)
Вы спросите: «В какой системе координат?» Но раз это число не зависит от системы координат, то ответ одинаков в
a•b
то можно убедиться, что эта величина совпадает в штрихованной и нештрихованной системах координат. Чтобы доказать это, заметим, что это верно для величин а•а, b•b и с•с, где с=а+b. Сумма квадратов
Раскроем скобки в обеих сторонах этого уравнения. Перекрестные произведения дадут нам выражения типа (11.19), а суммы квадратов составляющих а и b – выражения (11.18). Инвариантность слагаемых типа (11.18) приводит к инвариантности перекрестных произведений типа (11.19).
Величина а•b называется
а• (b+c)=а•b+а•с. (11.21)
Есть еще очень простой геометрический способ вычисления а•b, при котором не надо определять составляющих а и b; просто а•b есть произведение длин векторов а и b на косинус угла между ними. Почему? Предположим, что мы выбрали такую систему координат, в которой вектор а направлен вдоль оси
а•b=
Таким образом, в этой частной системе координат мы доказали, что a•b равно произведению длин векторов а и b на косинус угла между ними 9. Но
Что хорошего может дать нам эта новая величина? Нужно ли физику скалярное произведение? Да, оно необходимо ему постоянно. Например, в гл. 4 мы назвали кинетической энергией величину
Энергия не имеет направления. Импульс же направление имеет, это – вектор, и он равен произведению массы на вектор скорости.
Другим примером скалярного произведения может служить работа, произведенная силой при перемещении какого–нибудь предмета с одного места на другое. Мы еще не дали определения работы, она равна изменению энергии, прибавке в весе, после того как сила F поработает вдоль пути s:
Работа=F•s. (11.23)
Иногда целесообразно говорить о составляющей вдоль определенного направления (например, вдоль вертикали, потому что это направление силы тяжести). Для этого удобно ввести
Предположим, что нам задана какая–то система координат
j – единичный вектор вдоль оси y и к – единичный вектор вдоль оси z. Ясно, что i•i=l. Чему же равно произведение i•j? Если угол между векторами прямой, то их скалярное произведение равно нулю. Таким образом,
i•i=1,
i•j = 0, j•j=1, (11.24) i•k=0, j•k=0, k•k=l.
Используя эти свойства векторов i, j, k, можно записать любой вектор а в виде
Таким образом, можно от составляющих вектора легко перейти к самому вектору.
Мы изучили далеко не все свойства векторов. Однако, прежде чем углубиться в этот вопрос, научимся сперва применять обсужденные сейчас идеи в физике. И тогда, когда мы хорошо овладеем основным материалом, будет легче продвинуться дальше, не впадая в ошибки. Позднее мы увидим, что удобно определить еще одно произведение двух векторов, которое называется векторным произведением и записывается в виде аXb. Однако обсуждение этого вопроса лучше отложить до следующей главы.
 |
§ 1, Что есть сила?
Хотя изучение законов физики интересно и поучительно, хотя они и помогают нам понимать природу и овладевать ее силами, все же порой стоит остановиться и поразмыслить: что же они на самом деле значат? Смысл любого утверждения – вещь, которая издавна, с незапамятных времен, интересовала и тревожила философов, а уж смысл физических законов тем более должен волновать нас, ведь повсеместно считается, что в этих законах таятся некоторые реальные знания. Смысл истины – это глубочайший философский вопрос; всегда важно вовремя спросить: что это значит?
Спросим же: в чем смысл физических законов Ньютона, в чем смысл формулы F=ma? В чем смысл силы, массы и ускорения? Мы интуитивно понимаем, что такое масса; мы можем также
Имеется, положим, закон, что импульс сохраняется тогда, когда сумма внешних сил равна нулю. И вот у нас спрашивают: «А что это
Пусть, например, мы бы решились говорить, что тело, предоставленное самому себе, лежит на месте и не движется; тогда, заметив, что что–то движется, мы бы стали утверждать, будто на него действует «жила» – мера охоты к перемене мест. Мы получили бы прекрасный новый закон, все было бы хорошо, кроме тех случаев, когда действует «жила». Как видите, все было бы подобно нашему определению силы и точно так же не несло бы в себе никакой информации. Истинное же содержание законов Ньютона таково: предполагается, что сила обладает
Первый пример таких сил – полный закон тяготения, предложенный Ньютоном. Формулируя свой закон, он отвечал на вопрос: что такое сила? Если бы ничего, кроме тяготения, не существовало, то сочетание этого закона и закона силы (второго закона движения) оказалось бы завершенной теорией. Но, кроме тяготения, существует и многое другое, и мы собираемся пользоваться законами Ньютона во всевозможных положениях. Поэтому нам придется кое–что порассказать о свойствах сил.
К примеру, говоря о силе, мы всегда неявно предполагаем, что когда нет физических тел, то сила равна нулю. Если мы видим, что сила не равна нулю, мы ищем по соседству ее
Одна из важнейших характеристик силы – ее материальное происхождение; и это свойство как раз
Ньютон привел еще одно правило, касающееся сил: силы между взаимодействующими телами равны и противоположны; действие равно противодействию. И это правило, оказывается, не совсем верно. Да и сам закон F=ma не совсем верен; будь он определением, мы бы должны были утверждать, что он точно верен
Вы можете заявить: «А мне не нравится эта неточность, я хочу, чтобы все определялось точно, да и во многих книжках написано, что наука – вещь точная, что в ней
Любое простое высказывание является приближенным; в виде примера рассмотрим некоторый предмет… кстати,
Стоит услышать это и сразу становится ясно, что они сами не понимают того, о чем говорят.
Эта система ничем не похожа на математические рассуждения. В них все может быть определено, и в итоге всегда
Действительно, ведь все великолепие математики в том и состоит, что
Конечно, с экспериментальной (а не математической) точки зрения вам нужно знать, применимы ли законы Евклида к тому роду геометрии, которую вы используете, измеряя окрестности; вы предполагаете, что да, применимы. И, действительно, они прекрасно работают; прекрасно, но не точно, потому что ваши съемочные линии– это не настоящие геометрические линии. Приложимы или нет абстрактные евклидовы прямые к линиям, провешиваемым на опыте, – есть дело самого опыта; на этот вопрос чистым рассуждением не ответить.
Точно таким же образом вы не можете назвать F=ma определением, вывести из него все чисто математически и сделать механику математической теорией: механика – это описание природы. Выдвигая подходящие постулаты, всегда можно создать математическую систему вроде евклидовой, но вы не можете создать математики мира; рано или поздно вам пришлось бы отвечать на вопрос: выполняются ли эти аксиомы на объектах природы? И вы немедленно завязли бы среди этих запутанных, «нечистых» реальных предметов, – правда, добиваясь все большей и большей точности приближений.
§ 2. Трение
Итак, чтобы по–настоящему понять законы Ньютона, мы должны обсудить свойства сил; цель этой главы – начать это обсуждение и составить своего рода дополнение к законам Ньютона. Мы уже знакомы со свойствами ускорения и с другими сходными представлениями, теперь же нам предстоит заняться свойствами сил. Из–за сложности их мы в этой главе (в отличие от прежних) не будем гнаться за точными формулировками. Чтобы начать с конкретной силы, рассмотрим сопротивление, которое воздух оказывает летящему самолету. Каков закон этой силы? (Мы
Каково же положение этого закона среди других? Подобен ли он закону F=ma? Отнюдь. Во–первых, он эмпирический, и получен он грубыми измерениями в аэродинамической трубе. Но вы возразите: «Что ж, закон F=ma тоже мог бы быть эмпирическим». Но разве в этом дело? Различие не в эмпиричности, а в том, что, насколько мы понимаем, этот закон трения есть результат множества влияний и в основе своей ничуть не прост. Чем больше мы станем его изучать, чем точнее мерить, тем
Во–вторых, есть и другие сложности: можно ли, скажем, эту силу делить на части, – на силу трения крыльев, фюзеляжа, хвоста и т. д.? Конечно, когда нужно бывает узнать вращательные моменты, действующие на части самолета, то так делать можно, но тогда уж надо иметь специальный закон трения для крыльев и т. д. И выясняется тот удивительный факт, что сила, действующая на крыло, зависит от другого крыла, т. е. если убрать самолет и оставить в воздухе одно крыло, то сила будет совсем не такой, какой она была бы, если бы в воздухе был весь самолет, Причина, конечно, в том, что ветер, бьющий в нос самолета, стекает на крылья и меняет силу торможения. И хотя кажется чудом, что существует такой простой, грубый эмпирический закон, пригодный для создания самолетов, но он не из тех законов физики, которые называют
Мы только что говорили о двух типах трения, возникающих в результате быстрого движения в воздухе или медленного в меде. Но есть еще вид трения – сухое, или трение скольжения: о нем говорят тогда, когда одно твердое тело скользит по другому. Чтобы продолжать движение, такому телу нужна сила. Ее называют силой трения. Происхождение ее – вопрос очень запутанный. Обе соприкасающиеся поверхности неравномерны, если разглядывать их на атомном уровне. В точках соприкосновения атомы сцепляются; при нажиме на тело сцепка рвется и возникают колебания (во всяком случае, происходит нечто похожее). Прежде думали, что механизм трения несложен: поверхность покрыта неровностями и трение есть результат подъема скользящих частей на эти неровности; но это неправильно, ведь тогда бы не было потерь энергии, а на самом деле энергия на трение тратится. Механизм потерь иной: неровности при скольжении сминаются, возникают колебания и движение атомов, и тепло растекается по обоим телам. И здесь крайне неожиданным оказывается, что эмпирически это трение можно приближенно описать простым законом. Сила, нужная для того, чтобы преодолевать трение и тащить один предмет по поверхности другого, зависит от силы, направленной по нормали (но перпендикуляру) к поверхностям соприкосновения. В довольно хорошем приближении можно считать, что сила трения пропорциональна нормальной силе с более или менее постоянным коэффициентом:
где ? –
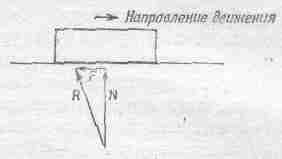 |
Хотя коэффициент ? не очень постоянен, эта формула оказывается хорошим эмпирическим правилом, позволяющим прикидывать, какая сила понадобится в тех или иных практических или инженерных обстоятельствах. Только когда нормальная сила или быстрота движения очень уж велика, закон отказывает: выделяется чересчур много тепла. Важно понимать, что у любого из этих эмпирических законов есть ограничения, вне которых они не работают.
Приближенную справедливость формулы F=?N можно засвидетельствовать простым опытом. Положим брусок весом
Когда проделываешь этот опыт, легко заметить, что при правильном угле наклона 8 брусок скользит не непрерывно, а с остановками: на одном месте он застрянет, а на другом рванется вперед. Такое поведение есть признак того, что коэффициент трения только грубо можно считать постоянным: он меняется от места к месту. Столь же неуверенное поведение наблюдается и при изменении нагрузки бруска. Различия в трении возникают от разной гладкости или твердости частей поверхности, от грязи, ржавчины и прочих посторонних влияний. Таблицы, в которых перечислены коэффициенты трения «стали по стали», «меди по меди» и прочее, – все это сплошное надувательство, ибо в них этими мелочами пренебрегают, а ведь они–то и определяют значение ?. Трение «меди о медь» и т. д. – это на самом деле трение «о загрязнения, приставшие к меди».
В опытах описанного типа трение от скорости почти не зависит. Многие верят, что трение, которое нужно преодолеть, чтобы привести предмет в движение (статическое), больше силы, необходимой для поддержания уже возникшего движения (трение скольжения). Но на сухих металлах трудно заметить какую–либо разницу. Мнение это порождено, вероятно, опытами, в которых присутствовали следы масла или смазки, а может быть, там бруски закреплялись пружинкой или чем–нибудь гибким, как бы привязываясь к опоре.
Очень трудно добиться точности в количественных опытах по трению, и до сей поры трение не очень хорошо проанализировано, несмотря на огромное значение такого анализа для техники. Хотя закон
Раньше было уже сказано, что попытки измерить ? при скольжении чистых веществ (медь по меди) ведут к сомнительным результатам, потому что соприкасающиеся поверхности – не чистая медь, а смеси окислов и прочих загрязнений. Если мы хотим получить совершенно чистую медь, если мы вычистим и отполируем поверхности, дегазируем вещество в вакууме и соблюдем все необходимые предосторожности, то все равно ? мы не получим. Потому что два куска меди слипнутся, и тогда хоть ставь плоскость торчком! Коэффициент ?, для умеренно жестких поверхностей обычно меньший единицы, тут вырастает до нескольких единиц! Причина такого неожиданного поведения вот в чем: когда соприкасаются атомы одного сорта, то они не могут «знать», что они принадлежат разным кускам меди. Будь там между ними другие атомы (атомы окислов, смазки, тонких поверхностных слоев загрязнений), тогда атомам меди было бы «ясно», находятся ли они на одном куске или на разных. Вспомните теперь, что именно из–за сил притяжения между атомами медь является твердым веществом, и вам станет понятно, почему невозможно правильно определить коэффициент трения для чистых металлов.
То же явление наблюдается в простом домашнем опыте со стеклянной пластинкой и бокалом. Поставьте бокал на пластинку, накиньте на него петлю и тяните; он неплохо скользит и коэффициент трения чувствуется; конечно, этот коэффициент слегка нерегулярен, но все же это коэффициент. Увлажните теперь пластинку и ножку бокала и потяните; вы почувствуете, что они слиплись. Внимательно вглядевшись, можно обнаружить даже царапины. Дело в том, что вода может удалять жир и прочие вещества, засоряющие поверхность; остается чистый контакт стекло – стекло. Этот контакт настолько хорош, что разорвать его не так–то просто: нарушить его трудней, чем вырвать кусочки стекла, вот и возникают царапины.
§ 3. Молекулярные силы
А теперь перейдем к характеристике молекулярных сил. Это силы, действующие между атомами; ими в конечном счете и вызывается трение. Классической физике так и не удалось удовлетворительно объяснить молекулярные силы. Чтобы их полностью понять, понадобилась квантовая механика. Эмпирически, однако, силу, действующую между двумя атомами, можно изобразить примерно так, как на фиг. 12.2, где эта сила
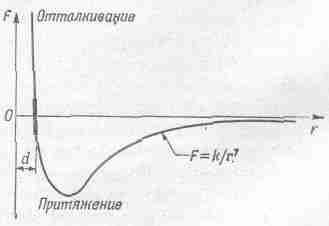 |
Бывают и другие случаи: в молекуле воды, например, отрицательные заряды размещены главным образом на атоме кислорода и центры положительных и отрицательных зарядов оказываются не в одной точке, поэтому соседние молекулы испытывают действие сравнительно больших сил. Называют эти силы
Эти молекулярные силы можно увидеть почти непосредственно и в опыте со скольжением бокала по стеклу, и в опыте с двумя тщательно отшлифованными и пригнанными плоскими поверхностями. Примером таких поверхностей могут служить плитки Иоганссона, которыми пользуются в машиностроении как стандартами для точных измерений длин. Если, прижав одну из плиток к другой, осторожно поднять верхнюю плитку, то нижняя тоже поднимется. Ее поднимут молекулярные силы, демонстрируя прямое притяжение атомов одной плитки к атомам другой.
И все же эти молекулярные силы притяжения не являются фундаментальными в том смысле, в каком фундаментально тяготение; они возникают в итоге неимоверно сложного взаимодействия всех электронов и ядер одной молекулы со всеми электронами и ядрами другой. Никакой простой формулы, которая бы учитывала все эти сложности, нельзя получить, так что это явление не фундаментальное.
Именно потому, что молекулярные силы притягивают на большом удалении и отталкивают на малом (см. фиг. 12.2), и существуют твердые тела; их атомы скреплены воедино взаимным притяжением, но держатся все же на расстоянии друг от друга (если их сблизить, сразу включается отталкивание). На том расстоянии
Когда молекулы лишь
§ 4. Фундаментальные силы. Поля
Мы хотим побеседовать теперь об оставшихся фундаментальных силах. Называем мы их фундаментальными потому, что законы их действия фундаментально просты. Сперва рассмотрим электрическую силу.
Тела несут в себе электрические заряды, которые состоят просто из электронов и протонов. Если два тела заряжены, меж ними действует электрическая сила; если величины зарядов равны соответственно
Для разноименных зарядов этот закон похож на закон тяготения, но для
1/4??0= 8,99•109
?0= 8,854•10–12
Итак, закон силы для покоящихся зарядов имеет вид
F=q1q2r/4??0r3 (12 2)
В природе самый важный из всех зарядов – это заряд отдельного электрона, он равен 1,60•10–19
Анализ фундаментальных сил (не сил трения, а электрических сил или сил тяготения) связан с интересным и очень важным понятием.
Теория этих сил намного сложнее, чем об этом следует из закона обратных квадратов. Закон этот действует лишь тогда, когда взаимодействующие тела находятся в покое. Поэтому нужен усовершенствованный метод обращения с очень сложными силами – силами, которые возникают, когда тела начинают двигаться запутанным образом. Как оказалось, для анализа сил такого типа очень полезен подход, основанный на введении понятия «поля». Чтобы пояснить мысль на примере, скажем, электрической силы, положим, что в точке
F=q1q2r/r2. (12.3)
Чтобы проанализировать эту силу при помощи понятия поля, мы говорим, что заряд q1 в точке
Е=q1r/4??0r3 . (12.4)
А затем мы пишем
F =q2E, (12.5)
т. е. связываем силу, поле и заряд в поле. В чем же суть всего этого? Суть в том, что анализ разделяется на две части. Одна часть говорит, что что–то
Да и в случае тяготения мы можем сделать то же самое. Сила теперь F
Такое разделение на две части не так уж тривиально, как могло бы показаться на первый взгляд. Оно было бы тривиальным, было бы просто иной записью того же самого, если бы законы действия сил были совсем просты, но они очень сложны, и оказывается, что поле настолько реально, что почти не зависит от объектов, создающих его. Можно колебать заряд, и влияние этого (поле) скажется на расстоянии. Если колебания прекратятся, в поле все равно будут ощущаться следы этих колебаний, потому что взаимодействие двух частиц не происходит мгновенно. Оттого и желательно уметь запоминать, что здесь раньше происходило. Если сила действия на заряд зависит от того, где другой заряд был вчера и каким он тогда был, то должна быть возможность проследить за тем, что было вчера; в этом и состоит сущность поля. Чем сложнее силы, тем реальней поле, и наша техника разделения становится все менее и менее искусственной.
Желая анализировать силы при помощи полей, мы нуждаемся в законах двоякого рода. Первые–это отклик на поле. Они дают нам уравнения движения. Например, закон отклика массы на поле тяжести состоит в том, что сила равна массе, умноженной на поле тяжести, или если тело еще и заряжено, то отклик заряда на электрическое поле равен заряду, умноженному на электрическое поле. Вторая часть анализа природы в таких положениях – это формулировка законов, определяющих напряженность поля и способ его возникновения. Эти законы иногда называют
слов.
Вот вам для начала самое замечательное свойство поля, оно абсолютно точно и легко усваивается. Общее электрическое поле, создаваемое группой источников, есть векторная сумма полей, создаваемых по отдельности первым, вторым и т. д. источниками. Иными словами, когда поле создано множеством зарядов и если отдельное поле первого есть Е1, а второго –Е2 и т. д., то мы должны просто сложить эти векторы, чтобы получить общее поле. Принцип этот выражается в виде
Е = Е1 + Е2 + Е3 + … (12.6) или, в согласии с определением поля,
 |
Можно ли эти методы применить к тяготению? Силу притяжения двух масс m1 и m
F = m2C. (12.8)
По аналогии с электричеством
 |
и тогда поле тяжести нескольких масс равно
С = С1+С2+С3+.. . (12.10)
В гл. 7, где рассматривалось движение планет, мы по существу использовали именно этот принцип. Мы складывали все векторы сил, чтобы обнаружить общую силу, действующую на планету. Разделив на ее массу, мы и получим (12.10).
Уравнения (12.6) и (12.10) выражают так называемый
С электричеством тесно связана сила другого рода, называемая магнитной; ее тоже можно анализировать через понятие поля. Некоторые из качественных связей между этими силами видны в опыте с электронной трубкой (фиг. 12.3).
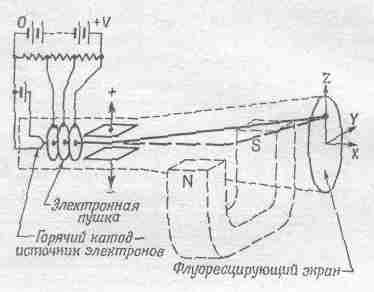 |
На одном конце трубки помещен источник, испускающий поток электронов, а внутри имеется устройство, разгоняющее электроны до большой скорости и посылающее часть их на светящийся экран на другом конце трубки. Световое пятно в центре экрана, в месте ударов электронов, позволяет проследить за их путем. На пути к экрану пучок проходит сквозь узкую щель между параллельными металлическими пластинами, расположенными, допустим, плашмя. К пластинам подведено напряжение, позволяющее любую из них заряжать отрицательно. Напряжение создает между пластинами электрическое поле.
В первой части опыта отрицательное напряжение подается на нижнюю пластину, т. е. на ней образуется избыток электронов. Одноименные заряды отталкиваются, и поэтому светящееся пятно на экране взлетает внезапно вверх. (Можно сказать и иначе: электроны «чувствуют» ноле и отвечают отклонением вверх.) Затем переключим напряжение и зарядим отрицательно уже верхнюю пластину. Световое пятно на экране опустится вниз, показывая, что электроны пучка отталкиваются электронами верхней пластины. (Иначе говоря, электроны «ответили» на изменение направления поля.)
Во второй части опыта напряжение на пластины уже не подается, а вместо этого проверяется влияние магнитного поля на электронный пучок. Для этого необходим подковообразный магнит, достаточно широкий, чтобы «оседлать» практически всю трубку. Предположим, что мы подвели магнит снизу к трубке, обхватили им ее и направили полюсы кверху (в виде буквы U). Мы замечаем, что пятно на экране смещается, скажем кверху, когда магнит приближается снизу. Выходит, что магнит отталкивает пучок. Но не так все просто: если мы перевернем магнит, не переставляя его сторон, и приблизим его к трубке сверху, то пятно снова сдвинется
Чтобы понять такое своеобразное поведение, нужно придумать какую–то иную комбинацию сил. Объясняется все это вот как. Вдоль магнита, от полюса к полюсу, тянется
Мы пока не дадим полного закона сил взаимодействия зарядов, движущихся друг относительно друга в произвольных направлениях, потому что он чересчур сложен, но зато приведем формулы для случая,
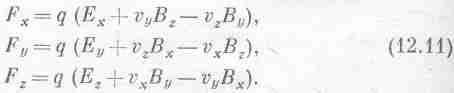 |
Если случайно магнитное поле имеет только компоненту
§5 Псевдосилы
Очередной тип сил, который нам предстоит рассмотреть, – это псевдосилы.
В гл. 11 мы обсудили взаимоотношение двух молодых людей, Джо и Мика, обладателей различных систем координат. Пусть положение частицы по измерениям Мика есть
где s показывает, насколько сместилась система Джо относительно системы Мика. Пусть у Мика в системе выполняются законы движения. Как они выглядят для Джо? Сперва мы обнаружим, что
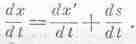 |
Раньше мы считали s постоянной и убедились, что законы движения при этом не меняются, так как
 |
но закон силы, по мнению Мика, иной:
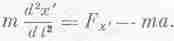 |
Иначе говоря, поскольку система координат Мика ускоряется по отношению к системе Джо, появляется добавочный член
Примером псевдо- (как бы-, вроде-) силы является хорошо известная «центробежная сила». Наблюдатель во вращающейся системе координат (во вращающемся ящике) обнаружит таинственные силы, не вызываемые ни одним из известных источников сил; они отбрасывают предметы к стенке ящика. А объясняются они просто тем, что у наблюдателя нет ньютоновой системы координат – простейшей из всех.
Псевдосилы обнаруживаются на любопытном опыте, состоящем в том, что мы толкаем с ускорением кувшин с водой по столу. Тяжесть действует на воду вниз, но из–за горизонтального ускорения есть еще и псевдосила в горизонтальном направлении, назад по отношению к ускорению. Сумма силы тяжести и псевдосилы образует угол с вертикалью, во время ускорения поверхность воды перпендикулярна к этой сумме сил, т. е. наклонена под углом к столу, и вода приподнята к задней стенке кувшина. Когда мы перестаем толкать кувшин, когда он замедляется вследствие трения, псевдосила меняет свое направление и вода приливает к передней стенке кувшина (фиг. 12.4).
 |
Фиг. 12.4. Иллюстрация к псевдосилам
Очень важным свойством псевдосил следует считать то, что они всегда пропорциональны массам; то же справедливо и для тяжести. Существует поэтому возможность, что
Эйнштейн выдвинул знаменитую гипотезу, что ускорение вызывает имитацию (подобие) тяготения, что силы ускорения (псевдосилы)
Казалось бы, ничто не мешает считать тяжесть псевдосилой, говорить, что нас прижимает вниз оттого, что нас ускоряет вверх; но как быть с жителями Новой Зеландии, на другой стороне Земли – их–то куда ускоряет? Эйнштейн понял, что тяготение можно считать псевдосилой одновременно только в одной точке; его рассуждения привели к предположению, что
Чтобы пояснить в общих чертах, как тяготение может быть результатом действия псевдосил, мы приведем чисто геометрический пример, ничего общего не имеющий с истинным положением вещей. Предположим, что мы с вами обитаем в двумерном мире и ничего о третьем измерении не знаем. Мы бы считали, что живем на плоскости, а на самом деле, предположим, жили бы на шаре; пускай теперь мы бросили предмет вдоль нашей поверхности, не действуя больше на него никакими силами. Как бы он двигался? Нам казалось бы, что он движется по прямой линии, но поскольку третьего измерения нет и он должен был бы оставаться на поверхности шара, то он двигался бы по кратчайшему расстоянию на сфере, т. е. по окружности большого круга. Бросим точно так же другой предмет, но в ином направлении; он направится тоже по дуге большого круга. Мы думаем, что находимся на плоскости, и надеемся поэтому, что расстояние между двумя предметами будет расти линейно с течением времени. Но тщательные наблюдения вдруг обнаружат, что на достаточно большом расстоянии предметы снова начнут сближаться, как если бы они притягивали друг друга. Но они
§ 6. Ядерные силы
Мы заключим эту главу кратким обзором единственных ныне известных сил, отличающихся от перечисленных, –
РАБОТА И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ (I)
§ 2. Работа, выполняемая тяжестью
§ 3, Сложение энергий
§ 4. Поле тяготения больших тел
§ 1. Работа падающего тела
В гл. 4 мы разобрали вопрос о сохранении энергии. При этом законами Ньютона мы не пользовались. Интересно теперь посмотреть, как возникает сохранение энергии из–за того, что действуют эти законы. Для ясности мы начнем с самых простых примеров и постепенно будем их усложнять.
Простейший пример сохранения энергии – это тело, падающее вниз, т. е. тело, движущееся только в вертикальном направлении. Если оно меняет свою высоту под влиянием только тяжести, то из–за движения оно обладает кинетической энергией
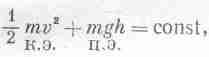 |
или
Мы хотим показать, что это утверждение правильно. Что значит доказать его правильность? Второй закон Ньютона говорит, как движется тело, как со временем изменяется его скорость (а именно, что в падении она растет пропорционально времени, а высота падения меняется как квадрат времени). Если поэтому отмерять высоту от нулевой точки (где тело покоилось), то не будет ничего странного в том, что она окажется равной квадрату скорости, умноженному на какие–то постоянные. Однако все же рассмотрим это повнимательней.
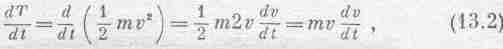 |
Попробуем вычислить
потому что
В общем случае получается F•v, но для нашего одномерного случая лучше оставить просто произведение силы на скорость.
Сила в нашем простом примере постоянна, равна –
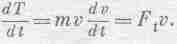 |
Мы только что показали, пользуясь Вторым законом Ньютона, что для постоянных сил энергия сохраняется, если только прибавлять потенциальную энергию
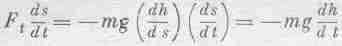 |
Скорость–это скорость изменения расстояния вдоль кривой
так что
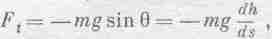 |
Чтобы точно уяснить себе, как вообще соблюдается сохранение энергии в механике, рассмотрим сейчас некоторые полезные понятия.
Во–первых, рассмотрим скорость изменения кинетической энергий в общем трехмерном случае. Кинетическая энергия, когда движение имеет три измерения, равна
Дифференцируя ее по времени, получаем три устрашающих члена:
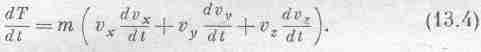 |
Но ведь
dT/dt=F•v (13.5)
А можно это вывести и быстрей: если а и b – два вектора, зависящих от времени, то производная от a•b равна
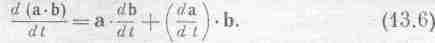 |
Подставим сюда а=b=v:
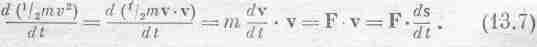 |
Так как понятие кинетической энергии и вообще энергии очень важно, то различным величинам в этих уравнениях присвоены разные имена:
А интегрируя, получаем
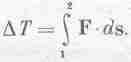 |
(13.9)
Что это значит? Это значит, что, как бы и по какой бы кривой траектории ни двигалось тело под действием силы, все равно изменение в к. э. при переходе от одной точки кривой к другой равно интегралу от компоненты силы вдоль кривой, умноженной на дифференциал смещения
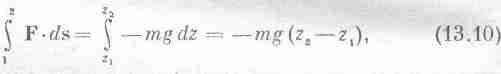 |
так что в потенциальную энергию входит только
Несколько слов о единицах. Так как сила измеряется в ньютонах, а для получения работы ее умножают на расстояние, то работу измеряют в единицах
Приведем еще несколько примеров работы и сохранения энергии. Рассмотрим тело, которое вначале имеет кинетическую энергию и быстро двигается, скользя по полу с трением. Оно останавливается. В начале кинетическая энергия
§ 2. Работа, выполняемая тяжестью
Теперь займемся задачей потруднее, когда силы уже не постоянны и не направлены вниз, как раньше. Мы рассмотрим, например, движение планеты вокруг Солнца или спутника вокруг Земли.
Сперва мы рассмотрим движение тела, которое падает из точки
 |
Будет ли в этих обстоятельствах сохраняться энергия? Единственное отличие от того, что было раньше, – что теперь сила не постоянна, она
Этот одномерный случай рассматривать легко, потому что мы знаем, что изменение кинетической энергии равно интегралу от начала движения до конца от силы –
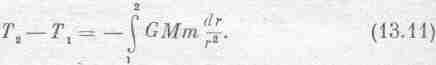 |
В формуле нет никакого косинуса, потому что сила и перемещение направлены одинаково. Интегрировать
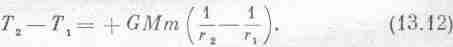 |
Перед нами другая формула для потенциальной энергии. Уравнение (13.12) говорит нам, что величина 1/2
У нас теперь есть формула для потенциальной энергии в поле тяготения для вертикального движения. Здесь возникает интересный вопрос: можно ли добиться
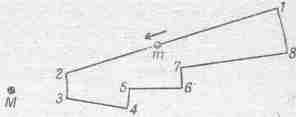 |
Мы должны доказать следующее предположение: раз трения нет, тело должно вернуться ни с меньшей, ни с большей скоростью, а как раз с такой, чтобы еще и еще делать круги по этому замкнутому пути. Или, другими словами, вся работа,
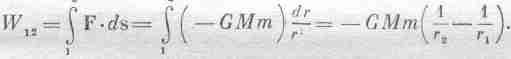 |
От
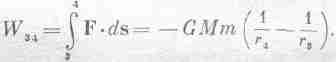 |
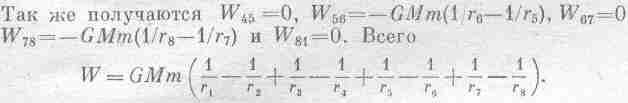 |
Но ведь r2=r3, r4=r5, r6 =r7,
Но возникает подозрение, не слишком ли эта кривая проста. А что даст
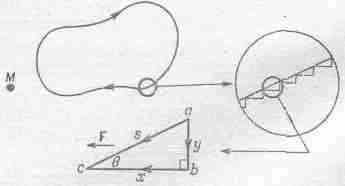 |
Показан увеличенный отрезок этого пути и близкая к нему траектория, состоящая из радиальных и круговых участков, а также один из зубцов этой траектории.
Но надо еще посмотреть, действительно ли работа обхода вокруг маленького треугольника тоже равна нулю. Увеличим один из треугольников (см. фиг. 13.4). Равны ли работы по пути от а к b и от b к с работе, совершаемой, когда идешь напрямик от а к с? Пусть сила действует в каком–то направлении. Расположим треугольник так, чтобы у его катета
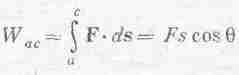 |
(поскольку сила постоянна). Теперь определим работу на двух катетах. На вертикальном катете
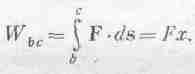 |
Мы убеждаемся таким образом, что работа обхода по бокам маленького треугольника такая же, как и по склону, потому что scos? равно
Это очень примечательный результат. Благодаря ему нам становятся известны такие подробности о движении планет, о которых мы раньше и не догадывались. Выясняется, что когда планета вертится вокруг Солнца одна, без спутников и в отсутствие каких–либо других сил, то квадрат ее скорости минус некоторая константа, деленная на расстояние до Солнца, вдоль орбиты не меняется. Например, чем ближе планета к Солнцу, тем быстрее она движется. Но насколько быстрее? А вот насколько: если вместо движения вокруг Солнца вы толкнете ее к Солнцу с той же скоростью и подождете, пока она не упадет на нужное расстояние, то приобретенная скорость будет как раз такой, какой планета обладает на этой орбите, потому что получился просто другой пример сложного пути обхода. Если планета вернется по такому пути обратно, ее кинетическая энергия окажется прежней. Поэтому независимо от того, движется ли она по настоящей невозмущенной орбите или же по сложному пути (но без трения), кинетическая энергия в момент возвращения на орбиту оказывается как раз такой, какой нужно.
Значит, когда мы проводим численный анализ движения планеты по орбите (как мы делали раньше), мы можем проверить, не сделали ли заметных ошибок при расчете этой постоянной величины, энергии, на каждом шаге; она не должна меняться. Для орбиты, приведенной в табл. 9.2 (стр. 170), энергия меняется примерно на 1,5% с начала движения до конца. Почему? То ли потому, что в численном методе мы пользовались конечными приращениями, то ли из–за мелких погрешностей в арифметике.
Рассмотрим энергию в другой задаче: задаче о массе, подвешенной на пружине. Когда отклоняют массу от положения равновесия, сила, восстанавливающая ее положение, пропорциональна смещению. Можно ли в этих условиях вывести закон сохранения энергии? Да; потому что работа, совершаемая этой силой, равна
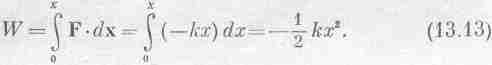 |
Значит, у массы, подвешенной на пружине, сумма кинетической энергии ее колебаний и
§ 3. Сложение энергий
Перейдем теперь к более общему случаю и рассмотрим, что произойдет, если тел много. Предположим, что имеется несколько тел; пронумеруем их: i = l, 2, 3, … и пусть все они притягивают друг друга. Что тогда произойдет? Можно доказать, что если сложить кинетические энергии всех тел и добавить сюда сумму (по всем
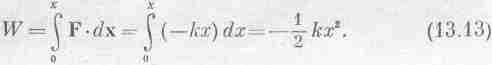 |
Как же это доказать? Мы продифференцируем обе стороны по времени и докажем, что получится нуль. При дифференцировании 1/2
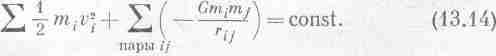 |
из закона тяготения, и увидим в конце концов, что останется как раз производная по времени от
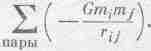 |
Начинаем доказательство. Производная кинетической энергии по времени есть
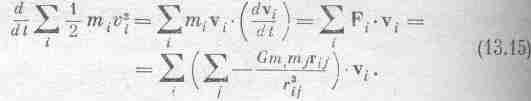 |
Производная по времени от потенциальной энергии есть
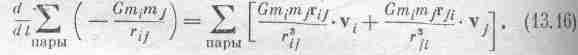 |
но
 |
так что
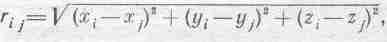 |
потому что rij=-rji, хотя rij=r
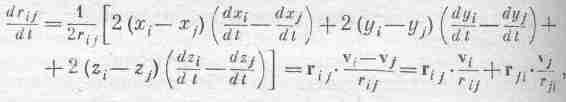 |
Теперь внимательно посмотрим, что значит
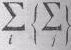 |
и
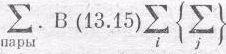 |
означает, что i принимает по порядку
все значения i=1, 2, 3,…, и для каждого
С другой стороны, в (13.16) ? означает, что каждая пара i и j встречается лишь однажды. Скажем, частицы 1 и 3 дают только один член в сумме. Чтобы отметить это, можно договориться, что
F3= F13+F2
то работа равна
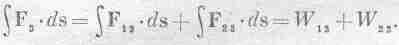 |
Стало быть, вся работа равна сумме работ, произведенных против силы 1 и против силы 2, как если бы они действовали независимо. Продолжая рассуждать таким образом, мы увидим, что полная работа, которую необходимо выполнить, чтобы собрать данную конфигурацию тел, в точности равна значению (13.14) для потенциальной энергии. Именно из–за того, что тяготение подчиняется принципу наложения сил, можно потенциальную энергию представить в виде суммы по всем парам частиц.
§ 4. Поле тяготения больших тел
Теперь рассчитаем поля, встречающиеся во многих физических задачах, когда речь идет
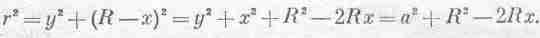 |
Но мы видим, что
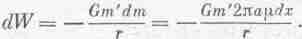 |
Значит,
или
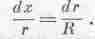 |
Поэтому
 |
и получается
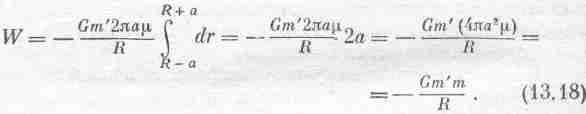 |
Стало быть, для тонкого слоя потенциальная энергия массы m
Но посмотрим, что произойдет, если точка
РАБОТА И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ (II)
§1. Работа
§2. Движение при наложенных связях
§3. Консервативные силы
§4. Неконсервативные силы
§5. Потенциалы и поля
§ 1. Работа
В предыдущей главе мы ввели много новых понятий и идей, играющих важную роль в физике. Идеи эти столь важны, что, пожалуй, стоит посвятить целую главу внимательному ознакомлению с ними. Мы не будем здесь повторять «доказательства» и красивые приемы, позволяющие просто получать важные результаты, а вместо этого сосредоточим наше внимание на обсуждении самих идей.
Штудируя любой вопрос технического характера, для понимания которого нужна математика, мы всегда сталкиваемся с необходимостью понять и отложить в памяти массу фактов и идей, объединенных определенными связями, Существование этих связей можно «доказать или «показать». Ничего не стоит спутать само доказательство с тем соотношением, которое оно устанавливает. Конечно, куда важнее выучить и запомнить не доказательство, а само соотношение. Тогда уж в любом случае мы сможем сказать: «Легко показать, что…» то–то и то–то верно, а то и действительно показать это, Приводимые доказательства почти всегда состряпаны, сфабрикованы с таким расчетом чтобы, во–первых, их легко было воспроизвести мелом на доске или пером на бумаге и, во–вторых, чтобы они выглядели поглаже. В итоге доказательство выглядит обманчиво просто, хотя, быть может, на самом деле автор много часов искал разные пути расчета, пока не нашел самый изящный – тот, который приводит к результату за кратчайшее время! Глядя на вывод формулы, надо вспоминать не этот вывод, а скорее сам факт, что то–то и то–то
Ни одно из доказательств, приведенных в этом курсе, автор не запомнил с тех времен, когда сам учил физику. Наоборот, он просто вспоминает, что то–то является верным, и, пытаясь пояснить, как это доказывается, сам придумывает доказательство в тот момент, когда оно необходимо. И всякий, кто действительно изучил предмет, должен быть в состоянии поступать так же, не запоминая доказательств. Вот почему в этой главе мы будем избегать вывода различных положений, сделанных ранее, а просто будем подводить итоги.
Первая идея, которую нужно будет переварить, – это то, что
Физическая работа выражается в виде ?F•ds, или «контурный интеграл от F по
Очевидно, что сила, направленная под прямым углом к перемещению, никакой работы не произведет.
Если, далее, вектор смещения ?s разложить на составляющие, т. е. если истинное смещение есть ?s и мы хотим считать, что оно состоит из составляющих смещения ?x; в направлении
Все, что мы только что сказали, содержится в формуле
совсем другое – понять ее смысл и ее следствия.
Смысл слова «работа» в физике настолько отличается от того, что подразумевают под этим словом в обычных обстоятельствах, что надо тщательно проследить это различие. Например, по точному смыслу физического определения работы, если вы держите в руках двухпудовую гирю, вы не совершаете никакой работы. Вас бросает в пот, ваши руки дрожат, вы дышите тяжело, как будто взбежали по лестнице, а работы вы не совершаете. Когда вы взбегаете по лестнице, то считается, что вы
Когда вы держите груз, вы, конечно, выполняете «физиологическую» работу. Отчего вас бросает в пот? Почему для такого занятия вам необходимо хорошо питаться? Почему все механизмы внутри вас работают в полную силу, когда вы подставили спину под груз? Ведь можно на этот груз не тратить никаких усилий, стоит лишь положить его на стол, и стол спокойно и мирно, не нуждаясь ни в какой энергии, будет держать себе тот же груз на той же высоте! Физиология дает примерно следующее объяснение. У человека и у других животных есть два рода мышц. Одни, называемые
Но вернемся к физике и зададим еще один вопрос:
§ 2. Движение при наложенных связях
Силы и работа обладают еще одним интересным свойством. Пусть имеется некоторый уклон, какая–то криволинейная колея, по которой частица должна двигаться без трения. Или имеется маятник – груз на ниточке; нить маятника вынуждает груз двигаться по кругу вокруг точки подвеса. Намотав нить на колышек, можно в качании менять точку подвеса, так что траектория груза будет складываться из двух окружностей разного радиуса. Все это примеры так называемых
В движении с неподвижными связями без трения эти связи не производят никакой работы, потому что реакции связей всегда прилагаются к телу под прямым углом к самим связям; так обстоит дело и с реакцией колеи и с натяжением нити.
Силы, возникающие при движении частицы вниз по склону под действием тяжести, весьма и весьма запутаны: здесь и реакции связи, и сила тяжести, и т. п. И все же, если основывать свои расчеты движения лишь на сохранении энергии и на учете
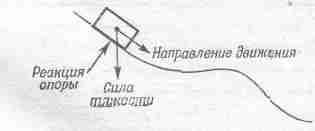 |
Важное свойство сил, о котором мы говорили, состоит в том, что если силу можно разбить на две или несколько «частей», то работа, выполняемая самой силой при движении по некоторой кривой, равна сумме работ, произведенных каждой «частью» силы. Если мы представляем силу в виде векторной суммы нескольких сил (силы тяжести, реакции связей и т. д., или x–составляющих всех сил плюс y–составляющие и т.д., или еще как–нибудь), то работа всей силы равна сумме работ тех частей, на которые мы ее разделили.
§ 3. Консервативные силы
В природе существуют силы, скажем сила тяжести, обладающие замечательным свойством – «консервативностью» (никаких политических идей, ничего двусмысленного в этом понятии нет). Когда мы подсчитываем, какую работу выполняет сила, двигая тело от одной точки к другой, то вообще работа зависит от траектории; но в особых случаях эта зависимость пропадает. Если работа не зависит от траектории, мы говорим, что сила консервативна. Иными словами, если интеграл от произведения силы на приращения смещений между точками
Чтобы доказать это, рассмотрим фиг. 14.2.
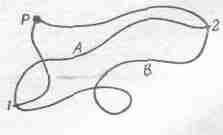 |
Фиксируем произвольную точку
Обозначим эту функцию положения через–
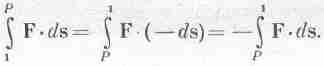 |
Значит, работа на участке
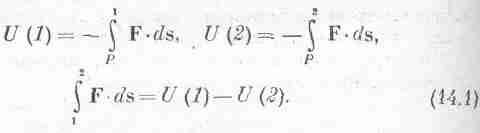 |
Величина
Итак, у нас имеются два утверждения: 1) работа, выполняемая силой, равна изменению кинетической энергии системы, но 2) математически для консервативных сил выполненная работа равна минус изменению функции
T+U=const. (14.2)
Рассмотрим формулу потенциальной энергии для ряда случаев. Если поле тяготения однородно, если мы не поднимаемся до высот, сравнимых с радиусом Земли, то сила постоянна и направлена вертикально, а работа равна просто произведению силы на расстояние по вертикали. Стало быть,
и за точку
Энергия, необходимая для сжатия пружины на расстояние
и нуль потенциальной энергии приходится на точку
Потенциальная энергия тяготения точечных масс M и m на расстоянии r друг от друга равна
Константа здесь выбрана так, чтобы потенциал исчезал на бесконечности. Конечно, эту
Давайте теперь поработаем с одной из этих формул, посмотрим, поняли ли мы их смысл.
С какой скоростью должен двигаться искусственный спутник, чтобы не падать на Землю? Мы когда–то решали эту задачу и получили
Продолжим теперь наш обзор характеристик потенциальной энергии. Давайте рассмотрим взаимодействие двух молекул или двух атомов, например двух атомов кислорода. Когда они находятся далеко друг от друга, они притягиваются с силой, обратно пропорциональной седьмой степени расстояния, а при тесном сближении они сильно отталкиваются. Проинтегрировав минус седьмую степень расстояния, чтобы получить работу, мы увидим, что потенциальная энергия
Если мы чертим некую кривую потенциальной энергии
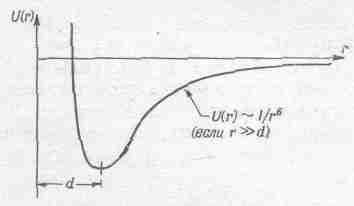 |
Минимум потенциальной энергии в точке r=
Почему мы говорим о потенциальной энергии? Потому что идея
Заметим еще, что, когда на тело одновременно действуют несколько консервативных сил, потенциальная энергия тела есть сумма потенциальных энергий от каждой силы. Это то, что мы утверждали и раньше, потому что, когда сила представляется векторной суммой сил, работа, производимая ею, равна сумме работ, производимых отдельными силами; поэтому ее можно представить как изменения потенциальных энергий от каждой силы по отдельности. Значит, общая потенциальная энергия равна сумме всех частей.
Мы можем обобщить это на случай системы многих тел, как, например, Юпитера, Сатурна, Урана и т. д. или атомов кислорода, азота, углерода и т. д., взаимодействующих друг с другом попарно, причем силы взаимодействия каждой пары консервативны. В таких условиях кинетическая энергия всей системы есть просто сумма кинетических энергий всех отдельных атомов, или планет, или частиц, а потенциальная энергия системы есть сумма потенциальных энергий взаимодействия отдельных пар, рассчитанных в предположении, что других частиц нет. (На самом деле для молекулярных сил это неверно, и формула получается несколько сложнее; для ньютонова тяготения это определенно справедливо, а для молекулярных сил годится лишь как приближение. Можно, конечно, говорить о потенциальной энергии молекулярных сил, но она иногда оказывается более сложной функцией положений атомов, чем простая сумма попарных взаимодействий.) Поэтому потенциальная энергия в частном случае тяготения представляется суммой по всем парам
§ 4. Неконсервативные силы
Мы потратили немало времени, обсуждая свойства консервативных сил. Что же мы теперь скажем о неконсервативных силах? Мы хотим разобраться в этом вопросе более подробно, чем это обыкновенно делают, и показать, что неконсервативных сил не бывает! Оказывается, все основные силы природы, по–видимому, консервативны. Не подумайте, что это следствие из законов Ньютона. На самом деле, насколько представлял себе это сам Ньютон, силы могут быть неконсервативными, как, например, трение, которое кажется неконсервативным. Употребляя слово «кажется», мы проводим современную точку зрения, которая доказывает, что все глубинные силы, все силы взаимодействия между частицами на самом фундаментальном уровне суть силы консервативные.
Когда мы, например, анализируем систему наподобие большого шарового звездного скопления (фотографию такого скопления мы показывали) с тысячами взаимодействующих звезд, то формула для общей потенциальной энергии состоит просто из суммы слагаемых, каждое из которых выражает взаимодействие какой–то пары звезд; точно так же и кинетическая энергия есть сумма кинетических энергий всех отдельных звезд. Но шаровое скопление как целое движется и в пространстве, и окажись мы от него так далеко, что не смогли бы различать отдельных деталей, мы бы приняли его за единый предмет. Если бы при этом к нему были приложены какие–то силы, то часть из них могла бы двигать его как целое и мы бы увидели, как центр этого тела движется. С другой стороны, прочие силы могли бы, если так можно выразиться, «тратиться» на повышение потенциальной или кинетической энергии «частиц» внутри «тела». Положим, например, что действие этих сил привело бы к расширению всего скопления и увеличению скоростей «частиц». Общая энергия «тела» на самом деле сохранялась бы. Но, глядя издалека нашими слабыми глазами, не различающими беспорядочных внутренних движений, мы бы видели только кинетическую энергию всего тела и нам бы казалось, что энергия не сохраняется, хотя все дело было бы в том, что мы не различаем деталей. Оказывается, что это всегда так: общая энергия Вселенной, кинетическая плюс потенциальная, если как следует посмотреть, всегда постоянна.
Изучая тончайшие свойства вещества на атомном уровне,
В качестве другого примера возьмем трение. Неверно, что кинетическая энергия в результате трения исчезает; это неверно, хотя скользящее тело и впрямь останавливается и кажется, что кинетическая энергия пропала. Но она не пропадает, ибо атомы внутри тела начинают двигаться с большим запасом кинетической энергии; хоть мы этого и не можем увидеть, но можно догадаться об этом по повышению температуры. Конечно, если не обращать внимания на тепловую энергию, то теорема о сохранении энергии покажется неправильной.
Еще в одном случае может показаться, что энергия не сохраняется: когда мы изучаем часть всей системы. Вполне естественно, что если что–то взаимодействует с чем–то внешним и мы пренебрегаем этим взаимодействием, то теорема о сохранении энергии будет выглядеть неверной.
В классической физике в потенциальную энергию включались только тяготение и электричество, но теперь у нас есть и атомная энергия и многое другое. В классической теории, например, свет – это особая форма энергии, но можно, если нам этого хочется, представить себе энергию света как кинетическую энергию фотонов, и тогда наша формула (14.2) опять окажется справедливой.
§ 5. Потенциалы и поля
Теперь обратимся к некоторым идеям, связанным с потенциальной энергией и с понятием
F = mC.
Тяготение можно анализировать, считая, что в каждом месте пространства имеется вектор С, который «действует» на массу, помещенную в это место, но который присутствует там безотносительно к тому, поместили ли мы туда массу или нет. Вектор С имеет три составляющие, и каждая из них является функцией от
С потенциальной энергией можно сделать то же самое. Так как потенциальная энергия, интеграл от (Сила)•(ds), может быть записана в виде массы m, умноженной на интеграл от (Поле)•(ds) – это простое изменение масштаба, – то потенциальную энергию
— ?
масштабом:
U= -?F•ds=-m?C•ds=m?. (14.7)
Зная в каждой точке пространства эту функцию ?
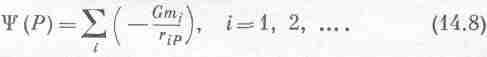 |
Этой формулой, представляющей потенциал в виде суммы потенциалов отдельных масс, мы пользовались в предыдущей главе, чтобы вычислить потенциал сферического слоя (мы тогда сложили потенциалы всех поясков, на какие был нарезан слой). Итог расчета показан на фиг. 14.4.
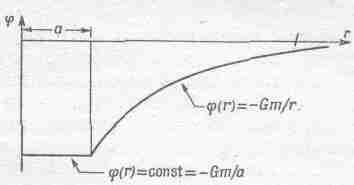 |
Потенциал отрицателен, равен нулю на бесконечности, падает как 1/r, пока r не станет равным
В этих рассуждениях кроется ключ к вычислению силы или напряженности поля, когда потенциальная энергия известна.
Пусть потенциальная энергия тела в точке
?
Мы просто применили формулу ?F•ds=-?U для
Fx=-?u/?x. (14.10)
Конечно, это не совсем точно. На самом деле нам нужно перейти в (14.10) к пределу при ?x, стремящемся к нулю, потому что (14.10)
Итак, мы обнаруживаем, что сила в направлении
Fx
Точно так же и сила в направлении
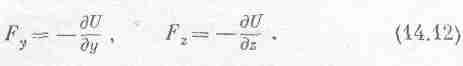 |
В этом и состоит способ получать силу из потенциальной энергии.
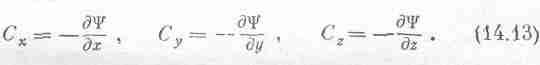 |
Заметим, кстати, что существует и другое обозначение (впрочем, пока оно нам не понадобится). Так как С есть вектор с компонентами
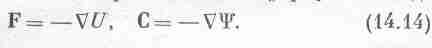 |
Глядя на ?; мы мгновенно узнаем, что наши уравнения векторные; но на самом деле уравнение (14.14) означает в точности то же, что и (14.11) и (14.12); просто это другой способ записи. Не желая писать каждый раз три уравнения, мы пишем одно лишь ?
Еще один пример полей и потенциалов связан с электричеством. В этом случае сила, действующая на неподвижное тело, равна заряду, умноженному на поле: F = qЕ. (В x–составляющую силы входят, вообще говоря, и члены, которые зависят от магнитного поля. Но из уравнения (12.10) легко увидеть, что сила, действующая на частицу со стороны магнитных полей, всегда направлена поперек поля и поперек ее скорости. Благодаря этому свойству магнетизм
?(r) = -
В качестве примера рассмотрим две параллельные металлические пластины с поверхностным зарядом ?? (на единицу площади) каждая. Такая штука называется плоским конденсатором. Мы уж убедились раньше, что снаружи пластин сила равна нулю, а между ними существует постоянное электрическое поле. Оно направлено от плюса к минусу и равно ?/?0 (фиг. 14.5).
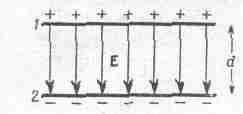 |
Мы хотим знать, какую работу надо совершить, чтобы перенести заряд от одной пластины к другой. Работа равна интегралу от
W=?F•ds= q(?1-?2).
Интеграл здесь легко вычислить, так как сила постоянна, и если обозначить толщину конденсатора
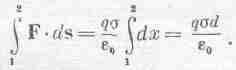 |
Разница в потенциалах ??= ?
(support [a t] reallib.org)