"Невероятно – не факт" - читать интересную книгу автора (Китайгородский Александр Исаакович)
Математик спешит на свидание
– Ты не забыл, что завтра мы идем в консерваторию?
– Ну конечно, нет.
– Заедешь за мной?
– Дел невпроворот. Давай мне билет, я приду один.
– Вот так всегда. Опять подруги надо мной посмеются. Завела, скажут, кавалера, который с тобою и показаться не желает.
– Ну ладно, давай встретимся. Где?
– У входа в продуктовый, что поближе к Никитским воротам.
– Так это на другой стороне улицы.
– Конечно. Мне не хочется, чтобы видели, как я тебя жду.
– Неизвестно, кто кого будет ждать… Но знаешь, завтра мне и правда время рассчитать трудно. От 18.00 до 19.00 я буду на месте как штык, а точнее – не скажу.
– Выходит, я час тебя буду ждать?
– Я и говорю: встретимся на месте.
– Не хочу.
– Тогда предлагаю компромиссное решение. Оба приходим между 17.40 и 18.40. И ждем не более двадцати минут.
– А если ты придешь в 18.00, а я в 18.30?
– Значит, я буду уже в зале.
– Да так мы никогда не встретимся на улице.
– Вероятность встречи довольно значительная. Хочешь, подсчитаю?
– Да не берись за карандаш, горе ты мое. И надо было влюбиться в математика…
Я, конечно, был бы рад продолжить рассказ о радостях и горестях влюбленных математика и девушки, далекой от чисел и интегралов. Тут бездна интересных психологических моментов. Но увы! Тема книги вынуждает вернуться к «сухой» науке.
Как же действительно подсчитать вероятность встречи математика с его любимой? Мы уже выяснили, что вероятность – это отношение числа благоприятных случаев к общему числу событий. А здесь как быть? Ведь встреча может состояться или не состояться в любой момент часового интервала.
Благоприятным исходом рассматриваемой задачи является мгновение встречи. Но мгновений бесконечно много. Ведь часовой интервал я могу разбить на минуты, на секунды и даже на микросекунды. Значит, здесь бесконечное число исходов, а не два, как в опыте с монетой, и не шесть, как в опыте с кубиком (игральной костью). Как же определяются вероятности в задачах такого рода? Оказывается, геометрическим путем. А поскольку геометрия требует наглядности, нам придется прибегнуть к нехитрому рисунку.
Отложим по горизонтали время прибытия девушки на свидание. На вертикальной прямой отметим минуты появления нашего героя. Если бы не было условия – ждать не более двадцати минут, то встреча могла бы произойти в любой точке квадрата, обнимающего часовые ожидания. При наличии же дополнительного условия моменты встречи попадут в заштрихованную область. Пожалуйста, проверяйте.
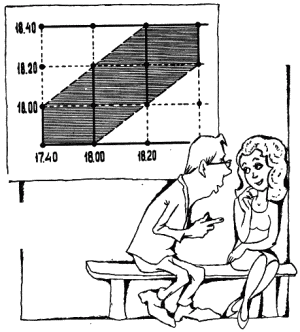 |
Девушка пришла без двадцати шесть. Встреча состоится, если кавалер явится до шести. Этому соответствует первый отрезок.
Девушка пришла в 18.00. Встреча состоится, если кавалер явится от 17.40 до 18.20. Такой встречи соответствует второй отрезок, построенный на рисунке.
Если девушка пришла в 18.20, то встреча состоится при условии, если математик явится к продуктовому магазину между 18.00 часами и крайним сроком – 18.40. Вот вам третий отрезок.
Теперь еще одна точка, и заштрихованная область будет готова: девушка успела прибежать на свидание в 18.40. Она застанет своего возлюбленного, если он явился не раньше 18.20.
Что же дальше? Где же искомая вероятность? Нетрудно догадаться, что она будет равняться частному от деления площади заштрихованной области на площадь всего квадрата.
По сути дела, определение вероятности остается тем же – благоприятные варианты относятся ко всем возможным. Но если ранее мерой было число случаев, то теперь мерой является площадь на графике.
Два незаштрихованных треугольника образуют квадрат со стороной, соответствующей 40 минутам. Его площадь 402. Таким образом, искомую вероятность получим, поделив (3600-1600) на 3600. Итого 5/9.
Будем надеяться, что математик встретится со своей девушкой.
Применение теории вероятностей к событиям с непрерывным рядом исходов намного расширяет ее возможности.
Одной из исторически первых задач такого рода была проблема, поставленная и решенная французским естествоиспытателем XVIII века Бюффоном.
На большом листе бумаги начерчен ряд параллельных линий. Наобум бросается игла, длина которой много меньше расстояния между линиями на бумаге. Игла может пересечь одну из линий, а может очутиться и между линиями. Надо оценить вероятность того, что пересечение произойдет.
Предполагается, что центр иглы с равной вероятностью может попасть в любое место бумажного листа. Так же точно считается, что угол наклона иглы к начерченным линиям может принять какое угодно значение. Если игла попадет на середину между линиями, то она не пересечет линии, как бы она ни оказалась повернутой. Если же центр иглы очутился вблизи линии, то пересечение не произойдет, если игла установится параллельно линии или около того, и напротив, игла пересечет линию, если образует угол, близкий к прямому. Получается так: чем ближе к линии попадет центр иглы, тем больше вероятность ее пересечения.
Задача может быть решена без всякой математики. Попробуйте свои силы.
| © 2025 Библиотека RealLib.org (support [a t] reallib.org) |