"Логическая игра" - читать интересную книгу автора (Кэрролл Льюис)

2. Силлогизмы

Предположим теперь, что мы разделили наш «Мир предметов» тремя способами в соответствии с тремя различными признаками. Из трех признаков можно составить три различные пары (например, если имеются признаки a, b, c, то из них можно составить три пары ab, ac и bc). Предположим кроме того, что два суждения, содержащие две из трех пар признаков, нам даны, и что из них мы умеем выводить третье суждение, содержащее оставшуюся (третью) пару признаков. (Пусть, например, мы разделили наш «Мир» в соответствии с признаками m, x и y. Тогда, если нам даны два суждения «Ни одно m не есть x'» и «Все m' суть y», содержащее пары признаков mx и my, то, опираясь на них, мы можем доказать третье суждение, содержащее признаки x и y.)

В этом случае те суждения, которые даны, называются посылками, третье, выводимое из них суждение — заключением, а все вместе — силлогизмом.

Ясно, что либо один из признаков непременно должен входить в обе посылки, либо в одну посылку должен входить сам признак, а в другую — ему противоположный.

В первом случае термин, который повторяется дважды (например, когда в качестве посылок выбраны суждения «Некоторые m суть x» и «Ни одно m не есть y'»), называется средним термином, поскольку он служит своего рода связующим звеном между двумя другими терминами.

Во втором случае (например, когда посылки имеют вид суждений «Ни один m не есть x'», и «Все m' суть y») два термина, содержащие противоположные признаки, можно назвать средними терминами.

Таким образом, в первом случае средний термин — это класс «m-предметов», во втором случае в роли средних терминов выступают два класса — «m-предметов» и «m'-предметов».

Признак, входящий в средний член или в средние члены, не входит в заключение. О нем говорят, что его «исключили» (по-ученому, «элиминировали»), что означает буквально «выставили за дверь».

Попытаемся вывести заключение из двух посылок:

«Некоторые свежие булочки неполезные»,

«Ни одна вкусная булочка не неполезная».

Чтобы выразить их с помощью фишек, необходимо разделить булочки тремя различными способами: по тому, свежие ли они, вкусные или полезные. Для этого нам придется воспользоваться большой диаграммой, условившись заранее, что x означает «свежие», y — «вкусные» и m — «полезные». (Все, что находится внутри центрального квадрата, по предположению обладает признаком m, все, что находится вне его, — признаком m', т. е. «не-m».)

В качестве m лучше всего выбрать признак, входящий в средний термин или в средние термины. (Я обозначил этот признак буквой m потому, что именно с нее начинается слово middle — «средний».)

Изображая на диаграмме посылки силлогизма, лучше всего начинать с отрицательной посылки («Ни один…» и т. д.). Дело в том, что расстановка черных фишек не вызывает никаких сомнений и помогает уточнить расположение красных фишек, которые иногда испытывают легкую неуверенность относительно того, где их присутствие наиболее желательно.

Изобразим, например, суждение «Ни одна вкусная булочка не есть неполезная (булочка)», т. е. «Ни одна y-булочка не есть m'-булочка». Оно говорит нам, что ни одна из булочек, находящихся на половине y подноса, не находится в его клетках m' (т. е. «уголках», лежащих вне центрального квадрата). Следовательно, обе клетки — m'-клетка 9 и клетка 15 — пусты, и на каждую из них мы должны поставить по черной фишке:

Нам осталось изобразить на диаграмме вторую посылку, а именно: «Некоторые свежие булочки суть неполезные (булочки)», т. е. «Некоторые x-булочки суть m' (булочки)». Последняя форма суждения говорит нам, что некоторые из булочек, находящихся на половине x нашего подноса, разместились в его клетках, помеченных буквой m'. Следовательно, одна из этих двух клеток — 9 или 10 — занята. Поскольку нам неизвестно, на какую из двух клеток следует поставить красную фишку, мы, следуя обычному правилу, должны были бы поставить ее на границу, разделяющую клетки-«соперницы». Однако в данном случае первая посылка позволяет решить спор: в ней говорится, что клетка 9 пуста. Следовательно, у красной фишки нет выбора. Волей-неволей ей приходится отправиться на клетку 10:

Какие сведения можно извлечь из этой диаграммы, чтобы с их помощью расставить фишки на малой диаграмме и, исключив признак m, получить суждение, содержащее только признаки x и y? Рассмотрим по очереди все четыре клетки малой диаграммы.

Начнем с клетки 5. Все, что мы о ней знаем, сводится к следующему: та часть большой диаграммы, которая расположена вне ее, пуста. О том, что находится внутри этой клетки, ничего не известно. Следовательно, квадрат 5 может быть и пустым, и занятым. Какая из этих возможностей соответствует действительности, сказать трудно. Поэтому мы и не осмелимся поставить на клетку 5 ни красную, ни черную фишку.

Что можно сказать о клетке 6? Здесь положение немного лучше. Ведь мы уже знаем, что в «уголке», примыкающем извне к этой клетке, что-то есть. Следовательно, на клетке 10 большой диаграммы стоит красная фишка. Правда, нам неизвестно, пуста или занята сама клетка 6, но какое это имеет значение? Одной-единственной булочки в углу квадрата совершенно достаточно, чтобы мы имели право сказать: «Этот квадрат занят» и поставить на него красную фишку.

При рассмотрении клетки 7 мы оказываемся в том же положении, как и рассмотрении клетки 5: мы знаем, что она частично пуста, но не знаем, пуст или занят примыкающий к ней извне «уголок». Таким образом, на эту клетку мы также не можем поставить ни красную, ни черную фишку.

Относительно клетки 8 нам вообще ничего не известно.

Каков же результат? Он показан на диаграмме:

Наше «заключение» необходимо извлечь из весьма скудного обрывка сведений — из того лишь факта, что в квадрате xy' стоит красная фишка. Так мы приходим к суждению «Некоторые x суть y'», т. е. «Некоторые свежие булочки (суть) невкусные (булочки)», или, если вы предпочитаете выбрать в качестве субъекта y', «Некоторые невкусные булочки (суть) свежие (булочки)» (первое звучит все-таки более обнадеживающе).

Запишем теперь силлогизм полностью. Условимся ставить после посылок горизонтальную черту (означающую «следовательно») и опускать для краткости слово «булочки», стоящее в конце каждой посылки. У нас получится следующее:

«Некоторые свежие булочки неполезные».

«Ни одна вкусная булочка не неполезная».

—

«Некоторые свежие булочки невкусные».

Вот вы и решили (надо сказать, весьма успешно) свой первый силлогизм. Позвольте поздравить вас и выразить надежду, что это всего лишь начало длинной и славной серии аналогичных побед!

Попробуем теперь решить еще один силлогизм, гораздо более трудный, чем первый, после чего вы спокойно сможете играть в «Логическую игру» либо сами с собой, либо (что предпочтительнее) с приятелем, которому эта забава придется по вкусу.

Посмотрим, какое заключение можно вывести из двух посылок:

«Все драконы не лукавые».

«Все шотландцы лукавые».

Имейте в виду: я отнюдь не гарантирую, что посылки силлогизма выражают реальные факты. Во-первых, мне никогда не приходилось видеть дракона. Во-вторых, для нас, логиков, не имеет ни малейшего значения, истинны или ложны наши посылки: все, что мы должны уметь делать, — это решать, приводят ли они логически к определенному заключению. Иначе говоря, мы должны уметь доказывать, что если бы посылки истинными, то и заключение также долждно было бы быть истинным.

Как видите, настала пора отказаться от булочек, и поднос перестал быть для нас полезным. В качестве «Мира» мы должны выбрать какой-то класс предметов, включающий в себя шотландцев и драконов. Может быть, такие предметы имеет смысл назвать «существами»? Поскольку «лукавые», очевидно, является признаком, входящим в средние члены, мы выберем следующие обозначения: m=«лукавые», x=«драконы», и y=«шотландцы». Записанные полностью, наши посылки примут следующий вид:

«Все существа — драконы — нелукавые (существа)».

«Все существа — шотландцы — лукавые (существа)».

Подставляя вместо слов буквенные обозначения, получаем:

«Все x суть m'».

«Все y суть m».

Первая посылка, как вы уже знаете, состоит из двух частей:

«Некоторые x суть m'»

и

«Ни один x не есть m».

Вторая посылка также состоит из двух частей:

«Некоторые y суть m»

и

«Ни один y не есть m'».

Начнем с отрицательных частей обеих посылок, т. е. представим с помощью большой диаграммы, во-первых, суждение «Ни один x не есть m» и, во-вторых, суждение «Ни один y не есть m'». Думаю, вам не нужно объяснять, почему этим суждениям (в отдельности) соответствуют диаграммы

и что, взятые вместе, эти диаграммы образуют одну диаграмму

Осталось изобразить на полученной диаграмме две утвердительные части посылок — «Некоторые x суть m'» и «Некоторые y суть m».

Единственные две клетки большой диаграммы, в которых могут находиться предметы, обладающие признаками xm', — это «уголки» 9 и 10. Относительно клетки 9 уже известно, что она пуста. Следовательно, красную фишку мы должны поставить на «уголок» 10.

Аналогично предметы с признаками ym могут находиться лишь в клетках 11 и 13. В клетке 11 уже стоит черная фишка — клетка пуста. Следовательно, красную фишку необходимо поставить на клетку 13.

Окончательный результат — диаграмма

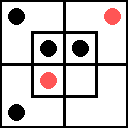А что из представленных здесь сведений можно использовать при построении малой диаграммы?

Рассмотрим по порядку все четыре клетки малой диаграммы.

Клетка 5. Мы видим, что она полностью пуста (и поэтому ставим на нее черную фишку).

Клетка 6. Эта клетка занята (ее мы отметим красной фишкой).

Клетка 7. То же самое.

Клетка 8. Относительно этой клетки никаких сведений у нас нет.

Итак, малая диаграмма заполнена весьма щедро:

А какое заключение можно вывести отсюда? Одно суждение просто не в состоянии вместить столь богатую информацию, нам придется уступить и согласиться на этот раз на два суждения.

Выбрав в качестве субъекта x, мы получим первое суждение: «Все x суть y'», т. е. «Все драконы не шотландцы».

Выбрав в качестве субъекта y, мы получим второе суждение: «Все y суть x'», т. е. «Все шотландцы не драконы».

Запишем теперь весь силлогизм полностью: и две наши посылки, и оба наших заключения. Вот что у нас получится:

«Все драконые не лукавые».

«Все шотландцы лукавые».

—

«Все драконы не шотландцы».

«Все шотландцы не драконы».

На прощание я хотел бы сделать одно важное замечание. В некоторых книгах по логике вообще не предполагается, что какой-то предмет существует. Суждение «Некоторые x суть y» в таких книгах понимается так: «Признаки x и y совместимы, в силу чего некий предмет может одновременно обладать ими обоими». Суждение же «Ни один x не есть y» они интерпретируют как несовместимость признаков x и y, в силу которой ни один предмет не может обладать ими обоими.

Суждения в таких трактатах имеют совсем иной смысл, чем тот, который они имеют в нашей «Логической игре», и будет небесполезно, если мы ясно поймем, в чем именно состоит различие.

Прежде всего рассмотрим суждение «Некоторые x суть y». Мы считаем, что связка «суть» означает «являются в действительности, на самом деле, фактически». Отсюда, разумеется, следует, что некоторые x-предметы существуют. Они же (авторы упоминавшихся книг по логике) считают, что связка «суть» означает «может быть». Из такого понимания связки никакого существования уже не следует. Таким образом, их интепретация связки `уже, чем наша: наша интерпретация включает в себя их интерпретацию (из того, что «Некоторые x суть y», следует, что «Некоторые x могут быть y»), но не наоборот. Например, согласно этим авторам, суждение «Некоторые уэлльские гиппопотамы неуклюжие» истинно (поскольку признаки «уэлльский» и «неуклюжий» совместимы в гиппопотаме), но в нашей игре оно ложно (ибо уэлльские гиппопотамы, которые должны быть неуклюжими, не существуют в природе).

Рассмотрим, далее, суждение «Ни один x не есть y». В этом случае мы понимаем связку «есть» лишь как «является в действительности», из чего вовсе не следует, что ни один x не может быть y. Они же понимают это суждение в том смысле, что ни один x не только не есть y, но и не может быть y. В данном случае они понимают суждение шире, чем мы: их интерпретация включает в себя нашу (из того, что ни один x не может быть y, следует, что ни один x не есть y), но не наоборот. Например, суждение «ни один полисмен не имеет восьми футов росту» было бы истинно в нашей игре (поскольку столь великолепные образчики полисменов покуда еще не найдены), но ложно в смысле упомянутых мною авторов. (Действительно, признаки «быть полицейским» и «иметь восемь футов росту» вполне совместимы: ничто не мешает полицейскому вырасти до указанной высоты. Необходимо лишь усердно натираться «Роуландовским макасарским маслом». Говорят, что если натирать этим маслом волосы, то волосы начинают расти. Следовательно, если натирать этим маслом полисмена, то полисмен также начнет расти.)

Рассмотрим, наконец, суждение «Все x суть y», состоящее из двух частных суждений: «Некоторые x суть y» и «Ни один x не есть y». В этом случае авторы уже упоминавшихся трудов по логике понимают связку `уже, чем мы, в первой части и шире, чем мы, — во второй. Узость интерпретации одного суждения (и у нас, и у них) отнюдь не компенсируется широтой интерпретации другого: если уж вас угораздило сбить печную трубу, то хозяин дома вряд ли утешится тем, что вы пристроите еще одну ступеньку к крыльцу.

Предложенная мной система позволит вам без особого труда решать и силлогизм в интерпретации авторов ученых трудов по логике: стоит лишь заменить «суть» на «могут быть», и все остальное пойдет как по маслу. Суждение «Некоторые x суть y» перейдет при этом в суждение «Некоторые x могут быть y», т. е. «Признаки x и y совместимы». Суждение «Ни один x не есть y» примет вид «Ни один x не может быть y», т. е. «Признаки x и y несовместимы». Суждение же «Все x суть y» станет двойным суждением «Некоторые x могут быть y, и ни один x не может быть y'», т. е. «Признаки x и y совместимы, и признаки x и y' несовместимы». При пользовании диаграммой по этой системе необходимо не упускать из виду, что красная фишка означает суждение «Вполне возможно, что в этой клетке что-нибудь есть», а черная — суждение «Вполне возможно, что в этой клетке ничего нет».