"Занимательная физика. Книга 2" - читать интересную книгу автора (Перельман Яков Исидорович)

Глава шестая Свойства жидкостей и газов.

Такое море существует в стране, известной человечеству с древнейших времен. Это знаменитое Мертвое море Палестины. Воды его необыкновенно солены, настолько, что в них не может жить ни одно живое существо. Знойный, без дождей климат Палестины вызывает сильное испарение воды с поверхности моря. Но испаряется только чистая вода, растворенные же соли остаются в море и увеличивают соленость воды Вот почему вода Мертвого моря содержит не 2 или 3 процента соли (по весу), как большинство морей и океанов, а 27 и более процентов; с глубиной соленость растет. Итак, четвертую часть содержимого Мертвого моря составляют соли, растворенные в его воде. Общее количество солей в нем оценивается в 40 миллионов тонн.

Высокая соленость Мертвого моря обусловливает одну его особенность: вода этого моря значительно тяжелее обыкновенной морской воды. Утонуть в такой тяжелой жидкости нельзя: человеческое тело легче ее.

Вес нашего тела заметно меньше веса равного объема густо-соленой воды и, следовательно, по закону плавания, человек не может в Мертвом море потонуть; он всплывает в нем, как всплывает в соленой воде куриное яйцо (которое в пресной тонет)

Юморист Марк Твен, посетивший это озеро-море, с комичной обстоятельностью описывает необычайные ощущения, которые он и его спутники испытали, купаясь в тяжелых водах Мертвого моря:

«Это было забавное купанье! Мы не могли утонуть. Здесь можно вытянуться на воде во всю длину, лежа на спине и сложив руки на груди, причем большая часть тела будет оставаться над водой. При этом можно совсем поднять голову… Вы можете лежать очень удобно на спине, подняв колени к подбородку и охватив их руками, — но вскоре перевернетесь, так как голова перевешивает. Вы можете встать на голову — и от середины груди до конца ног будете оставаться вне воды, но вы не сможете долго сохранять такое положение. Вы не можете плыть на спине, подвигаясь сколько-нибудь заметно, так как ноги ваши торчат из воды и вам приходится отталкиваться только пятками. Если же вы плывете лицом вниз, то подвигаетесь не вперед, а назад. Лошадь так неустойчива, что не может ни плавать, ни стоять в Мертвом море, — она тотчас же ложится на бок»

На рис. 49 вы видите человека, довольно удобно расположившегося на поверхности Мертвого моря; большой удельный вес воды позволяет ему в этой позе читать книгу, защищаясь зонтиком от жгучих лучей солнца.

Такими же необычайными свойствами обладает вода Кара-Богаз-Гола (залива Каспийского моря[32]) и не менее соленая вода озера Эльтон, содержащая 27% солей.

Нечто в этом роде приходится испытывать тем больным, которые принимают соленые ванны. Если соленость воды очень велика, как, например, в Старорусских минеральных водах, то больному приходится прилагать немало усилий, чтобы удержаться на дне ванны. Я слышал, как женщина, лечившаяся в Старой Руссе, с возмущением жаловалась, что вода «положительно выталкивала ее из ванны». Кажется, она склонна была винить в этом не закон Архимеда, а администрацию курорта…

Рисунок 49. Человек на поверхности Мертвого моря (с фотографии).

Рисунок 50. Грузовая марка на борту корабля. Обозначения марок делаются на уровне ватерлинии. Для отчетливости они показаны также отдельно в увеличенном виде. Значение букв объяснено в тексте.

Степень солености воды в различных морях несколько колеблется, — и соответственно этому суда сидят не одинаково глубоко в морской воде. Быть может, некоторым из читателей случалось видеть на борту судна близ ватерлинии так называемую «Ллойдовскую марку» — знак, показывающий уровень предельных ватерлиний в воде различной плотности. Например, изображенная на рис. 50 грузовая марка означает уровень предельной ватерлинии:

в пресной воде (Fresch Water) — FW

в Индийском океане (India Summer) — IS

в соленой воде летом (Summer) — S

в соленой воде зимой (Winter) — W

в Сев. Атлант. океане зимой (Winter North Atlantik) — WNA

У нас эти марки введены как обязательные с 1909 г. Заметим в заключение, что существует разновидность воды, которая и в чистом виде, без всяких примесей, заметно тяжелее обыкновенной; ее удельный вес 1,1, т. е. на 10% больше, чем обыкновенной; следовательно, в бассейне с такой водой человек, даже не умеющий плавать, едва ли мог бы утонуть. Такую воду назвали «тяжелой» водой; ее химическая формула D₂O (входящий в ее состав водород состоит из атомов, вдвое тяжелее атомов обыкновенного водорода, и обозначается буквой D). «Тяжелая» вода в незначительном количестве растворена в обыкновенной: в ведре питьевой воды ее содержится около 8 г.

Тяжелая вода состава D₂O (разновидностей тяжелой воды различного состава возможно семнадцать) в настоящее время добывается уже почти в чистом виде; примесь обыкновенной воды составляет около 0,05%[33].

Принимая ванну, не упустите случая проделать следующий опыт. Прежде чем покинуть ванну, откройте ее выпускное отверстие, продолжая лежать на ее дне. По мере того как станет выступать над водою все большая и большая часть вашего тела, вы будете ощущать постепенное его отяжеление. Самым наглядным образом убедитесь вы при этом, что вес, утрачиваемый телом в воде (вспомните, как легко чувствовали вы себя в ванне!), появляется вновь, лишь только тело оказывается вне воды.

Когда такой опыт невольно проделывает кит, очутившись во время отлива на мели, последствия оказываются для животного роковыми: его раздавит собственным чудовищным весом. Недаром киты живут в водной стихии: выталкивающая сила жидкости спасает их от гибельного действия силы тяжести.

Сказанное имеет ближайшее отношение к заголовку настоящей статьи. Работа ледокола основана на том же физическом явлении: вынесенная из воды часть корабля перестает уравновешиваться выталкивающим действием воды и приобретает свой «сухопутный» вес. Не следует думать, что ледокол разрезает лед на ходу непрерывным давлением своей носовой части — напором форштевня. Так работают не ледоколы, а ледорезы. Этот способ действия пригоден только для льда сравнительно незначительной толщины.

Подлинные морские ледоколы — такие, как «Красин» или «Ермак», — работают иначе. Действием своих мощных машин ледокол надвигает на поверхность льда свою носовую часть, которая с этой целью устраивается сильно скошенной под водой. Оказавшись вне воды, нос корабля приобретает полный свой вес, и этот огромный груз (у «Ермака» этот вес доходил, например, до 800 тонн) обламывает лед. Для усиления действия в носовые цистерны ледокола нередко накачивают еще воду — «жидкий балласт».

Так действует ледокол до тех пор, пока толщина льда не превышает полуметра. Более мощный лед побеждается ударным действием судна. Ледокол отступает назад и налетает всей своей массой на кромку льда. При этом действует уже не вес, а кинетическая энергия движущегося корабля; судно превращается словно в артиллерийский снаряд небольшой скорости, зато огромной массы, в таран.

Ледяные торосы в несколько метров высоты разбиваются энергией многократных ударов прочной носовой части ледокола.

Участник знаменитого перехода «Сибирякова» в 1932 г., моряк-полярник Н.Марков, так описывает работу этого ледокола:

«Среди сотен ледяных скал, среди сплошного покрова льда „Сибиряков“ начал битву. Пятьдесят два часа подряд стрелка машинного телеграфа прыгала от „полного назад“ к „полному вперед“. Тринадцать четырехчасовых морских вахт „Сибиряков“ с разгона врезался в лед, крошил его носом, влезал на лед, ломал его и снова отходил назад. Лед, толщиной в три четверти метра, с трудом уступал дорогу. С каждым ударом пробивались на треть корпуса».

Самыми крупными и мощными в мире ледоколами располагает СССР.

Распространено мнение, — даже среди моряков, — будто суда, затонувшие в океане, не достигают морского дна, а висят недвижно на некоторой глубине, где вода «соответственно уплотнена давлением вышележащих слоев».

Мнение это разделял, по-видимому, даже автор «20 тысяч лье под водой»; в одной из глав этого романа Жюль Верн описывает неподвижно висящее в воде затонувшее судно, а в другой упоминает о кораблях, «догнивающих, свободно вися в воде».

Правильно ли подобное утверждение?

Некоторое основание для него, как будто, имеется, так как давление воды в глубинах океана действительно достигает огромных степеней. На глубине 10 м вода давит с силой 1 кг на 1 см² погруженного тела. На глубине 20 м это давление равно уже 2 кг, на глубине 100 м — 10 кг, 1000 м — 100 кг. Океан же во многих местах имеет глубину в несколько километров, достигая в самых глубоких частях Великого океана более 11 км (Марианская впадина). Легко вычислить, какое огромное давление должны испытывать вода и погруженные в нее предметы на этих огромных глубинах.

Если порожнюю закупоренную бутылку опустить на значительную глубину и затем извлечь вновь, то обнаружится, что давление воды вогнало пробку внутрь бутылки и вся посудина полна воды. Знаменитый океанограф Джон Меррей в своей книге «Океан» рассказывает, что был проделан такой опыт: три стеклянные трубки различных размеров, с обоих концов запаянные, были завернуты в холст и помещены в медный цилиндр с отверстиями для свободного пропуска воды. Цилиндр был спущен на глубину 5 км. Когда его извлекли оттуда, оказалось, что холст наполнен снегообразной массой: это было раздробленное стекло. Куски дерева, опущенные на подобную глубину, после извлечения тонули в воде, как кирпич, — настолько они были сдавлены.

Естественно, казалось бы, ожидать, что столь чудовищное давление должно настолько уплотнить воду на больших глубинах, что даже тяжелые предметы не будут в ней тонуть, как не тонет железная гиря в ртути.

Однако подобное мнение совершенно не обосновано. Опыт показывает, что вода, как и все вообще жидкости, мало поддается сжатию. Сдавливаемая с силой 1 кг на 1 см² вода сжимается всего только на 1/22 000 долю своего объема и примерно так же сжимается при дальнейшем возрастании давления на каждый килограмм. Если бы мы пожелали довести воду до такой плотности, чтобы в ней плавало железо, необходимо было бы уплотнить ее в 8 раз. Между тем для уплотнения только вдвое, т. е. для сокращения объема наполовину, необходимо давление в 11 000 кг на 1 см² (если бы только упомянутая мера сжатия имела место для таких огромных давлений). Это соответствует глубине 110 км под уровнем океана!

Отсюда ясно, что говорить о сколько-нибудь заметном уплотнении воды в глубине океанов совершенно не приходится. В самом глубоком их месте вода уплотнена лишь на 1100/22000, т. е. на 1/20 нормальной своей плотности, всего на 5%[34]. Это почти не может повлиять на условия плавания в ней различных тел, — тем более, что твердые предметы, погруженные в такую воду, также подвергаются этому давлению и, следовательно, тоже уплотняются.

Не может быть поэтому ни малейшего сомнения в том, что затонувшие суда покоятся на дне океана. «Все, что тонет в стакане воды, — говорит Меррей, — должно пойти ко дну и в самом глубоком океане».

Мне приходилось слышать против этого такое возражение. Если осторожно погрузить стакан вверх дном в воду, он может остаться в этом положении, так как будет вытеснять объем воды, весящий столько же, сколько стакан. Более тяжелый металлический стакан может удержаться в подобном положении и ниже уровня воды, не опускаясь на дно. Точно так же, будто бы, может остановиться на полпути и опрокинутый вверх килем крейсер или другое судно. Если в некоторых помещениях судна воздух окажется плотно запертым, то судно погрузится на определенную глубину и там остановится.

Не мало ведь судов идет ко дну в перевернутом состоянии — и возможно, что некоторые из них так и не достигают дна, оставаясь висеть в темных глубинах океана. Достаточно было бы легкого толчка, чтобы вывести такое судно из равновесия, перевернуть, наполнить водою и заставить упасть на дно, — но откуда взяться толчкам в глубине океана, где вечно царит тишина и спокойствие и куда не проникают даже отголоски бурь?

Все эти доводы основаны на физической ошибке. Перевернутый стакан не погружается в воду сам — его надо внешней силой погрузить в воду, как кусок дерева или пустую закупоренную бутылку. Точно так же и опрокинутый килем вверх корабль вовсе и не начнет тонуть, а останется на поверхности воды. Очутиться на полпути между уровнем океана и его дном он никак не может.

Реальные подводные лодки нашего времени в некоторых отношениях не только догнали фантастический «Наутилус» Жюля Верна, но даже превзошли его. Правда, скорость хода нынешних подводных крейсеров вдвое меньше быстроты «Наутилуса»: 24 узла против 50 у Жюля Верна (узел — около 1,8 км в час). Самый длинный переход современного подводного корабля — кругосветное путешествие, между тем как капитан Немо совершил поход вдвое длиннее. Зато «Наутилус» обладал водоизмещением только в 1500 тонн, имел на борту команду всего из двух-трех десятков человек и способен был оставаться под водой без перерыва не более сорока восьми часов. Подводный крейсер «Сюркуф», построенный в 1929 г. и принадлежавший французскому флоту, имел 3200 тонн водоизмещения, управлялся командой из ста пятидесяти человек и способен был держаться под водой, не всплывая, до ста двадцати часов[35].

Переход от портов Франции до острова Мадагаскара этот подводный крейсер мог совершать, не заходя по пути ни в один порт. По комфортабельности жилых помещений «Сюркуф», быть может, не уступал «Наутилусу». Далее, «Сюркуф» имел перед кораблем капитана Немо и то несомненное преимущество, что на верхней палубе крейсера устроен был водонепроницаемый ангар для разведывательного гидросамолета. Отметим также, что Жюль Верн не снабдил «Наутилус» перископом, дающим лодке возможность обозревать горизонт из-под воды.

В одном лишь отношении реальные подводные корабли долго еще будут далеко отставать от создания фантазии французского романиста: в глубине погружения. Однако приходится отметить, что в этом пункте фантазия Жюля Верна перешла границы правдоподобия. «Капитан Немо, — читаем в одном месте романа, — достигал глубины в три, четыре, пять, семь, девять и десять тысяч метров под поверхностью океана». А однажды «Наутилус» опустился даже на небывалую глубину — в 16 тысяч метров! «Я чувствовал, — рассказывает герой романа, — как содрогаются скрепы железной обшивки подводного судна, как изгибаются его распоры, как подаются внутрь окна, уступая давлению воды. Если бы корабль наш не обладал прочностью сплошного литого тела, его мгновенно сплющило бы в лепешку».

Опасение вполне уместное, потому что на глубине 16 км (если бы такая глубина имелась в океане) давление воды должно было бы достигать 16 000:10 = 1600 кг на 1 см², или 1600 технических атмосфер; такое усилие не раздробляет железа, но безусловно смяло бы конструкцию. Однако подобной глубины современная океанография не знает. Преувеличенные представления о глубинах океана, господствовавшие в эпоху Жюля Верна (роман написан в 1869 г.), объясняются несовершенством способов измерения глубины. В те времена для линь-лота употреблялась не проволока, а пеньковая веревка; такой лот задерживался трением о воду тем сильнее, чем глубже он погружался; на значительной глубине трение возрастало до того, что лот вовсе переставал опускаться, сколько ни травили линь: пеньковая веревка лишь спутывалась, создавая впечатление огромной глубины.

Подводные корабли нашего времени способны выдерживать давление не более 25 атмосфер; это определяет наибольшую глубину их погружения: 250 м. Гораздо большей глубины удалось достигнуть в особом аппарате, названном «батисферой» (рис. 51) и предназначенном специально для изучения фауны океанских пучин. Этот аппарат напоминает, однако, не «Наутилус» Жюля Верна, а фантастическое создание другого романиста — глубоководный шар Уэллса, описанный в рассказе «В морской глубине». Герой этого рассказа спустился до дна океана на глубину 9 км в толстостенном стальном шаре; аппарат погружался без троса, но со съемным грузом; достигнув дна океана, шар освободился здесь от увлекавшего его груза и стремительно взлетел на поверхность воды.

В батисфере ученые достигли глубины более 900 м. Батисфера спускается на тросе с судна, с которым сидящие в шаре поддерживают телефонную связь[36].

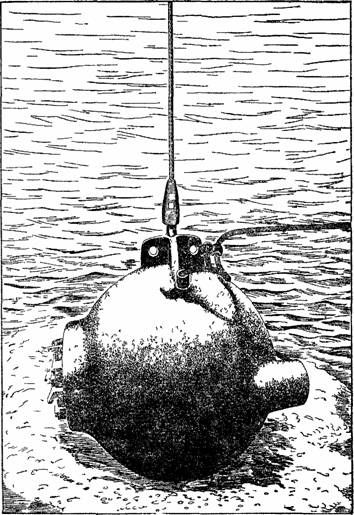Рисунок 51. Стальной шарообразный аппарат «батисфера» для спуска в глубокие слои океана. В этом аппарате Вильям Бийб достиг в 1934 г. глубины 923 м. Толщина стенок шара — около 4 см, диаметр 1,5 м, вес 2,5 тонны.

В широком просторе океана гибнут ежегодно тысячи крупных и мелких судов, особенно в военное время. Наиболее ценные и доступные из затонувших кораблей стали извлекать со дна моря. Советские инженеры и водолазы, входящие в состав ЭПРОН (т. е. «Экспедиции подводных работ особого назначения»), прославились на весь мир успешным подъемом более чем 150 крупных судов. Среди них одно из самых больших — ледокол «Садко», затонувший на Белом море в 1916 г. из-за халатности капитана. Пролежав на морском дне 17 лет, этот превосходный ледокол был поднят работниками ЭПРОН и вступил опять в строй.

Техника подъема была всецело основана на применении закона Архимеда. Под корпусом затонувшего судна в грунте морского дна водолазы прорыли 12 туннелей и протянули сквозь каждый из них прочное стальное полотенце. Концы полотенец были прикреплены к понтонам, намеренно потопленным подле ледокола. Вся эта работа выполнена была на глубине 25 м под уровнем моря.

Понтонами (рис. 52) служили полые непроницаемые железные цилиндры 11 м длиной и 5,5 м в диаметре. Порожний понтон весил 50 тонн. По правилам геометрии легко вычислить его объем: около 250 кубометров. Ясно, что такой цилиндр порожняком должен плавать на воде: он вытесняет 250 тонн воды, сам же весит только 50; грузоподъемность его равна разности между 250 и 50, т. е. 200 тонн. Чтобы заставить понтон опуститься на дно, его заполняют водой.

Когда (см. рис. 52) концы стальных строп были прочно прикреплены к потопленным понтонам, в цилиндры стали с помощью шлангов нагнетать сжатый воздух. На глубине 25 м вода давит с силой 25/10 + 1, т. е. 3,5 атмосферы. Воздух же подавался в цилиндры под давлением около 4 атмосфер и, следовательно, должен был вытеснять воду из понтонов. Облегченные цилиндры с огромной силою выталкивались окружающей водою на поверхность моря. Они всплывали в воде, как аэростат в воздухе. Совместная подъемная их сила при полном вытеснении из них воды равнялась бы 200 × 12, т. е. 2400 тонн. Это превышает вес затонувшего «Садко», так что ради более плавного подъема понтоны были освобождены от воды только частично.

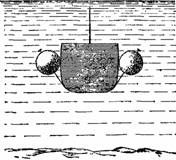Рисунок 52. Схема подъема «Садко»; показан разрез ледокола, понтоны и стропы.

Тем не менее подъем осуществлен был лишь после нескольких неудачных попыток. «Четыре аварии терпела на нем спасательная партия, пока добилась успеха, — пишет руководивший работами главный корабельный инженер ЭПРОН Т. И. Бобрицкий[37]. — Три раза, напряженно ожидая судна, мы видели вместо поднимающегося ледокола стихийно вырывающиеся наверх, в хаосе волн и пены, понтоны и разорванные, змеями извивающиеся шланги. Два раза показывался и снова исчезал в пучине моря ледокол, прежде чем всплыл и окончательно удержался на поверхности».

Среди множества проектов «вечного двигателя» было немало и таких, которые основаны на всплывании тел в воде. Высокая башня в 20 м высоты наполнена водой. Наверху и внизу башни установлены шкивы, через которые перекинут прочный канат в виде бесконечного ремня. К канату прикреплено 14 полых кубических ящиков в метр высоты, склепанных из железных листов так, что внутрь ящиков вода проникнуть не может. Наши рис. 53 и 54 изображают внешний вид такой башни и ее продольный разрез.

Как же действует эта установка? Каждый, знакомый с законом Архимеда, сообразит, что ящики, находясь в воде, будут стремиться всплыть вверх. Их увлекает вверх сила, равная весу воды, вытесняемой ящиками, т. е. весу одного кубического метра воды, повторенному столько раз, сколько ящиков погружено в воду. Из рисунков видно, что в воде оказывается всегда шесть ящиков. Значит, сила, увлекающая погруженные ящики вверх, равна весу 6 м³ воды, т. е. 6 тоннам. Вниз же их тянет собственный вес ящиков, который, однако, уравновешивается грузом из шести ящиков, свободно свисающих на наружной стороне каната.

Итак, канат, перекинутый указанным образом, будет всегда подвержен тяге в 6 тонн, приложенной к одной его стороне и направленной вверх. Ясно, что сила эта заставит канат безостановочно вращаться, скользя по шкивам, и при каждом обороте совершать работу в 6000 × 20 = 120 000 кгм.

Теперь понятно, что если усеять страну такими башнями, то мы сможем получать от них безграничное количество работы, достаточное для покрытия всех нужд народного хозяйства. Башни будут вращать якоря динамомашин и давать электрическую энергию в любом количестве.

Однако если разобраться внимательно в этом проекте, то легко убедиться, что ожидаемого движения каната происходить вовсе не должно.

Чтобы бесконечный канат вращался, ящики должны входить в водяной бассейн башни снизу и покидать его сверху. Но ведь, вступая в бассейн, ящик должен преодолеть давление столба воды в 20 м высотой! Это давление на квадратный метр площади ящика равно ни много, ни мало двадцати тоннам (весу 20 м³ воды). Тяга же вверх составляет всего только 6 тонн, т. е. явно недостаточна, чтобы втащить ящик в бассейн.

Среди многочисленных образчиков водяных «вечных» двигателей, сотни которых придуманы были изобретателями-неудачниками, можно найти очень простые и остроумные варианты.

Рисунок 53. Проект мнимого «вечного» водяного двигателя.

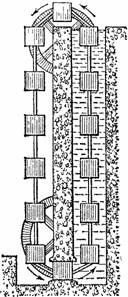Рисунок 54. Устройство башни предыдущего рисунка.

Взгляните на рис. 55. Часть деревянного барабана, укрепленного на оси, все время погружена в воду. Если справедлив закон Архимеда, то погруженная в воду часть должна всплывать и, коль скоро выталкивающая сила больше силы трения на оси барабана, вращение никогда не прекратится…

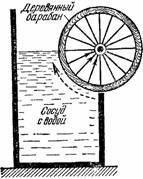Рисунок 55. Еще один проект «вечного» водяного двигателя.

Не спешите с постройкой этого «вечного» двигателя! Вас непременно постигнет неудача: барабан не сдвинется с места. В чем же дело, в чем ошибка наших рассуждений? Оказывается, мы не учли направления действующих сил. А направлены они будут всегда по перпендикуляру к поверхности барабана, т. е. по радиусу к оси. Из повседневного опыта каждый знает, что невозможно заставить колесо вращаться, прикладывая усилия вдоль радиуса колеса. Чтобы вызвать вращение, надо приложить усилие перпендикулярно к радиусу, т. е. по касательной к окружности колеса. Теперь уже нетрудно понять, почему и в этом случае закончится неудачей попытка осуществить «вечное» движение.

Закон Архимеда давал соблазнительную пищу уму искателей «вечного» двигателя и побуждал придумывать хитроумные приспособления для использования кажущейся потери веса в целях получения вечного источника механической энергии.

Слово «газ» принадлежит к числу слов, придуманных учеными наряду с такими словами, как «термометр», «электричество», «гальванометр», «телефон» и прежде всего «атмосфера». Из всех придуманных слов «газ» — безусловно самое короткое. Старинный голландский химик и врач Гельмонт, живший с 1577 по 1644 г. (современник Галилея), произвел «газ» от греческого слова «хаос». Открыв, что воздух состоит из двух частей, из которых одна поддерживает горение и сгорает, остальная же часть не обладает этими свойствами, Гельмонт писал:

«Такой пар я назвал газ, потому что он почти не отличается от хаоса древних» (первоначальный смысл слова «хаос» — сияющее пространство).

Однако новое словечко долго после этого не употреблялось и было возрождено лишь знаменитым Лавуазье в 1789 г. Оно получило широкое распространение, когда всюду заговорили о полетах братьев Монгольфье на первых воздушных шарах.

Ломоносов в своих сочинениях употреблял другое наименование для газообразных тел — «упругие жидкости» (остававшееся в употреблении еще и тогда, когда я учился в школе). Заметим, кстати, что Ломоносову принадлежит заслуга введения в русскую речь ряда названий, ставших теперь стандартными словами научного языка:

атмосфера

манометр

барометр

микрометр

воздушный насос

оптика, оптический

вязкость

э (е) лектрический

кристаллизация

э (е) фир

материя

и др.

Гениальный родоначальник русского естествознания писал по этому поводу: «Принужден я был искать слов для наименования некоторых физических инструментов, действий и натуральных вещей, которые (т. е. слова) хотя сперва покажутся несколько странны, однако надеюсь, что они со временем через употребление знакомее будут».

Как мы знаем, надежды Ломоносова вполне оправдались.

Напротив, предложенные впоследствии В. И. Далем (известным составителем «Толкового словаря») слова для замены «атмосферы» — неуклюжие «мироколица» или «колоземица» — совершенно не привились, как не привился его «небозём» вместо горизонта и другие новые слова.

Самовар, вмещающий 30 стаканов, полон воды. Вы подставляете стакан под его кран и с часами в руках следите по секундной стрелке, во сколько времени стакан наполняется до краев. Допустим, что в полминуты. Теперь зададим вопрос: во сколько времени опорожнится весь самовар, если оставить кран открытым?

Казалось бы, здесь детски-простая арифметическая задача: один стакан вытекает в 0,5 минуты, — значит, 30 стаканов выльются в 15 минут.

Но сделайте опыт. Окажется, что самовар опоражнивается не в четверть часа, как вы ожидали, а в полчаса.

В чем же дело? Ведь расчет так прост!

Прост, но неверен. Нельзя думать, что скорость истечения с начала до конца остается одна и та же. Когда первый стакан вытек из самовара, струя течет уже под меньшим давлением, так как уровень воды в самоваре понизился; понятно, что второй стакан наполнится в больший срок, чем в полминуты; третий вытечет еще ленивее, и т. д.

Скорость истечения всякой жидкости из отверстия в открытом сосуде находится в прямой зависимости от высоты столба жидкости, стоящего над отверстием. Гениальный Торичелли, ученик Галилея, первый указал на эту зависимость и выразил ее простой формулой:

где v — скорость истечения, g — ускорение силы тяжести, a h — высота уровня жидкости над отверстием. Из этой формулы следует, что скорость вытекающей струи совершенно не зависит от плотности жидкости: легкий спирт и тяжеловесная ртуть при одинаковом уровне вытекают из отверстия одинаково быстро (рис. 56). Из формулы видно, что на Луне, где сила тяжести в 6 раз меньше, чем на Земле, потребовалось бы для наполнения стакана примерно в 2,5 раза больше времени, нежели на Земле.

Но возвратимся к нашей задаче. Если после истечения из самовара 20 стаканов уровень воды в нем (считая от отверстия крана) понизился в четыре раза, то 21-й стакан наполнится вдвое медленнее, чем 1-й. И если в дальнейшем уровень воды понизится в 9 раз, то для наполнения последних стаканов понадобится уже втрое больше времени, чем для наполнения первого. Все знают, как вяло вытекает вода из крана самовара, который уже почти опорожнен. Решая эту задачу приемами высшей математики, можно доказать, что время, нужное на полное опорожнение сосуда, в два раза больше срока, в течение которого вылился бы такой же объем жидкости при неизменном первоначальном уровне.

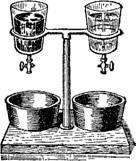Рисунок 56. Что скорее выльется: ртуть или спирт? Уровень жидкости в сосудах одинаков.

От сказанного один шаг к пресловутым задачам о бассейне, без которых не обходится ни один арифметический и алгебраический задачник. Всем памятны классически-скучные, схоластические задачи вроде следующей:

«В бассейн проведены две трубы. Через одну первую пустой бассейн может наполниться в 5 часов; через одну вторую полный бассейн может опорожниться в 10 часов. Во сколько часов наполнится пустой бассейн, если открыть обе трубы сразу?»

Задачи этого рода имеют почтенную давность — без малого 20 веков, восходя к Герону Александрийскому. Вот одна из героновых задач, — не столь, правда, замысловатая, как ее потомки:

Две тысячи лет решаются задачи о бассейнах и — такова сила рутины! — две тысячи лет решаются неправильно. Почему неправильно — вы поймете сами после того, что сейчас сказано было о вытекании воды. Как учат решать задачи о бассейнах? Первую, например, задачу решают так. В 1 час первая труба наливает 0,2 бассейна, вторая выливает 0,1 бассейна; значит, при действии обоих труб в бассейн ежечасно поступает 0,2 – 0,1 = 0,1 откуда для времени наполнения бассейна получается 10 часов. Это рассуждение неверно: если втекание воды можно считать происходящим под постоянным давлением и, следовательно, равномерным, то ее вытекание происходит при изменяющемся уровне и, значит, неравномерно. Из того, что второй трубой бассейн опоражнивается в 10 часов, вовсе не следует, что ежечасно вытекает 0,1 доля бассейна; школьный прием решения, как видим, ошибочен. Решить задачу правильно средствами элементарной математики нельзя, а потому задачам о бассейне (с вытекающей водой) вовсе не место в арифметических задачниках[38].

Рисунок 57. Задача о бассейне.

Возможно ли устроить такой сосуд, из которого вода вытекала бы все время равномерной струёй, не замедляя своего течения, несмотря на то, что уровень жидкости понижается? После того, что вы узнали из предыдущих статей, вы, вероятно, готовы счесть подобную задачу неразрешимой.

Между тем это вполне осуществимо. Банка, изображенная на рис. 58, — именно такой удивительный сосуд. Это обыкновенная банка с узким горлом, через пробку которой вдвинута стеклянная трубка. Если вы откроете кран C ниже конца трубки, то жидкость будет литься из него неослабевающей струёй до тех пор, пока уровень воды не опустится в сосуде до нижнего конца трубки. Вдвинув трубку почти до уровня крана, вы можете заставить всю жидкость, находящуюся выше уровня отверстия, вытечь равномерной, хотя и очень слабой струёй.

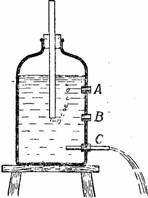Рисунок 58. Устройство сосуда Мариотта. Из отверстия C вода течет равномерно.

Отчего это происходит? Проследите мысленно за тем, что совершается в сосуде при открытии крана C (рис. 58). Прежде всего выливается вода из стеклянной трубки; уровень жидкости внутри нее опускается до конца трубки. При дальнейшем вытекании опускается уже уровень воды в сосуде и через стеклянную трубку входит наружный воздух; он просачивается пузырьками через воду и собирается над ней в верхней части сосуда. Теперь на всем уровне B давление равно атмосферному. Значит, вода из крана C вытекает лишь под давлением слоя воды BC, потому что давление атмосферы изнутри и снаружи сосуда уравновешивается. А так как толщина слоя BC остается постоянной, то и неудивительно, что струя все время течет с одинаковой скоростью.

Попробуйте же теперь ответить на вопрос: как быстро будет вытекать вода, если вынуть пробочку B на уровне конца трубки?

Оказывается, что она вовсе не будет вытекать (разумеется, если отверстие настолько мало, что шириной его можно пренебречь; иначе вода будет вытекать под давлением тонкого слоя воды, толщиной в ширину отверстия). В самом деле, здесь изнутри и снаружи давление равно атмосферному, и ничто не побуждает воду вытекать.

А если бы вы вынули пробку A выше нижнего конца трубки, то не только вода не вытекала бы из сосуда, но в него еще входил бы наружный воздух. Почему? По весьма простой причине: внутри этой части сосуда давление воздуха меньше, чем атмосферное давление снаружи.

Этот сосуд со столь необычайными свойствами был придуман знаменитым физиком Мариоттом и назван по имени ученого «сосудом Мариотта».

В середине XVII столетия жители города Рогенсбурга и съехавшиеся туда владетельные князья Германии во главе с императором были свидетелями поразительного зрелища: 16 лошадей изо всех сил старались разнять два приложенных друг к другу медных полушария. Что связывало их? «Ничто», — воздух. И тем не менее восемь лошадей, тянувших в одну сторону, и восемь, тянувших в другую, оказались не в силах их разъединить. Так бургомистр Отто фон Герике воочию показал всем, что воздух — вовсе не «ничто», что он имеет вес и давит со значительной силой на все земные предметы.

Опыт этот был произведен 8 мая 1654 г. при весьма торжественной обстановке. Ученый бургомистр сумел всех заинтересовать своими научными изысканиями, несмотря на то, что дело происходило в разгар политических неурядиц и опустошительных войн.

Описание знаменитого опыта с «магдебургскими полушариями» имеется в учебниках физики. Все же, я уверен, читатель с интересом выслушает этот рассказ из уст самого Герике, этого «германского Галилея», как иногда называют замечательного физика. Объемистая книга с описанием длинного ряда его опытов вышла на латинском языке в Амстердаме в 1672 г. и, подобно всем книгам этой эпохи, носила пространное заглавие. Вот оно:

ОТТО фон ГЕРИКЕ

первоначально описанные профессором математики

в Вюрцбургском университете КАСПАРОМ ШОТТОМ.

Издание самого автора,

более обстоятельное и пополненное различными

новыми опытами.

Интересующему нас опыту посвящена глава XXIII этой книги. Приводим дословный ее перевод.

«Опыт, доказывающий, что давление воздуха соединяет два полушария так прочно, что их нельзя разнять усилиями 16 лошадей.

Я заказал два медных полушария диаметром в три четверти магдебургских локтя[39]. Но в действительности диаметр их заключал всего 67/100, так как мастера, по обыкновению, не могли изготовить в точности то, что требовалось. Оба полушария вполне отвечали одно другому. К одному полушарию был приделан кран; с помощью этого крана можно удалить воздух изнутри и препятствовать проникновению воздуха снаружи. Кроме того, к полушариям прикреплены были 4 кольца, через которые продевались канаты, привязанные к упряжи лошадей. Я велел также сшить кожаное кольцо; оно напитано было смесью воска в скипидаре; зажатое между полушариями, оно не пропускало в них воздуха. В кран вставлена была трубка воздушного насоса, и был удален воздух внутри шара. Тогда обнаружилось, с какою силою оба полушария придавливались друг к другу через кожаное кольцо. Давление наружного воздуха прижимало их так крепко, что 16 лошадей (рывком) совсем не могли их разнять или достигали этого лишь с трудом. Когда же полушария, уступая напряжению всей силы лошадей, разъединялись, то раздавался грохот, как от выстрела.

Но стоило поворотом крана открыть свободный доступ воздуху — и полушария легко было разнять руками».

Несложное вычисление может объяснить нам, почему нужна такая значительная сила (8 лошадей с каждой стороны), чтобы разъединить части пустого шара. Воздух давит с силою около 1 кг на каждый кв.см; площадь круга[40] диаметром в 0,67 локтя (37 см) равна 1060 см². Значит, давление атмосферы на каждое полушарие должно превышать 1000 кг (1 тонну). Каждая восьмерка лошадей должна была, следовательно, тянуть с силой тонны, чтобы противодействовать давлению наружного воздуха.

Казалось бы, для восьми лошадей (с каждой стороны) это не очень большой груз. Не забывайте, однако, что, двигая, например, кладь в 1 тонну, лошади преодолевают силу не в 1 тонну, а гораздо меньшую, именно — трение колес об оси и о мостовую. А эта сила составляет — на шоссе, например, — всего процентов пять, т. е. при однотонном грузе — 50 кг. (Не говорим уже о том, что при соединении усилий восьми лошадей теряется, как показывает практика, 50% тяги.) Следовательно, тяга в 1 тонну соответствует при восьми лошадях нагрузке телеги в 20 тонн. Вот какова та воздушная поклажа, везти которую должны были лошади магдебургского бургомистра! Они словно должны были сдвинуть с места небольшой паровоз, не поставленный, к тому же, на рельсы.

Измерено, что сильная ломовая лошадь тянет воз с усилием всего в 80 кг[41]. Следовательно, для разрыва магдебургских полушарий понадобилось бы при равномерной тяге 1000/80 = по 13 лошадей с каждой стороны[42].

Читатель будет, вероятно, изумлен, узнав, что некоторые сочленения нашего скелета не распадаются по той же причине, что и магдебургские полушария. Наше тазобедренное сочленение представляет собой именно такие магдебургские полушария. Можно обнажить это сочленение от мускульных и хрящевых связей, и все-таки бедро не выпадает: его прижимает атмосферное давление, так как в межсуставном пространстве воздуха нет.

Обычная форма фонтана, приписываемого древнему механику Герону, вероятно, известна моим читателям, Напомню здесь его устройство, прежде чем перейти к описанию новейших видоизменений этого любопытного прибора. Геронов фонтан (рис. 60) состоит из трех сосудов: верхнего открытого a и двух шарообразных b и c, герметически замкнутых. Сосуды соединены тремя трубками, расположение которых показано на рисунке. Когда в a есть немного воды, шар b наполнен водой, а шар c — воздухом, фонтан начинает действовать: вода переливается по трубке из a в c, вытесняя оттуда воздух в шар b; под давлением поступающего воздуха вода из b устремляется по трубке вверх и бьет фонтаном над сосудом a. Когда же шар b опорожнится, фонтан перестает бить.

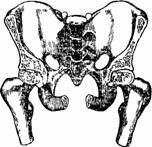Рисунок 59. Кости наших тазобедренных сочленений не распадаются благодаря атмосферному давлению, подобно тому как сдерживаются магдебургские полушария.

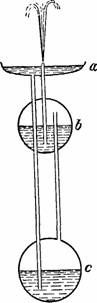Рисунок 60. Старинный геронов фонтан.

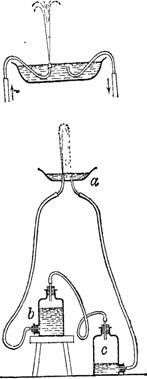Рисунок 61. Современное видоизменение геронова фонтана. Вверху — вариант устройства тарелки.

Такова старинная форма геронова фонтана. Уже в наше время один школьный учитель в Италии, побуждаемый к изобретательности скудной обстановкой своего физического кабинета, упростил устройство геронова фонтана и придумал такие видоизменения его, которые каждый может устроить при помощи простейших средств (рис. 61). Вместо шаров он употребил аптечные склянки; вместо стеклянных или металлических трубок взял резиновые. Верхний сосуд не надо продырявливать: можно просто ввести в него концы трубок, как показано на рис. 61 вверху.

В таком видоизменении прибор гораздо удобнее к употреблению: когда вся вода из банки b перельется через сосуд a в банку c, можно просто переставить банки b и c, и фонтан вновь действует; не надо забывать, разумеется, пересадить также наконечник на другую трубку.

Другое удобство видоизмененного фонтана состоит в том, что он дает возможность произвольно изменять расположение сосудов и изучать, как влияет расстояние уровней сосудов на высоту струи.

Если желаете во много раз увеличить высоту струи, вы можете достигнуть этого, заменив в нижних склянках описанного прибора воду ртутью, а воздух — водой (рис. 62). Действие прибора понятно: ртуть, переливаясь из банки c в банку b, вытесняет из нее воду, заставляя ее бить фонтаном. Зная, что ртуть в 13,5 раза тяжелее воды, мы можем вычислить, на какую высоту должна подниматься при этом струя фонтана. Обозначим разницу уровней соответственно через h1, h2, h3. Теперь разберемся, под действием каких сил ртуть из сосуда c (рис. 62) перетекает в b. Ртуть в соединительной трубке подвержена давлению с двух сторон. Справа на нее действует давление разности h2 ртутных столбов (которое равносильно давлению в 13,5 раза более высокого водяного столба, 13,5 h2) плюс давление водяного столба h1. Слева напирает водяной столб h3. В итоге ртуть увлекается силой

13,5 h2 + h1 – h3.

Но h3 – h1 = h2; заменяем поэтому h1 – h3 на минус h2 и получаем:

13,5 h2 – h2 т. е. 12,5 h2.

Итак, ртуть поступает в сосуд b под давлением веса водяного столба высотой 12,5 h2. Теоретически фонтан должен бить поэтому на высоту, равную разности ртутных уровней в склянках, умноженной на 12,5. Трение несколько понижает эту теоретическую высоту.

Тем не менее описанный прибор дает удобную возможность получить бьющую высоко вверх струю. Чтобы заставить, например, фонтан бить на высоту 10 м, достаточно поднять одну банку над другой примерно на один метр. Любопытно, что, как видно из нашего расчета, возвышение тарелки а над склянками с ртутью нисколько не влияет на высоту струи.

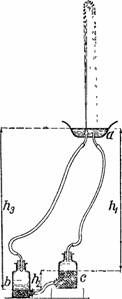Рисунок 62. Фонтан, действующий давлением ртути. Струя бьет раз в десять выше разности уровней ртути.

В старину — в XVII и XVIII веках — вельможи забавлялись следующей поучительной игрушкой: изготовляли кружку (или кувшин), в верхней части которой имелись крупные узорчатые вырезы (рис. 63). Такую кружку, налитую вином, предлагали незнатному гостю, над которым можно было безнаказанно посмеяться. Как пить из нее? Наклонить — нельзя: вино польется из множества сквозных отверстий, а до рта не достигнет ни капли. Случится, как в сказке:

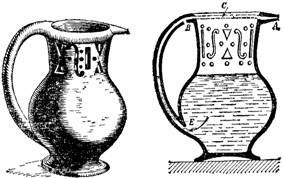Рисунок 63. Обманчивый кувшин конца XVIII века и секрет его устройства.

Но кто знал секрет устройства подобных кружек, — секрет, который показан на рис. 63 справа, — тот затыкал пальцем отверстие B, брал в рот носик и втягивал в себя жидкость, не наклоняя сосуда: вино поднималось через отверстие E по каналу внутри ручки, далее по его продолжению C внутри верхнего края кружки и достигало носика.

Не так давно еще подобные кружки изготовлялись нашими гончарами. Мне случилось в одном доме видеть образчик их работы, довольно искусно скрывающей секрет устройства сосуда; на кружке была надпись: «Пей, но не облейся».

— Ничего, конечно, не весит: в таком стакане вода не держится, выливается, — скажете вы.

— А если не выливается? — спрошу я. — Что тогда?

В самом деле, возможно ведь удержать воду в опрокинутом стакане так, чтобы она не выливалась. Этот случай изображен на рис. 64. Опрокинутый стеклянный бокал, подвязанный за донышко к одной чашке весов, наполнен водой, которая не выливается, так как края бокала погружены в сосуд с водой. На другую чашку весов положен точно такой же пустой бокал.

Какая чашка весов перетянет?

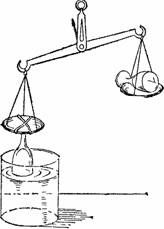Рисунок 64. Какая чашка перетянет?

Перетянет та, к которой привязан опрокинутый бокал с водой. Этот бокал испытывает сверху полное атмосферное давление, снизу же — атмосферное давление, ослабленное весом содержащейся в бокале воды. Для равновесия чашек необходимо было бы наполнить водою бокал, помещенный на другую чашку.

При указанных условиях, следовательно, вода в опрокинутом стакане весит столько же, сколько и в поставленном на дно.

Осенью 1912 г. с океанским пароходом «Олимпик» — тогда одним из величайших в мире судов — произошел следующий случай. «Олимпик» плыл в открытом море, а почти параллельно ему, на расстоянии сотни метров, проходил с большой скоростью другой корабль, гораздо меньший, броненосный крейсер «Гаук». Когда оба судна заняли положение, изображенное на рис. 65, произошло нечто неожиданное: меньшее судно стремительно свернуло с пути, словно повинуясь какой-то невидимой силе, повернулось носом к большому пароходу и, не слушаясь руля, двинулось почти прямо на него. Произошло столкновение. «Гаук» врезался носом в бок «Олимпика»; удар был так силен, что «Гаук» проделал в борту «Олимпика» большую пробоину.

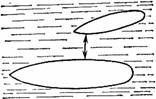Рисунок 65. Положение пароходов «Олимпик» и «Гаук» перед столкновением.

Когда этот странный случай рассматривался в морском суде, виновной стороной был признан капитан гиганта «Олимпик», так как, — гласило постановление суда, — он не отдал никаких распоряжений уступить дорогу идущему наперерез «Гауку».

Суд не усмотрел здесь, следовательно, ничего необычайного: простая нераспорядительность капитана, не больше. А между тем, имело место совершенно непредвиденное обстоятельство: случай взаимного притяжения судов на море.

Такие случаи не раз происходили, вероятно, и раньше при параллельном движении двух кораблей. Но пока не строили очень крупных судов, явление это не проявлялось с такой силой. Когда воды океанов стали бороздить «плавучие города», явление притяжения судов сделалось гораздо заметнее; с ним считаются командиры военных судов при маневрировании.

Многочисленные аварии мелких судов, проплывавших в соседстве с большими пассажирскими и военными судами, происходили, вероятно, по той же причине.

Чем же объясняется это притяжение? Конечно, здесь не может быть и речи о притяжении по закону всемирного тяготения Ньютона; мы уже видели (в гл. IV), что это притяжение слишком ничтожно. Причина явления совершенно иного рода и объясняется законами течения жидкостей в трубках и каналах. Можно доказать, что если жидкость протекает по каналу, имеющему сужения и расширения, то в узких частях канала она течет быстрее и давит на стенки канала слабее, нежели в широких местах, где она протекает спокойнее и давит на стенки сильнее (так называемый «принцип Бернулли»).

То же справедливо и для газов. Это явление в учении о газах носит название эффекта Клеман — Дезорма (по имени открывших его физиков) и нередко именуется «аэростатическим парадоксом». Впервые явление это, как говорят, обнаружено было случайно при следующих обстоятельствах. В одном из французских рудников рабочему приказано было закрыть щитом отверстие наружной штольни, через которую подавался в шахту сжатый воздух. Рабочий долго боролся со струёй воздуха, но внезапно щит сам собой захлопнул штольню с такой силой, что, будь щит недостаточно велик, его втянуло бы в вентиляционный люк вместе с перепуганным рабочим.

Между прочим, этой особенностью течения газов объясняется действие пульверизатора. Когда мы дуем (рис. 67) в колено a, заканчивающееся сужением, то воздух, переходя в сужение, уменьшает свое давление. Таким образом, над трубкой b оказывается воздух с уменьшенным давлением, и потому давление атмосферы гонит жидкость из стакана вверх по трубке; у отверстия жидкость попадает в струю выдуваемого воздуха и в нем распыляется.

Теперь мы поймем, в чем кроется причина притяжения судов. Когда два парохода плывут параллельно один другому, между их бортами получается как бы водяной канал. В обыкновенном канале стенки неподвижны, а движется вода; здесь же наоборот: неподвижна вода, а движутся стенки. Но действие сил от этого нисколько не меняется: в узких местах подвижного канала вода слабее давит на стенки, нежели в пространстве вокруг пароходов. Другими словами, бока пароходов, обращенные друг к другу, испытывают со стороны воды меньшее давление, нежели наружные части судов. Что же должно произойти вследствие этого? Суда должны под напором наружной воды двинуться друг к другу, и естественно, что меньшее судно перемещается заметнее, между тем как более массивное остается почти неподвижным. Вот почему притяжение проявляется с особенной силой, когда большой корабль быстро проходит мимо маленького.

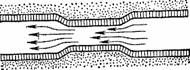Рисунок 66. В узких частях канала вода течет быстрее и давит на стенки слабее, чем в широких.

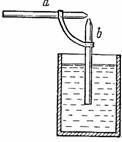Рисунок 67. Пульверизатор.

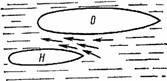Рисунок 68. Течение воды между двумя плывущими судами.

Итак, притяжение кораблей обусловлено всасывающим действием текущей воды. Этим же объясняется и опасность быстрин для купающихся, всасывающее действие водоворотов. Можно вычислить, что течение воды в реке при умеренной скорости 1 м в секунду втягивает человеческое тело с силой 30 кг! Против такой силы не легко устоять, особенно в воде, когда собственный вес нашего тела не помогает нам сохранять устойчивость. Наконец, втягивающее действие быстро несущегося поезда объясняется тем же принципом Бернулли: поезд при скорости 50 км в час увлекает близстоящего человека с силой около 8 кг.

Явления, связанные с «принципом Бернулли», хотя и весьма нередки, мало известны в кругу неспециалистов. Полезно будет поэтому остановиться на нем подробнее. Далее мы приводим отрывок из статьи на эту тему, помещенной в одном научно-популярном журнале.

Принцип, впервые высказанный Даниилом Бернулли в 1726 г., гласит: в струе воды или воздуха давление велико, если скорость мала, и давление мало, если скорость велика. Существуют известные ограничения этого принципа, но здесь мы не будем на них останавливаться.

Рис. 69 иллюстрирует этот принцип.

Воздух продувается через трубку AB. Если сечение трубки мало, — как в a, — скорость воздуха велика; там же, где сечение велико, — как в b, — скорость воздуха мала. Там, где скорость велика, давление мало, а где скорость мала, давление велико. Вследствие малой величины давления воздуха в a жидкость в трубке C поднимается; в то же время сильное давление воздуха в b заставляет опускаться жидкость в трубке D.

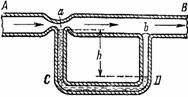Рисунок 69. Иллюстрация принципа Бернулли. В суженной части (a) трубки AB давление меньше, нежели в широкой (b).

На рис. 70 трубка T укреплена на медном диске DD; воздух продувается через трубку T и далее мимо свободного диска dd[43]. Воздух между двумя дисками имеет большую скорость, но эта скорость быстро убывает по мере приближения к краям дисков, так как сечение воздушного потока быстро возрастает и преодолевается инерция воздуха, вытекающего из пространства между дисками. Но давление окружающего диск воздуха велико, так как скорость мала, а давление воздуха между дисками мало, так как скорость велика. Поэтому воздух, окружающий диск, оказывает большее воздействие на диски, стремясь их сблизить, нежели воздушный поток между дисками, стремящийся их раздвинуть; в результате диск dd присасывается к диску DD тем сильнее, чем сильнее ток воздуха в T.

Рис. 71 представляет аналогию рис. 70, но только с водой. Быстро движущаяся вода на диске DD находится на низком уровне и сама поднимается до более высокого уровня спокойной воды в бассейне, когда огибает края диска. Поэтому спокойная вода под диском имеет более высокое давление, чем движущаяся вода над диском, вследствие чего диск поднимается. Стержень P не допускает боковых смещений диска.

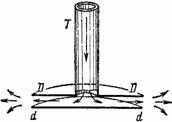Рисунок 70. Опыт с дисками.

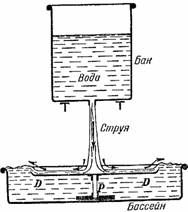Рисунок 71. Диск DD приподнимается на стержне P, когда на него изливается струя воды из бака.

Рис. 72 изображает легкий шарик, плавающий в струе воздуха. Воздушная струя ударяется о шарик и не дает ему падать. Когда шарик выскакивает из струи, окружающий воздух возвращает его обратно в струю, так как давление окружающего воздуха, имеющего малую скорость, велико, а давление воздуха в струе, имеющего большую скорость, мало.

Рис. 73 представляет два судна, движущиеся рядом в спокойной воде, или, что сводится к тому же, два судна, стоящие рядом и обтекаемые водою. Поток более стеснен в пространстве между судами, и скорость воды в этом пространстве больше, чем по обе стороны судов. Поэтому давление воды между судами меньше, чем по обе стороны судов; более высокое давление воды, окружающей суда, сближает их. Моряки очень хорошо знают, что два корабля, идущих рядом, сильно притягиваются друг к другу.

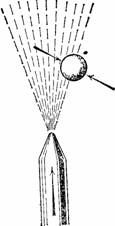Рисунок 72. Шарик, поддерживаемый струей воздуха.

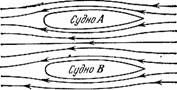Рисунок 73. Два судна, движущиеся параллельно, как бы притягивают друг друга.

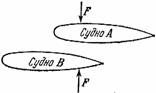Рисунок 74. При движении судов вперед судно B поворачивается носом к судну A.

Рисунок 75. Если между двумя легкими шариками продувать воздух, они сближаются до соприкосновения.

Более серьезный случай может иметь место, когда один корабль идет за другим, как представлено на рис. 74. Две силы F и F, которые сближают корабли, стремятся повернуть их, причем судно B поворачивается к A со значительной силой. Столкновение в таком случае почти неизбежно, так как руль не успевает изменить направление движения корабля.

Явление, описанное в связи с рис. 73, можно демонстрировать, продувая воздух между двумя легкими резиновыми мячиками, подвешенными, как указано на рис. 75. Если между ними продувать воздух, они сближаются и ударяются друг о друга.

О том, какую роль выполняет плавательный пузырь рыб, обыкновенно говорят и пишут — казалось бы, вполне правдоподобно — следующее. Для того чтобы всплыть из глубины в поверхностные слои воды, рыба раздувает свой плавательный пузырь; тогда объем ее тела увеличивается, вес вытесняемой воды становится больше ее собственного веса — и, по закону плавания, рыба поднимается вверх. Чтобы прекратить подъем или опуститься вниз, она, напротив, сжимает свой плавательный пузырь. Объем тела, а с ним и вес вытесняемой воды уменьшаются, и рыба опускается на дно согласно закону Архимеда.

Такое упрощенное представление о назначении плавательного пузыря рыб восходит ко временам ученых Флорентийской академии (XVII в.) и было высказано профессором Борелли в 1685 г. В течение более чем 200 лет оно принималось без возражений, успело укорениться в школьных учебниках, и только трудами новых исследователей (Моро, Шарбонель) была обнаружена полная несостоятельность этой теории.

Пузырь имеет, несомненно, весьма тесную связь с плаванием рыбы, так как рыбы, у которых пузырь был при опытах искусственно удален, могли держаться в воде, только усиленно работая плавниками, а при прекращении этой работы падали на дно. Какова же истинная его роль? Весьма ограниченная: он лишь помогает рыбе оставаться на определенной глубине, — именно на той, где вес вытесняемой рыбой воды равен весу самой рыбы. Когда же рыба работой плавников опускается ниже этого уровня, тело ее, испытывая большое наружное давление со стороны воды, сжимается, сдавливая пузырь; вес вытесняемого объема воды уменьшается, становится меньше веса рыбы, и рыба неудержимо падает вниз. Чем ниже она опускается, тем сильнее становится давление воды (на 1 атмосферу при опускании на каждые 10 м), тем больше сдавливается тело рыбы и тем стремительнее продолжает оно опускаться.

То же самое, только в обратном направлении, происходит тогда, когда рыба, покинув слой, где она находилась в равновесии, перемещается работой плавников в более высокие слои. Тело ее, освободившись от части наружного давления и по-прежнему распираемое изнутри плавательным пузырем (в котором давление газа находилось до этого момента в равновесии с давлением окружающей воды), увеличивается в объеме и вследствие этого всплывает выше. Чем выше рыба поднимается, тем более раздувается ее тело и тем, следовательно, стремительнее ее дальнейший подъем. Помешать этому, «сжимая пузырь», рыба не в состоянии, так как стенки ее плавательного пузыря лишены мышечных волокон, которые могли бы активно изменять его объем.

Что такое пассивное расширение объема тела действительно совершается у рыб, подтверждается следующим опытом (рис. 76). Уклейка в захлороформированном состоянии помещается в закрытый сосуд с водой, в котором поддерживается усиленное давление, близкое к тому, какое господствует на определенной глубине в естественном водоеме; на поверхности воды рыбка лежит бездеятельно, вверх брюшком. Погруженная немного глубже, она вновь всплывает на поверхность. Помещенная ближе ко дну, она опускается на дно. Но в промежутке между обоими уровнями существует слой воды, в котором рыбка остается в равновесии — не тонет и не всплывает. Все это становится понятным если вспомним сказанное сейчас о пассивном расширении и сжатии плавательного пузыря.

Итак, вопреки распространенному мнению, рыба вовсе не может произвольно раздувать и сжимать свой плавательный пузырь. Изменения его объема происходят пассивно, под действием усиленного или ослабленного наружного давления (согласно закону Бойля — Мариотта). Эти изменения объема для рыбы не только не полезны, а, напротив, приносят ей вред, так как обусловливают либо неудержимое, все ускоряющееся падение на дно, либо столь же неудержимый и ускоряющийся подъем на поверхность. Другими словами, пузырь помогает рыбе в неподвижном положении сохранять равновесие, но равновесие это неустойчивое.

Такова истинная роль плавательного пузыря рыб, — поскольку речь идет о его отношении к плаванию; выполняет ли он также и другие функции в организме рыбы и какие именно, — неизвестно, так что орган этот все же является пока загадочным. И только его гидростатическую роль можно считать в настоящее время вполне выясненной.

Наблюдения рыболовов подтверждают сказанное.

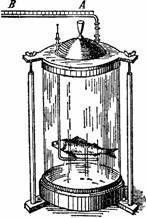Рисунок 76. Опыт с уклейкой.

При ловле рыб из большой глубины случается, что иная рыба на половине пути высвобождается; но, вопреки ожиданию, она не опускается вновь в глубину, из которой была извлечена, а, напротив, стремительно поднимается на поверхность. У таких-то рыб и замечают иногда, что пузырь выпячивается через рот.

Многие из повседневных физических явлений не могут быть объяснены на основе элементарных законов физики. Даже такое часто наблюдаемое явление, как волнение моря в ветреный день, не поддается исчерпывающему объяснению в рамках школьного курса физики. А чем обусловлены волны, разбегающиеся в спокойной воде от носа идущего парохода? Почему волнуются флаги в ветреную погоду? Почему песок на берегу моря располагается волнообразно? Почему клубится дым, выходящий из заводской трубы?

Рисунок 77. Спокойное («ламинарное») течение жидкости в трубе.

Рисунок 78. Вихревое («турбулентное») течение жидкости в трубе.

Чтобы объяснить эти и другие подобные им явления, надо знать особенности так называемого вихревого движения жидкостей и газов. Постараемся рассказать здесь немного о вихревых явлениях и отметить их главные особенности, так как в школьных учебниках о вихрях едва упоминается.

Представим себе жидкость, текущую в трубе. Если все частицы жидкости движутся при этом вдоль трубы по параллельным линиям, то перед нами простейший вид движения жидкости — спокойный, или, как физики говорят, «ламинарный» поток. Однако это вовсе не самый частый случай. Напротив, гораздо чаще жидкости текут в трубах неспокойно; от стенок трубы идут к ее оси вихри. Это — вихреобразное или турбулентное движение. Так течет, например, вода в трубах водопроводной сети (если не иметь в виду тонкие трубы, где течение ламинарное). Вихревое течение наблюдается всякий раз, когда скорость течения данной жидкости в трубе (данного диаметра) достигает определенной величины, так называемой критической скорости[44].

Вихри текущей в трубе жидкости можно сделать заметными для глаз, если в прозрачную жидкость, текущую в стеклянной трубке, ввести немного легкого порошка, например ликоподия. Тогда ясно различаются вихри, идущие от стенок трубки к ее оси.

Эта особенность вихревого течения используется в технике при устройство холодильников и охладителей. Жидкость, текущая турбулентно в трубке с охлаждаемыми стенками, гораздо быстрее приводит все свои частицы в соприкосновение с холодными стенками, нежели при движении без вихрей; надо помнить, что сами по себе жидкости — плохие проводники теплоты и при отсутствии перемешивания охлаждаются или прогреваются очень медленно. Оживленный тепловой и вещественный обмен крови с омываемыми ею тканями также возможен лишь потому, что ее течение в кровеносных сосудах не ламинарное, а вихревое.

Сказанное о трубах относится в равной мере и к открытым каналам и руслам рек: в каналах и реках вода течет турбулентно. При точном измерении скорости течения реки инструмент обнаруживает пульсации, особенно близ дна: пульсации указывают на постоянно меняющееся направление течения, т. е. на вихри. Частицы речной воды движутся не только вдоль речного русла, как обычно представляют себе, но также и от берегов к середине. Оттого и неправильно утверждение, будто в глубине реки вода имеет круглый год одну и ту же температуру, именно +4°C: вследствие перемешивания температура текущей воды близ дна реки (но не озера) такая же, как и на поверхности[45]. Вихри, образующиеся у дна реки, увлекают с собою легкий песок и порождают здесь песчаные «волны». То же можно видеть и на песчаном берегу моря, омываемом набегающей волной (рис. 79). Если бы течение воды близ дна было спокойное, песок на дне имел бы ровную поверхность.

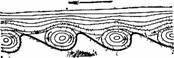Рисунок 79. Образование песчаных волн на морском берегу действием водяных вихрей.

Рисунок 80. Волнообразное движение веревки в текучей воде обусловлено образованием вихрей.

Итак, близ поверхности тела, омываемого водой, образуются вихри. Об их существовании говорит нам, например, змеевидно извивающаяся веревка, протянутая вдоль по течению воды (когда один конец веревки привязан, а другой свободен). Что тут происходит? Участок веревки, близ которого образовался вихрь, увлекается им; но в следующий момент этот участок движется уже другим вихрем в противоположную сторону — получается змеевидное извивание (рис. 80).

От жидкостей перейдем к газам, от воды — к воздуху.

Кто не видал, как воздушные вихри увлекают с земли пыль, солому и т.п? Это — проявление вихревого течения воздуха вдоль поверхности земли. А когда воздух течет вдоль водной поверхности, то в местах образования вихрей, вследствие понижения здесь воздушною давления, вода возвышается горбом — порождается волнение. Та же причина порождает песчаные волны в пустыне и на склонах дюн (рис. 82).

Рисунок 81. Реющий флаг на ветру…

Рисунок 82. Волнообразная поверхность песка в пустыне.

Легко понять теперь, почему волнуется флаг при ветре: с ним происходит то же, что и с веревкой в текучей воде. Твердая пластинка флюгера не сохраняет при ветре постоянного направления, а, повинуясь вихрям, все время колеблется. Такого же вихревого происхождения и клубы дыма, выходящего из заводской трубы; топочные газы протекают через трубу вихревым движением, которое продолжается некоторое время по инерции за пределами трубы (рис. 83).

Велико значение турбулентного движения воздуха для авиации. Крыльям самолета придается такая форма, при которой место разрежения воздуха под крылом оказывается заполненным веществом крыла, а вихревое действие над крылом, напротив, усиливается. В итоге крыло снизу подпирается, а сверху присасывается (рис. 84). Сходные явления имеют место и при парении птицы с распростертыми крыльями.

Рисунок 83. Клубы дыма, выходящего из заводской трубы.

Как действует ветер, обдувающий крышу? Вихри создают над крышей разрежение воздуха; стремясь выровнять давление, воздух из-под крыши, увлекаясь вверх, напирает на нее. В результате происходит то, что, к сожалению, приходится нередко наблюдать: легкая, непрочно прикрепленная крыша уносится ветром. Большие оконные стекла по той же причине при ветре выдавливаются изнутри (а не разламываются напором снаружи). Однако эти явления проще объясняются уменьшением давления в движущемся воздухе (см. выше «Принцип Бернулли», стр. 125).

Когда два потока воздуха разной температуры и влажности текут один вдоль другого, в каждом возникают вихри. Разнообразные формы облаков в значительной мере обусловлены этой причиной.

Мы видим, какой обширный круг явлений связан с вихревыми течениями.

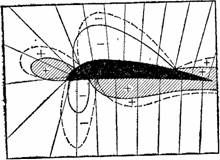Рисунок 84. Каким силам подвержено крыло самолета.

Распределение давлений (+) и разрежений (–) воздуха по крылу на основании опытов. В итоге всех приложенных усилий, подпирающих и засасывающих, крыло увлекается вверх. (Сплошные линии показывают распределение давлений; пунктир — то же при резком увеличении скорости полета)

Ни один человек не опускался еще в Землю глубже 3,3 км, — а между тем радиус земного шара равен 6400 км. До центра Земли остается еще очень длинный путь. Тем не менее изобретательный Жюль Верн спустил глубоко в недра Земли своих героев — чудака-профессора Лиденброка и его племянника Акселя. В романе «Путешествие к центру Земли» он описал удивительные приключения этих подземных путешественников. В числе неожиданностей, встреченных ими под Землей, было, между прочим, и увеличение плотности воздуха. По мере поднятия вверх воздух разрежается очень быстро: его плотность уменьшается в геометрической прогрессии, в то время как высота поднятия растет в прогрессии арифметической. Напротив, при опускании вниз, ниже уровня океана, воздух под давлением вышележащих слоев должен становиться все плотнее. Подземные путешественники, конечно, не могли не заметить этого.

Вот какой разговор происходил между дядей-ученым и его племянником на глубине 12 лье (48 км) в недрах Земли.

«— Посмотри, что показывает манометр? — спросил дядя.

— Очень сильное давление.

— Теперь ты видишь, что, спускаясь помаленьку, мы постепенно привыкаем к сгущенному воздуху и нисколько не страдаем от этого.

— Если не считать боли в ушах.

— Пустяки!

— Хорошо, — отвечал я, решив не противоречить дяде. — Находиться в сгущенном воздухе даже приятно. Вы заметили, как громко раздаются в нем звуки?

— Конечно. В этой атмосфере даже глухой мог бы слышать.

— Но воздух будет становиться все плотнее. Не приобретет ли он в конце концов плотности воды?

— Конечно: под давлением в 770 атмосфер.

— А еще ниже?

— Плотность увеличится еще больше.

— Как же мы станем тогда спускаться?

— Набьем карманы камнями.

— Ну, дядя, у вас на все есть ответ!

Я не стал более вдаваться в область догадок, потому что, пожалуй, опять придумал бы какое-нибудь препятствие, которое рассердило бы дядю. Было, однако, очевидно, что под давлением в несколько тысяч атмосфер воздух может перейти в твердое состояние, а тогда, допуская даже, что мы могли вынести такое давление, придется все же остановиться. Тут уже никакие споры не помогут».

Так повествует романист; но не то окажется, если мы проверим факты, о которых говорится в этом отрывке. Нам не придется спускаться для этого в недра Земли; для маленькой экскурсии в область физики вполне достаточно запастись карандашом и бумагой.

Прежде всего постараемся определить, на какую глубину нужно опуститься, чтобы давление атмосферы возросло на 1000-ю долю. Нормальное давление атмосферы равно весу 760-миллиметрового столба ртути. Если бы мы были погружены не в воздух, а в ртуть, нам надо было бы опуститься всего на 760/1000 = 0,76 мм, чтобы давление увеличилось на 1000-ю долю. В воздухе же, конечно, мы должны опуститься для этого гораздо глубже, и именно во столько раз, во сколько раз воздух легче ртути — в 10 500 раз. Значит, чтобы давление увеличилось на 1000-ю долю нормального, нам придется опуститься не на 0,76 мм, как в ртути, а на 0,76×10500, т. е. почти на 8 м. Когда же мы опустимся еще на 8 м, то увеличенное давление возрастет еще на 1000-то своей величины, и т. д[46]… На каком бы уровне мы ни находились — у самого «потолка мира» (22 км), на вершине горы Эверест (9 км) или близ поверхности океана, — нам нужно опуститься на 8 м, чтобы давление атмосферы возросло на 1000-ю долю первоначальной величины. Получается, следовательно, такая таблица возрастания давления воздуха с глубиной:

На уровне Земли давление

760 мм = нормальному

» глубине 8 м gt;= 1,001 нормального

» глубине 2×8 gt;= (1,001)2

» глубине 3×8 gt;= (1,001)3

» глубине 4×8 gt;= (1,001)4

И вообще на глубине n×8 м давление атмосферы больше нормального в (1,001)n раз; и пока давление не очень велико, во столько же раз увеличится и плотность воздуха (закон Мариотта).

Заметим, что в данном случае речь идет, как видно из романа, об углублении в Землю всего на 48 км, а потому ослабление силы тяжести и связанное с ним уменьшение веса воздуха можно не принимать в расчет.

Теперь можно рассчитать, как велико было, примерно, то давление, которое подземные путешественники Жюля Верна испытывали на глубине 48 км (48 000 м). В нашей формуле n равняется 48000/8 = 6000. Приходятся вычислить 1,001×6000. Так как умножать 1,001 само на себя 6000 раз — занятие довольно скучное и отняло бы много времени, то мы обратимся к помощи логарифмов, о которых справедливо сказал Лаплас, что они, сокращая труд, удваивают жизнь вычислителей[47]. Логарифмируя, имеем: логарифм неизвестного равен

6000 × lg 1,001 = 6000 × 0,00043 = 2,6.

По логарифму 2,6 находим искомое число; оно равно 400.

Итак, на глубине 48 км давление атмосферы в 400 раз сильнее нормального; плотность воздуха под таким давлением возрастет, как показали опыты, в 315 раз. Сомнительно поэтому, чтобы наши подземные путники нисколько не страдали, испытывая только «боль в ушах»… В романе Жюля Верна говорится, однако, о достижении людьми еще больших подземных глубин, именно 120 и даже 325 км. Давление воздуха должно было достигать там чудовищных степеней; человек же способен переносить безвредно для себя воздушное давление не свыше трех-четырех атмосфер.

Если бы по той же формуле мы стали вычислять, на какой глубине воздух становится так же плотен, как и вода, т. е. уплотняется в 770 раз, то получили бы цифру: 53 км. Но этот результат неверен, так как при высоких давлениях плотность газа уже не пропорциональна давлению. Закон Мариотта вполне верен лишь для не слишком значительных давлений, не превышающих сотни атмосфер. Вот данные о плотности воздуха, полученные на опыте:

Давление Плотность

200 атмосфер ... 190

400gt; .............. 315

600gt; .............. 387

1500gt; ............. 513

1800gt; ............. 540

2100gt; ............. 564

Увеличение плотности, как видим, заметно отстает от возрастания давления. Напрасно жюль-верновский ученый ожидал, что он достигнет глубины, где воздух плотнее воды, — этого ему не пришлось бы дождаться, так как воздух достигает плотности воды лишь под давлением 3000 атмосфер, а дальше уже почти не сжимается. О том же, чтобы превратить воздух в твердое состояние одним давлением, без сильнейшего охлаждения (ниже минус 146°), не может быть речи.

Справедливость требует отметить, однако, что упомянутый роман Жюля Верна был опубликован задолго до того, как стали известны приведенные сейчас факты. Это оправдывает автора, хотя и не исправляет повествования.

Воспользуемся еще приведенной раньше формулой, чтобы вычислить наибольшую глубину шахты, на дне которой человек может оставаться без вреда для своего здоровья. Наибольшее воздушное давление, какое еще способен переносить наш организм, — 3 атмосферы. Обозначая искомую глубину шахты через x, имеем уравнение (1,001)x/8 = 3, откуда (логарифмируя) вычисляем x. Получаем x = 8,9 км.

Итак, человек мог бы без вреда находиться на глубине почти 9 км. Если бы Тихий океан вдруг высох, люди могли бы почти повсюду жить на его дне.

Кто ближе всего продвинулся к центру Земли — не в фантазии романиста, а в реальной действительности? Конечно, горнорабочие. Мы уже знаем (см. гл. IV), что глубочайшая шахта мира прорыта в Южной Африке. Она уходит в глубь более чем на 3 км. Здесь имеется в виду не глубина проникновения бурильного долота, достигающая 7,5 км, а углубление самих людей. Вот что рассказывает, например, о шахте на руднике Морро Вельхо (глубина около 2300 м) французский писатель д-р Люк Дюртен, лично посетивший ее:

«Знаменитые золотые прииски Морро Вельхо находятся в 400 км от Рио-де-Жанейро. После 16 часов езды по железной дороге в скалистой местности вы спускаетесь в глубокую долину, окруженную джунглями. Здесь английская компания разрабатывает золотоносные жилы на такой глубине, на какую никогда раньше не спускался человек.

Жила идет в глубь косо. Шахта следует за ней шестью уступами. Вертикальные шахты — колодцы, горизонтальные — туннели. Чрезвычайно характерно для современного общества, что глубочайшая шахта, прорытая в коре земного шара, — самая смелая попытка человека проникнуть в недра планеты — сделана в поисках золота.

Наденьте парусиновую прозодежду и кожаную куртку. Осторожнее: малейший камешек, падающий в колодец, может ранить вас. Нас будет сопровождать один из «капитанов» шахты. Вы входите в первый туннель, хорошо освещенный. Вас охватывает дрожь от леденящего ветра в 4°: это — вентиляция для охлаждения глубин шахты.

Проехав в узкой металлической клетке первый колодец глубиной 700 м, вы попадаете во второй туннель. Спускаетесь во второй колодец; воздух становится теплее. Вы уже находитесь ниже уровня моря.

Начиная со следующего колодца, воздух обжигает лицо. Обливаясь потом, согнувшись под низким сводом, вы подвигаетесь по направлению к реву сверлильных машин. В густой пыли работают обнаженные люди; с них струится пот, руки безостановочно передают бутыль с водой. Не дотрагивайтесь до обломков руды, сейчас отколотых: температура их 57°.

Каков же итог этой ужасной, отвратительной действительности? — Около 10 килограммов золота в день[48]…».

Описывая физические условия на дне шахты и степень крайней эксплуатации рабочих, французский писатель отмечает высокую температуру, но не упоминает о повышенном давлении воздуха. Вычислим, каково оно на глубине 2300 м. Если бы температура оставалась такая же, как на поверхности Земли, то, согласно знакомой уже нам формуле, плотность воздуха возросла бы в

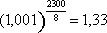раза.

В действительности температура не остается неизменной, а повышается. Поэтому плотность воздуха растет не столь значительно, а меньше. В конечном итоге воздух на дне шахты по плотности разнится от воздуха на поверхности Земли немногим больше, чем воздух знойного летнего дня от морозного воздуха зимы. Понятно теперь, почему это обстоятельство не привлекло к себе внимания посетителя шахты.

Зато большое значение имеет значительная влажность воздуха в таких глубоких рудниках, делающая пребывание в них невыносимым при высокой температуре. В одном из южноафриканских рудников (Иогансбург), глубиною 2553 м, влажность при 50° жары достигает 100%; здесь устраивается теперь так называемый «искусственный климат», причем охлаждающее действие установки равнозначаще 2000 тоннам льда.

В предыдущих статьях мы мысленно путешествовали в земные недра, причем нам помогла формула зависимости давления воздуха от глубины. Отважимся теперь подняться вверх и, пользуясь той же формулой, посмотрим, как меняется давление воздуха на больших высотах. Формула для этого случая принимает такой вид:

p = 0,999h/8,

где p — давление в атмосферах, h — высота в метрах. Дробь 0,999 заменила здесь число 1,001, потому что при перемещении вверх на 8 м давление не возрастает на 0,001, а уменьшается на 0,001.

Решим для начала задачу: как высоко надо подняться, чтобы давление воздуха уменьшилось вдвое?

Для этого приравняем в нашей формуле давление p = 0,5 и станем искать высоту h. Получим уравнение 0,5 = 0,999h/8, решить которое не составит труда для читателей, умеющих обращаться с логарифмами. Ответ h = 5,6 км определяет высоту, на которой давление воздуха должно уменьшиться вдвое.

Направимся теперь еще выше, вслед за отважными советскими воздухоплавателями, достигшими высоты 19 и 22 км. Эти высокие области атмосферы находятся уже в так называемой «стратосфере». Поэтому и шарам, на которых совершаются подобные подъемы, присвоено наименование не аэростатов, а «стратостатов». Не думаю, чтобы среди людей старшего поколения нашелся хотя бы один, который не слыхал бы названий советских стратостатов «СССР» и «ОАХ-1», поставивших в 1933 и 1934 годах мировые рекорды высоты: первый — 19 км, второй — 22 км.

Попытаемся вычислить, каково давление атмосферы на этих высотах.

Для высоты 19 км найдем, что давление воздуха должно составлять

0,999×19000/8 = 0,095 атм = 72 мм.

Для высоты 22 км

0,999×22000/8 = 0,066 атм = 50 мм.

Однако, заглянув в записи стратонавтов, находим, что на указанных высотах отмечены были другие давления: на высоте 19 км — 50 мм, на высоте 22 км — 45 мм.

Почему же расчет не подтверждается? В чем наша ошибка?

Закон Мариотта для газов при столь малом давлении применим вполне, но на этот раз мы сделали другое упущение: считали температуру воздуха одинаковой по всей 20-километровой толще, между тем как она заметно падает с высотой. В среднем принимают, что температура при поднятии на каждый километр падает на 6,5°; так происходит до высоты 11 км, где температура равна минус 56° и далее на значительном протяжении остается неизменной. Если принять это обстоятельство во внимание (для чего уже недостаточны средства элементарной математики), получатся результаты, гораздо более согласные с действительностью. По той же причине на итоги наших прежних вычислений, относящихся к давлению воздуха в глубинах, нужно тоже смотреть как на приближенные.