"Элегантная вселенная (суперструны, скрытые размерности и поиски окончательной теории)" - читать интересную книгу автора (Грин Брайан)

Глава 4. Микроскопические странности

Слегка утомившиеся после своей последней экспедиции за пределы Солнечной системы, Джордж и Грейс вернулись на Землю и решили заглянуть в Н-бар (Игра слов: Н-бар (и оригинале Н-Bar) представляет собой английское чтение символа, которым обозначается постоянная Планка. — Прим. перев.), чтобы немного освежиться после пребывания в космосе. Джордж, как обычно, заказал сок папайи со льдом для себя и водку с тоником для Грейс, откинулся на спинку кресла, скрестил руки за головой и приготовился наслаждаться сигарой, которую он только что зажег. Собравшись затянуться, он вдруг с изумлением обнаружил, что сигара, которая только что была между его зубами, исчезла. Решив, что сигара могла как-нибудь выскользнуть у него изо рта, Джордж наклонился вперед, ожидая увидеть дырку, прожженную на рубашке или на брюках. Но дырки не было. Сигары не было тоже. Грейс, озадаченная странными движениями Джорджа, огляделась вокруг и увидела, что сигара лежит на стойке прямо за стулом Джорджа. «Странно, — сказал Джордж, — как, черт возьми, могла она туда попасть? Такое чувство, что она прошла прямо сквозь мою голову — но язык не обожжен, и я не чувствую в себе никаких новых дырок». Грейс осмотрела Джорджа и неохотно подтвердила, что его язык и голова выглядят совершенно нормально. Поскольку тут как раз подоспели напитки, Джордж и Грейс пожали плечами и отнесли пропавшую сигару к одной из маленьких тайн жизни. Однако чудеса в Н-баре на этом не закончились.

Джордж бросил взгляд на бокал с соком папайи и увидел, что кубики со льдом находятся в непрерывном движении, постоянно сталкиваясь друг с другом и со стенками бокала, как маленькие автомобили в детском аттракционе. На этот раз удивлен был не он один. Грейс держала в руках свой бокал, который был раза в два меньше, чем у Джорджа, и оба они увидели, что ее кубики льда кружились еще более неистово. Они с трудом могли различить отдельные кубики, которые сливались в одну ледяную массу. Но это было ничто по сравнению с тем, что случилось в следующее мгновение. Глядя изумленными глазами на напитки, совершающие стремительную пляску, они вдруг заметили, как один кубик льда прошел сквозь стенку бокала и упал на стойку. Они схватили бокал и увидели, что он совершенно цел; кубик льда каким-то таинственным образом прошел сквозь стекло, не вызвав никаких повреждений. «Должно быть, галлюцинации после прогулок по открытому космосу», — заметил Джордж. Они остановили бешеную пляску ледяных кубиков, осушив одним глотком свои бокалы, и отправились восстанавливаться домой. Торопясь покинуть заведение, Джордж и Грейс даже не заметили, что по ошибке вышли не через обычную дверь, а через декоративную, нарисованную на стене. Однако персонал Н-бара, давно привыкший к людям, проходящим сквозь стены, даже не заметил их поспешного ухода.

Столетие назад, в то время, когда Конрад и Фрейд исследовали потемки человеческой души, немецкий физик Макс Планк впервые пролил свет на квантовую механику — систему понятий, которая провозглашает, помимо всего прочего, что то, с чем столкнулись Джордж и Грейс в Н-баре (если это происходит в микромире), вовсе не требует для своего объяснения привлечения потусторонних сил. Столь необычные и причудливые события типичны для поведения нашей Вселенной, рассматриваемой на сверхмалых масштабах.

Квантовая механика представляет собой систему понятий, предназначенную для понимания свойств микромира. Точно так же, как специальная и общая теории относительности потребовали решительного пересмотра нашего взгляда на мир для случая объектов, которые движутся очень быстро или имеют очень большую массу, квантовая механика установила, что наша Вселенная имеет такие же, если не еше более поразительные свойства, если исследовать ее в масштабе атомных и субатомных расстояний. В 1965 г. Ричард Фейнман, один из величайших специалистов в области квантовой механики, писал: «Было время, когда газеты сообщали, что только двенадцать человек понимают теорию относительности. Я не верю, что такое время когда-либо было. Могло быть время, когда ее понимал только один человек, тот самый парень, который схватил ее суть перед тем, как написать свою статью. Но после того как люди прочитали его статью, масса людей стала так или иначе понимать теорию относительности, и уж точно число этих людей превышало двенадцать. С другой стороны, я думаю, что могу совершенно спокойно сказать, что квантовую механику не понимает никто»1).

Хотя Фейнман высказал свою точку зрения более тридцати лет назад, она остается справедливой и сегодня. Он имел в виду следующее: хотя специальная и общая теории относительности потребовали волнующего пересмотра нашего видения мира, после того, как вы полностью примете лежащие в их основе фундаментальные принципы, все новые и необычные следствия этих теорий для пространства и времени могут быть получены непосредственно путем логических рассуждений. Если вы достаточно интенсивно поработаете над выводами Эйнштейна, приведенными в предыдущих двух главах, вы сможете хотя бы на короткое время понять неизбежность сделанных им заключений. Не так обстоит дело с квантовой механикой. Примерно к 1928 г. уже было установлено множество математических формул и законов квантовой механики. Затем с их помощью неоднократно делались самые точные и успешные в истории науки количественные предсказания. Однако на самом деле те, кто использует квантовую механику, просто следуют формулам и правилам, установленным «отцами-основателями» теории, и четким и недвусмысленным вычислительным процедурам, но без реального понимания того, почему эти процедуры работают, или что они в действительности означают. В отличие от теории относительности едва ли найдется много людей, если такие найдутся вообше, кто смог понять квантовую механику на «интуитивном» уровне.

Что же нам предпринять в такой ситуации? Означает ли это, что в масштабах микромира Вселенная функционирует столь непонятным и непривычным образом, что человеческое мышление, привыкшее в течение тысячелетий иметь дело с явлениями, протекающими в обычном, макроскопическом масштабе, неспособно до конца понять то, «что происходит в действительности»? Или, быть может, по какой-то исторической случайности, физики создали чрезвычайно уродливую формулировку квантовой механики, которая оказалась успешной с точки зрения количественных предсказаний, но маскирует истинную сущность природы? Этого не знает никто. Может быть, когда-нибудь в будущем появится более талантливый исследователь, который предложит новую формулировку, ясно отвечающую на все «почему» и «как» квантовой механики. А может и не появится. Единственное, что мы знаем наверняка, это то, что квантовая механика совершенно ясно и недвусмысленно показывает, что ряд фундаментальных концепций, имеющих существенное значение для понимания того мира, с которым мы сталкиваемся в повседневной жизни, полностью теряет всякий смысл при переходе к микромиру. В результате, пытаясь понять и объяснить Вселенную на атомном и субатомном уровнях, мы должны кардинально менять наш язык и логику рассуждений.

В последующих разделах мы рассмотрим основы этого языка и опишем ряд удивительных результатов, к которым ведет его применение. Если по ходу изложения квантовая механика покажется вам в целом странной и нелепой, вы должны вспомнить о двух ве-щах. Во-первых, помимо того, что это математически корректная теория, единственная причина, по которой мы доверяем квантовой механике, состоит в том, что ее предсказания подтверждаются с поразительной точностью. Если кто-то сможет рассказать вам со всеми мучительными подробностями массу самых сокровенных историй из вашего детства, трудно будет не поверить, что это ваш давно пропавший брат (или сестра). Во-вторых, вы не одиноки в такой реакции на квантовую механику. Сходной точки зрения придерживалось, в большей или меньшей степени, немало уважаемых физиков. Эйнштейн отказывался признать квантовую механику. И даже Нильс Бор, один из первооткрывателей квантовой механики, однажды заметил, что если вы никогда не чувствуете себя ошеломленным, когда размышляете о квантовой механике, значит, вы не понимаете ее по-настоящему.

Путь к квантовой механике начался с одной сбивающей с толку проблемы. Представьте, что стоящая у вас в доме духовка имеет идеальную изоляцию, что вы установили ее на некоторую температуру, скажем, 200° С, и что у вас достаточно времени, чтобы подождать, пока она нагреется. Даже если перед включением духовки вы откачаете из нее весь воздух, она будет излучать волны в результате нагрева стенок. Это тот же вид излучения (теплота и свет являются разновидностями электромагнитных волн), что и излучение поверхности Солнца или раскаленной докрасна железной кочерги.

Проблема состоит в следующем. Электромагнитные волны переносят энергию. Например, жизнь на Земле критически зависит от солнечной энергии, переносимой с Солнца на Землю электромагнитными волнами. В начале XX столетия физики рассчитали общее количество энергии электромагнитного излучения замкнутой полости, находящейся при заданной температуре. Используя хорошо известные методы расчета, они получили нелепый ответ: при любой заданной температуре общая энергия оказывалась бесконечной.

Всем было ясно, что это нонсенс — духовка может дать значительное количество энергии, но уж точно не бесконечное. Для того чтобы понять решение, предложенное Планком, стоит рассмотреть проблему более детально. Оказалось, что когда электромагнитная теория Максвелла применяется для расчета излучения духовки, она показывает, что волны, генерируемые стенками, должны быть такими, чтобы между противоположными стенками укладывалось целое число максимумов и минимумов. Несколько примеров показано на рис. 4.1.

Рис. 4.1. Теория Максвелла говорит нам, что волны излучения в духовке имеют целое число максимумов и минимумов — они совершают полные циклы колебаний

Рис. 4.2. Длина волны определяется как расстояние между соседними максимумами или минимумами. Амплитуда представляет собой наибольшую высоту или глубину волны.

Физики используют для описания таких волн три понятия: длина волны, частота и амплитуда. Длина волны, как показано на рис. 4.2, представляет собой расстояние между соседними максимумами или минимумами волны. Чем больше максимумов и минимумов, тем короче длина волны, так как все они должны уместиться между неподвижными стенками печи. Частота обозначает число циклов колебаний вверх-вниз, которые волна совершает в течение одной секунды. Частота и длина волны являются взаимосвязанными параметрами: чем больше длина волны, тем меньше частота; чем меньше длина волны, тем больше частота. Чтобы понять, почему это так, представьте себе, что вы создаете волны, раскачивая один конец длинного каната, другой конец которого привязан к стенке. Для того чтобы получить волну с большой длиной волны, вы лениво помахиваете концом каната вверх и вниз. Частота волн равна числу движений вашей руки за секунду и, следовательно, является очень небольшой. Чтобы генерировать более короткую волну, вам придется трясти ваш конец более интенсивно, более часто: это даст волну более высокой частоты. Наконец, физики используют термин амплитуда для описания максимальной высоты или глубины волны (см. рис. 4.2).

Если электромагнитные волны вам кажутся слишком абстрактными, есть другая хорошая аналогия: волны, воспроизводимые при игре на струнах скрипки. Разные длины волн соответствуют разным музыкальным нотам: чем выше частота, тем выше нота. Амплитуда волны, создаваемой скрипичной струной, определяется тем, с какой силой вы цепляете смычком по струне. При большей силе вы вкладываете больше энергии в колебания струны; следовательно, большее количество энергии соответствует большей амплитуде. Результатом будет более громкий звук. Аналогично меньшее количество энергии соответствует меньшей амплитуде и меньшей громкости звука.

Используя установленные в XIX в. уравнения термодинамики, физики смогли определить, какое количество энергии передают горячие стенки духовки электромагнитным волнам каждой разрешенной длины волны, т. е. фактически насколько сильно стенки «цепляют» каждую волну. Полученный результат оказался весьма простым: каждая из разрешенных волн независимо от ее длины волны будет нести одно и то же количество энергии (которое определяется температурой духовки). Иными словами, когда речь идет о количестве переносимой энергии, все возможные волны в духовке оказываются в совершенно равноправном положении.

На первый взгляд мы получили интересный и довольно безобидный результат. Однако это совсем не так. Он провозгласил крах того, что называлось классической физикой. Причина состоит в следующем. Даже при ограничении, чтобы все волны имели целое число максимумов и минимумов, — что исключает огромное число видов волн, — в печи по-прежнему остается бесконечное количество волн с нарастающим количеством максимумов и минимумов. Поскольку каждая волна несет одно и то же количество энергии, бесконечное число волн будет переносить бесконечное количество энергии. Так на рубеже столетий в бочке меда теоретической физики объявилась огромная «гаргантюанская» ложка дегтя.

В 1900 г. Планк высказал удивительную догадку, позволившую решить эту головоломку и принесшую ему Нобелевскую премию 1918 г. по физике2). Для того чтобы понять решение Планка, представьте себе, что вы вместе с огромной толпой людей, «бесконечной» по количеству, ютитесь в огромном и холодном ангаре, принадлежащем скаредному домовладельцу. На стенке установлен затейливый цифровой термостат, который регулирует температуру. Узнав, сколько домовладелец требует в уплату за отопление, вы потрясены. Если термостат установлен на 15° С, каждый должен платить домовладельцу по 15 долларов. Если он установлен на 16° С, каждый платит по 16 долларов и т. д. Вы понимаете, что поскольку кроме вас помещение арендует бесконечное число съемщиков, как только отопление будет включено, домовладелец станет получать бесконечную сумму денег.

Однако, более внимательно прочитав правила оплаты, вы обнаруживаете лазейку. Ваш домовладелец очень занятой человек, он не хсчет терять время на отсчитывание сдачи, особенно бесконечному количеству отдельных съемщиков. Поэтому он устанавливает следующую систему оплаты. Те, кто могут выплатить точную сумму без сдачи, платят строго по счету. Остальные платят столько, сколько могут набрать имеющимися у них купюрами, но так, чтобы не нужно было давать сдачи. Поэтому, желая привлечь к оплате всех и, в то же время, избежать непомерной платы за тепло, вы уговариваете своих компаньонов разделить все деньги по следующему принципу. Один из вас собирает все центы, другой — все пятицентовые монеты, третий — все десятицентовые, четвертый — все двадцатипятицентовые и т.д., включая тех, кто будет хранить однодолларовые банкноты, пятидолларовые, десятидолларовые, двадцатидолларовые, пятидесятидолларовые, стодолларовые и даже банкноты более крупных (и незнакомых) номиналов. Вы нахально устанавливаете термостат на 25° С и ждете появления домовладельца. Когда он приходит, тот компаньон, у которого все центы, платит ему первым, отсчитывая 2 500 монеток. Затем хранитель пятицентовых монет отдает 500 монет; хранитель десятицентовых монет отдает 250 монет, далее платит обладатель 100 двадцатипятицентовых монет, затем идет парень с долларами, отдающий домовладельцу 25 бумажек. Далее хранитель пятидолларовых купюр передает 5 банкнот, а хранитель десятидолларовых банкнот ограничивается только 2 банкнотами (поскольку три десятидолларовые банкноты уже превышают сумму, подлежащую уплате, и требуют сдачи). Ваш компаньон с купюрами по 20 долларов также ограничивается только 1 банкнотой (ибо с двух уже потребуется сдача), а у всех остальных номинал имеющихся у них купюр — минимальная порция денег — превышает требуемую к оплате сумму. Поэтому они не могут заплатить домовладельцу, и в результате, вместо того, чтобы получить бесконечную сумму денег, на которую рассчитывал домовладелец, он удаляется с жалкими 190 долларами.

Планк использовал очень похожий подход для того, чтобы обойти абсурдный вывод о бесконечном количестве энергии в духовке и получить конечное значение. Вот как он добился этого. Планк смело предположил, что количество энергии, переносимой электромагнитной волной в духовке, подобно деньгам, изменяется порциями. Энергия может быть равна одному такому фундаментальному «номиналу энергии», или двум, или трем и т. д. — но это все. Согласно Планку, когда речь идет об энергии, доли не допустимы, точно так же, как вы не можете иметь монету в одну треть цента или в половину от двадцати пяти центов. (В настоящее время денежные номиналы США определяются федеральным казначейством.) В поисках более фундаментального объяснения Планк предположил, что энергетический номинал волны, т.е. минимальное количество энергии, которое она может нести, определяется ее частотой. Точнее, он постулировал, что минимальная энергия, которую может нести волна, пропорциональна ее частоте: большая частота (более короткая длина волны) предполагает большую минимальную энергию, меньшая частота (большая длина волны) — меньшую минимальную энергию. Можно привести такое грубое сравнение: так же, как пологие океанские волны длинны и величественны, а сильные коротки и порывисты, длинноволновое излучение менее энергично, чем коротковолновое.

Расчеты Планка показали, что дискретность допустимой энергии волн избавляет от нелепого результата о бесконечной суммарной энергии. Нетрудно понять, почему это так. Когда духовка нагревается до некоторой заданной температуры, то согласно расчетам, основанным на термодинамике XIX в., каждая волна вносит свой вклад в общую энергию. Однако, подобно компаньонам, которые не могут внести обычную сумму платы домовладельцу, поскольку номинал их денег слишком велик, если минимальная энергия, которую может переносить конкретная волна, превышает ее ожидаемый энергетический вклад, она не дает вклада вообще и остается безучастной. Поскольку минимальная энергия, которую может нести волна, согласно Планку, пропорциональна ее частоте, то, исследуя волны в духовке и переходя к волнам со все более высокой частотой (все меньшей длиной волны), рано или поздно обнаружится, что минимальная энергия, которую может нести волна, превышает ожидаемый энергетический вклад. Подобно компаньонам, которым доверили банкноты с номиналом, превышающим двадцать долларов, эти волны с возрастающими частотами не могут дать вклада, которого требует физика XIX в. Аналогично тому, что только конечное число компаньонов смогло заплатить за тепло, и общая сумма оказалась конечной, только конечное число волн может дать вклад в общую энергию печи, что опять же приводит к конечности полного количества энергии. Говорим ли мы об энергии или о деньгах, порционность фундаментальных единиц и все возрастающий размер этих единиц по мере того, как мы переходим к более высоким частотам (или к более крупным купюрам), приводит к замене бесконечного ответа конечным3).

Избавившись от очевидно абсурдного бесконечного результата, Планк сделал важный шаг. Но то, что действительно заставило людей поверить в справедливость его догадки — замечательное совпадение результата его нового подхода для вычисления энергии в духовке с экспериментальными данными. Планк обнаружил, что подстроив один параметр, входящий в его новую расчетную схему, можно точно предсказать результаты измерения энергии в духовке для любой заданной температуры. Этот параметр представляет собой коэффициент пропорциональности между частотой волны и минимальным количеством энергии, которую волна может нести. Планк установил, что этот коэффициент пропорциональности, известный ныне как постоянная Планка и обозначаемый символом, составляет в обычных единицах примерно одну миллиардную от одной миллиардной от одной миллиардной доли4'. Ничтожно малая величина постоянной Планка означает, что размер порций энергии обычно очень мал. По этой причине нам, например, кажется, что мы заставляем энергию волны, создаваемой струной скрипки (и, следовательно, громкость звука), изменяться непрерывно. В действительности, однако, энергия волны изменяется дискретными шагами согласно формуле Планка, но размер этих шагов настолько мал, что дискретные скачки от одного уровня громкости к другому кажутся нам плавными переходами. По утверждению Планка, амплитуда этих скачков энергии растет по мере увеличения частоты волны (сопровождаемого уменьшением длины волны). Это тот основной момент, который разрешает парадокс бесконечной энергии.

Как мы увидим далее, квантовая гипотеза Планка не просто позволяет понять энергетику духовки, но идет гораздо дальше. Она опрокидывает многое из того, что мы считали само собой разумеющимся. Малое значение постоянной Планка заточает в границы микромира большинство отклонений от привычной картины, но если бы постоянная была гораздо больше, то происходящие в Н-баре странные вещи стали бы обыденными. Как мы увидим, аналоги этих странностей являются привычным делом в микромире.

Планк не мог обосновать гипотезу дискретности энергии волн, играющую центральную роль в предложенном им решении. За исключением того, что это работает, ни у Планка, ни у кого-либо еще не было никакого рационального объяснения, почему все должно быть именно так. Как заметил однажды физик Георгий Гамов, это подобно тому, как если бы природа разрешала либо пить целый литр пива, либо не пить совсем, не допуская никаких промежуточных доз5). В 1905 г. Эйнштейн нашел объяснение, за которое он получил Нобелевскую премию 1921 г. по физике.

Эйнштейн пришел к своему объяснению, пытаясь решить проблему, известную под названием фотоэлектронной эмиссии (фотоэффекта). В 1887 г. немецкий физик Генрих Герц впервые обнаружил, что когда электромагнитное излучение (свет) падает на некоторые металлы, они испускают электроны. Само по себе это свойство не слишком удивительно. Известно, что некоторые из электронов металлов слабо связаны с ядрами атомов (именно поэтому металлы являются столь хорошими проводниками электричества). Когда свет сталкивается с поверхностью металла, он отдает энергию: при столкновении с вашей кожей это приводит к нагреву тела. Переданная энергия может возбуждать электроны в металлах, при этом некоторые из слабосвязанных электронов могут выбиваться с поверхности.

Странные свойства фотоэффекта становятся явными при более детальном изучении характеристик испускаемых электронов. На первый взгляд может показаться, что при увеличении интенсивности (яркости) света скорость вылетевших электронов также должна увеличиваться, поскольку падающее электромагнитное излучение будет нести больше энергии.

Однако этого не происходит. Вместо этого происходит увеличение числа вылетевших электронов, но их скорость остается постоянной. С другой стороны, было экспериментально установлено, что скорость вылетевших электронов увеличивается при увеличении частоты падающего света и, соответственно, уменьшается при ее уменьшении. (Для электромагнитных волн в видимой части спектра увеличение частоты соответствует изменению цвета от красного к оранжевому, желтому, зеленому, голубому, синему и, наконец, к фиолетовому. Излучение, частота которого превышает частоту фиолетового света, невидимо: эта часть спектра начинается с ультрафиолетового излучения, за которым следует рентгеновское. Электромагнитные волны, частота которых ниже частоты красного света, также невидимы; они соответствуют инфракрасному излучению.) В действительности, при уменьшении частоты света наступает момент, когда скорость вылетевших электронов падает до нуля, и они перестают вылетать с поверхности независимо от интенсивности источника света. По какой-то неизвестной причине цвет падающего луча света, а не его полная энергия, определяет, испускаются ли электроны, и если испускаются, то какую энергию имеют.

Чтобы понять, как Эйнштейн объяснил эти загадочные факты, вернемся к нашему арендуемому помещению, которое теперь нагревается до комфортной температуры 25° С. Представим, что ненавидящий детей домовладелец потребовал, чтобы все, кому не исполнилось пятнадцати лет, жили в подвале, который взрослые могут видеть с балкона, опоясывающего здание. Более того, любой из огромного количества детей в подвале может выйти из здания, лишь заплатив привратнику плату за выход в 85 центов. (Этот домовладелец такой негодяй.) Взрослые, которые согласно вашему предложению распределили все деньги по номиналам в соответствии с описанной выше схемой, могут передать деньги детям, только бросая их с балкона. Давайте посмотрим, что при этом произойдет.

Держатель одноцентовых монет бросает несколько из них вниз, но это слишком малая сумма, чтобы кто-то из детей мог заплатить за выход. И, поскольку внизу находится «бесконечное» море детей, с криками сражающихся за падающие монеты, то даже если обладатель центов бросит огромное количество монет, ни один ребенок не сможет собрать 85 центов, которые он должен уплатить. То же самое получится у тех взрослых, которые владеют пятицентовыми, десятицентовыми и двадцатипятицентовыми монетами. Хотя каждый из них бросит вниз огромное количество денег, любой ребенок сочтет за счастье, если ему достанется хотя бы одна монета (большинство же не получит ни одной), и уж точно никто не сможет набрать сумму в 85 центов, необходимую для выхода из подвала. Но когда деньги начнет бросать владелец однодолларовых купюр — даже небольшими суммами, доллар за долларом, — те счастливчики, кому удастся поймать одну единственную банкноту, смогут сразу же покинуть подвал. Обратите внимание, что даже когда этот человек наверху как следует расщедрится и начнет бросать доллары бочками, количество выходящих детей увеличится во много раз, но у каждого останется ровно 15 центов после получения сдачи у привратника. Это будет справедливо независимо от числа брошенных долларов.

Рассмотрим теперь, как применить все это к фотоэффекту. Основываясь на рассмотренных выше экспериментальных данных, Эйнштейн решил распространить планковскую дискретную модель энергии волны на новое определение света. Согласно Эйнштейну, световой луч должен рассматриваться как поток микроскопических частиц света, окрещенных химиком Гильбертом Льюисом фотонами (мы уже использовали этот термин в примере со световыми часами, приведенном в главе 2). Для того чтобы дать представление о масштабах в рамках корпускулярной модели света, скажем, что обычная электрическая лампочка мощностью 100 Вт излучает примерно сто миллиардов миллиардов (1020) фотонов в секунду. Эйнштейн использовал это новое положение для объяснения механизма, лежащего в основе фотоэффекта. Он предположил, что электрон вырывается с поверхности металла, если с ним столкнется фотон, обладающий достаточным количеством энергии. А чем определяется энергия отдельного фотона? Для объяснения экспериментальных данных Эйнштейн вслед за Планком предположил, что энергия каждого фотона пропорциональна частоте световой волны (при этом коэффициент пропорциональности равен постоянной Планка).

Тогда, как и в случае минимальной суммы, необходимой для уплаты за выход ребенка, чтобы вырваться с поверхности, электроны в металле должны испытать соударение с фотоном, обладающим определенным минимальным количеством энергии. (Как и в случае с детьми, сражающимися за деньги, вероятность того, что отдельно взятый электрон испытает соударение более чем с одним фотоном исчезающе мала — большинство электронов не испытает вообще ни одного соударения.) Однако если частота падающего света слишком мала, энергия составляющих его фотонов будет недостаточной, чтобы вырывать электроны. Точно так же, как никто из детей не сможет покинуть подвал, несмотря на огромное количество мелких монет, которые им бросят взрослые, ни один электрон не сможет выйти из металла, несмотря на огромное общее количество энергии, содержащейся в падающем свете, если его частота (и, следовательно, энергия отдельных фотонов) будет слишком низкой.

Но так же, как дети смогут начать покидать подвал, как только номинал бросаемых им денег станет достаточно большим, электроны начнут вырываться с поверхности металла, как только частота падающего на них света — его энергетический номинал — станет достаточно высокой. Далее, так же, как в случае, когда владелец однодолларовых купюр увеличил общую сумму сбрасываемых денег, увеличив число бросаемых банкнот, интенсивность луча света, имеющего заданную частоту, возрастет при увеличении числа фотонов, которые он содержит. И точно так же, как большее число долларов приведет к тому, что больше детей смогут покинуть подвал, увеличение числа фотонов приведет к тому, что большее число электронов испытает соударение и покинет металл. Обратите внимание, что энергия каждого из этих электронов после выхода из металла зависит исключительно от частоты светового луча, а не от его суммарной интенсивности. Так же, как дети покидают подвал с 15 центами, независимо от того, сколько купюр было брошено им с балкона, каждый электрон покидает поверхность с одной и той же энергией и, следовательно, с одной и той же скоростью, независимо от общей интенсивности падающего света. Большее количество денег просто означает, что большее число детей смогут покинуть подвал; большая суммарная энергия светового луча означает, что больше электронов будет вырвано из металла. Если мы хотим, чтобы дети покидали подвал с большим количеством денег, мы должны увеличить номинал купюр, которые им бросаем; если мы хотим, чтобы электроны выходили из металла с большей скоростью, следует увеличить частоту падающего светового луча, т. е. увеличить энергетический номинал фотонов, которые падают на поверхность металла.

Сказанное полностью подтверждается экспериментальными данными. Частота света (его цвет) определяет скорость вылетающих электронов, суммарная интенсивность света — количество вылетевших электронов. Таким образом, Эйнштейн показал, что гипотеза Планка о дискретности энергии на самом деле отражает фундаментальное свойство электромагнитных волн: они состоят из частиц — фотонов, которые представляют собой маленькие порции или кванты света. Дискретность энергии, заключенной в таких волнах, связана с тем, что они состоят из дискретных объектов.

Прозрение Эйнштейна представляло собой большой шаг вперед. Но, как мы увидим ниже, история была не такой гладкой, как может показаться.

Каждому известно, что вода (и, следовательно, волны на поверхности воды) состоит из огромного количества молекул. Поэтому так ли удивительно, что световые волны тоже состоят из огромного числа частиц — фотонов? Удивительно. Но главный сюрприз кроется в деталях. Дело в том, что более трехсот лет назад Ньютон провозгласил, что свет представляет собой поток частиц, так что сама идея не нова. Однако ряд коллег Ньютона, среди которых наиболее выделялся голландский физик Христиан Гюйгенс, оспорили это мнение, утверждая, что свет представляет собой волну. Долгое время этот вопрос был предметом ожесточенных дебатов, пока эксперименты, выполненные в начале XIX в. английским физиком Томасом Юнгом, не показали, что Ньютон ошибался.

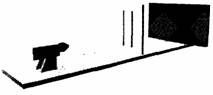
Вариант установки в эксперименте Юнга, известном под названием опыта с двумя щелями, схематически показан на рис. 4.3. Фейнман любил говорить, что вся квантовая механика может быть выведена путем тщательного осмысливания следствий одного этого эксперимента, поэтому он заслуживает того, чтобы рассмотреть его поподробнее. Как видно из рис. 4.3, свет падает на сплошную преграду, в которой сделаны две щели. Свет, который прошел через щели, регистрируется на фотопластинке — более светлые области на фотографии указывают на те места, куда попало больше света. Эксперимент состоит в сравнении картин, полученных на фотопластинках, когда открыты одна или обе щели и включен источник света.

Рис. 4.3. В эксперименте с двумя щелями луч света падает на преграду, в которой проделаны две щели. Когда открыта одна или обе щели, луч света, проходящий через преграду, регистрируется с помощью фотопластинки.

Рис. 4.4. В этом опыте открыта правая щель, в результате изображение на фотопластинке будет выглядеть, как показано на рисунке.

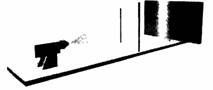
Если левая щель закрыта, а правая открыта, фотография будет выглядеть, как показано на рис. 4.4. Картина вполне объяснима, поскольку свет, который попадает на фотопластинку, проходит только через одну щель и поэтому концентрируется в правой части фотографии. Аналогично, если мы закроем правую щель, а левую оставим открытой, фотография будет выглядеть, как показано на рис. 4.5.

Рис. 4.5. Те же условия, как и в опыте, показанном на рис. 4.4, за исключением того, что открыта левая щель.

Если открыты обе щели, то картина, предсказываемая ньютоновской корпускулярной моделью света, должна выглядеть, как показано на рис. 4.6, представляющем собой комбинацию рис. 4.4 и 4.5.

Рис. 4.6. Ньютоновская корпускулярная модель предсказывает, что когда будут открыты обе щели, картина на фотопластинке будет представлять собой объединение картин, показанных на рис. 4.4 и 4.5.

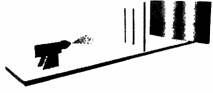По существу, если представить ньютоновские световые корпускулы в виде маленьких дробинок, которыми вы обстреливаете преграду, то те из дробинок, которые пройдут сквозь нее, будут концентрироваться в двух полосах, положение которых соответствует положению щелей. Волновая же модель света, напротив, ведет к совершенно иному предсказанию, если открыты обе щели. Посмотрим, что происходит в этом случае.

Представим, что вместо световых волн мы рассматриваем волны на поверхности воды. Это не повлияет на результат, но такие волны более наглядны. Когда волна сталкивается с преградой, то, как показано на рис. 4.7, от каждой щели распространяется новая волна, похожая на ту, которая возникает, если бросить камешек в пруд. (Это легко проверить, используя картонный лист с двумя прорезями, помещенный в чашку с водой.) Когда волны, идущие от каждой щели, накладываются друг на друга, происходит интересное явление. При наложении двух волновых максимумов высота волны в соответствующей точке увеличивается — она равна сумме высот максимумов двух наложившихся волн. Аналогично, при наложении двух минимумов глубина впадины, образовавшейся в этой точке, также увеличивается. Наконец, если максимум одной волны совпадает с минимумом другой, они взаимно гасят друг друга. (На этом основана конструкция фантастических шумопоглощающих наушников — они определяют форму пришедшей звуковой волны и генерируют другую, форма которой в точности «противоположна» первой, что приводит к подавлению нежелательного шума.) Между этими крайними случаями — максимум с максимумом, минимум с минимумом и максимум с минимумом — расположен весь спектр частичного усиления и частичного ослабления. Если вы с компанией друзей сядете в небольшие лодки, выстроите их в линию параллельно преграде и каждый из вас будет сообщать, насколько сильно его качает при прохождении волны, результат будет похож на тот, который изображен на рис. 4.7.

Рис. 4.7. Круговые волны на воде, идущие от каждой щели, накладываются одна на другую; это приводит к тому, что в одних местах результирующая волна будет усиливаться, а в других ослабляться.

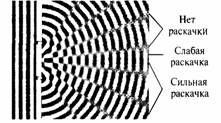Точки с сильной качкой будут расположены там, где накладываются максимумы (или минимумы) волн, приходящих от разных щелей. Участки с минимальной качкой или полным ее отсутствием окажутся там, где максимумы волны, идущей от одной щели, будут совпадать с минимумами волны, идущей от другой щели.

Поскольку фотографическая пластинка регистрирует, насколько сильно она «раскачивается» под влиянием падающего света, из приведенных выше рассуждений, примененных к волновой картине, создаваемой лучом света, следует, что когда открыты обе щели, фотография будет иметь вид, показанный на рис. 4.8. Самые яркие участки на рис. 4.8 представляют области, в которых максимумы (или минимумы) световых волн, пришедших от разных щелей, совпадают. Темными являются участки, в которых максимум одной волны складывается с минимумом другой, приводя к взаимному погашению. Такая последовательность светлых и темных полос известна под названием интерференционной картины.

Рис. 4.8. Если свет представляет собой волну, тс в тех случаях, когда открыты обе щели, будет про исходить интерференция между волнами, прошед шими через разные щели.

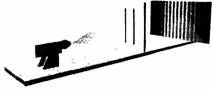Эта фотография существенно отличается от рис. 4.6, и, следовательно, требуется эксперимент, который позволил бы установить, какая из теорий права — корпускулярная или волновая. Подобный эксперимент был выполнен Юнгом, и его результат совпал с картиной, показанной на рис. 4.8, тем самым подтвердив волновую природу света. Ньютоновская теория корпускулярной природы света была отвергнута (хотя потребовалось некоторое время, прежде чем все физики согласились с этим). Доминирующая волновая теория света впоследствии получила надежное математическое обоснование в теории Максвелла.

Но Эйнштейн, низвергнувший заслуженную теорию гравитации Ньютона, похоже, возродил ньютоновскую корпускулярную модель света, введя понятие фотонов. Конечно, перед нами по-прежнему стоит вопрос: как объяснить интерференционную картину, показанную на рис. 4.8, с точки зрения корпускулярной теории? На первый взгляд можно предложить следующее объяснение. Вода состоит из молекул Н2О — «частиц» воды. Однако когда огромные количества этих молекул движутся в одном потоке, они могут создавать волны на поверхности воды, с присущими этим волнам интерференционными свойствами, показанными на рис. 4.7. Можно предположить, что в корпускулярной модели света волновые эффекты, например, интерференционные картины, возникают благодаря взаимодействию огромного числа световых корпускул — фотонов.

В действительности, однако, микромир устроен гораздо более тонко. Даже если интенсивность источника света на рис. 4.8 начнет уменьшаться вплоть до такого значения, когда в сторону преграды один за другим будут излучаться одиночные фотоны со скоростью, скажем, один фотон в десять секунд, результат на фотопластинке будет выглядеть точно так же, как показано на рис. 4.8. Если вы подождете достаточно долго, чтобы огромное число этих отдельных частиц света прошло через щели и оставило свой след в виде точек на фотопластинках, эти точки образуют показанную на рис. 4.8 интерференционную картину. Это поразительно. Как могут отдельные фотоны, последовательно проходящие через экран и независимо сталкивающиеся с фотопластинкой, «сговориться» и воспроизвести яркие и темные полосы интерференционной картины? Здравый смысл говорит нам, что каждый фотон проходит либо через левую, либо через правую щель, и результирующая картина должна быть похожа на ту, которая показана на рис. 4.6. Но это не так.

Если этот факт не поразил вас, это значит, что либо вы уже сталкивались с ним и знаете ему объяснение, либо наше описание является недостаточно наглядным. Если дело в последнем, попробуем взглянуть на это явление еще раз, но под несколько иным углом зрения. Итак, вы закрываете левую щель и пускаете фотоны на преграду, один за другим. Некоторые из них проходят через преграду, некоторые нет. Те, которые прошли, точка за точкой создают изображение на фотопластинке, которое выглядит, как показано на рис. 4.4. Вслед за этим вы проводите эксперимент с новой фотопластинкой, но на этот раз открываете обе щели. Как и следовало ожидать, вы считаете, что это только увеличит число фотонов, прошедших через преграду и попавших на фотографическую пластинку, т. е. на пластинку попадет больше света, чем в первом опыте. Но когда позднее вы изучаете полученную фотографию, вы видите, что наряду с участками, которые были темными в первом опыте и стали светлыми во втором, есть участки, которые были светлыми в первом опыте, а во втором стали темными, как на рис. 4.8. Увеличив число фотонов, попавших на фотопластинку, вы уменьшили яркость некоторых участков. Каким-то образом отдельные фотоны, разделенные во времени, смогли нейтрализовать друг друга. Подумайте о всей неординарности того, что произошло: фотоны, которые прошли через правую щель и попали на пленку в одной из темных полос на рис. 4.8, не смогли сделать этого при открытой левой щели (поэтому пленка и осталась темной). Но как могло повлиять на крошечную частицу света, прошедшую через одну щель, то обстоятельство, была ли открыта другая щель? Фейнман однажды заметил, что это так же странно, как если бы вы стреляли по экрану из пулемета, и когда были открыты обе щели, то отдельные, независимо вылетевшие пули каким-то образом нейтрализовали друг друга, оставляя непораженные участки на экране — участки, которые были поражены, когда открытой была только одна щель.

Эти эксперименты показали, что частицы света Эйнштейна довольно существенно отличаются от частиц Ньютона. Каким-то образом фотоны — хотя они и являются частицами — обладают также и волновыми свойствами света. Тот факт, что энергия этих частиц определяется параметром, используемым для описания волн, т. е. частотой, является первым признаком того, что это странное объединение действительно имеет место. Однако фотоэффект и эксперимент с двумя щелями еще более озадачивают нас. Фотоэффект показывает, что свет имеет свойства частиц. Эксперимент с двумя щелями демонстрирует, что свет также проявляет интерференционные свойства, характерные для волн. Вместе они показывают, что свет обладает и волновыми, и корпускулярными свойствами. Микромир требует, чтобы при попытке его описания мы отказались от наших интуитивных представлений о том, что любой объект представляет собой либо волну, либо частицу, и чтобы мы учитывали возможность того, что он может быть волной и частицей одновременно. Это один из тех случаев, когда высказывание Фейнмана о том, что «никто не понимает квантовую механику», является особенно актуальным. Мы можем произносить слова типа «корпускулярно-волновой дуализм». Мы можем преобразовать эти слова в математическую модель, которая воспроизведет экспериментальные данные с поразительной точностью. Но добиться глубокого, интуитивного понимания этой ошеломляющей особенности микромира необычайно трудно.

В течение первых десятилетий XX в. многие крупнейшие физики-теоретики неустанно трудились над разработкой математически строгой и физически обоснованной теории, объясняющей остававшиеся доселе неведомыми свойства микромира. Так, под руководством Нильса Бора был достигнут значительный прогресс в объяснении свойств света, излучаемого атомами водорода при высокой температуре. Однако эта и другие работы, выполненные до середины 1920-х гг., представляли собой скорее временный союз идей XIX столетия с впервые полученными концепциями квантовой механики, а не гармоничную систему понимания мироздания. По сравнению с ясными и логичными системами ньютоновских законов движения или электромагнитной теории Максвелла, разработанная только частично квантовая механика находилась в хаотическом состоянии.

В 1923 г. молодой французский аристократ, князь Луи де Бройль, добавил новый элемент в квантовую мешанину, который вскоре помог разработать математический аппарат современной квантовой механики и принес ему Нобелевскую премию 1929 г. по физике. Вдохновленный цепочкой рассуждений, восходящих к специальной теории относительности Эйнштейна, де Бройль предположил, что корпускулярно-волновой дуализм применим не только к свету, но и к веществу. Его аргументы, если опустить детали, состоят в том, что эйнштейновское уравнение Е = тс2 связывает массу с энергией; но с другой стороны, Планк и Эйнштейн связали энергию с частотой волн. Объединяя эти два факта, можно прийти к выводу, что масса должна иметь и волновое воплощение. После долгих размышлений де Бройль предположил, что так же, как свет является волновым явлением, которое, как показывает квантовая теория, имеет равно обоснованное корпускулярное описание, так и электрон, который мы обычно считаем частицей, может иметь равно обоснованное волновое описание. Эйнштейн сразу принял идею де Бройля, поскольку она была естественным развитием его собственного вклада в теорию относительности и теорию фотонов. Однако без экспериментального подтверждения все равно нельзя было обойтись. Такое подтверждение было вскоре получено в работах Клинтона Дэвиссона и Лестера Джермера.

В середине 1920-х гг. Дэвиссон и Джермер, физики-экспериментаторы из лаборатории телефонной компании Белл, исследовали рассеяние электронов на атомах никеля. Для нас их исследования интересны тем, что кристаллы никеля в этих экспериментах действовали во многом подобно щелям в опыте, описанном и проиллюстрированном в предыдущем разделе. На самом деле можно считать эксперименты практически идентичными, за исключением того, что вместо луча света использовался пучок электронов. Дэвиссон и Джермер исследовали электроны, пропуская их через две щели, сквозь которые они могли попадать на фосфоресцирующий экран, оставляя на нем светящиеся точки, точно так же, как на экране телевизора, и обнаружили поразительное явление. На экране появлялась картина, очень похожая на ту, которая показана на рис. 4.8. Эксперимент, таким образом, показывал, что электроны создают интерференционную картину, которая является неоспоримым признаком волн. В темных точках на фосфоресцирующем экране электроны каким-то образом «нейтрализовали» друг друга, совсем как при наложении гребней и впадин волн, распространяющихся по поверхности волны. Даже если «сжать» пучок электронов до такой степени, что один электрон будет излучаться один раз в десять секунд, отдельные электроны по-прежнему будут образовывать яркие и темные полосы — по одному пятну за один раз. Как и фотоны, отдельные электроны каким-то образом «интерферируют» сами с собой в том смысле, что с течением времени отдельные электроны воссоздают интерференционную картину, которая ассоциируется с волнами. Мы с неизбежностью вынуждены заключить, что наряду с более привычным описанием на языке частиц каждый электрон проявляет и волновые свойства.

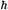Описанные выше эксперименты относятся к электронам, однако схожие эксперименты позволяют сделать вывод о том, что все вещество имеет волновые свойства. Но как это согласуется с нашим повседневным опытом, говорящем о том, что вещество — это нечто сплошное и твердое, и уж никак не похожее на волны? Де Бройль предложил формулу для длины волны частиц вещества, которая показывает, что длина волны пропорциональна постоянной Планка h. (Если говорить более точно, длина волны определяется как частное от деления на импульс материального тела.) Поскольку величина очень мала, длина волны также является очень малой по обычным масштабам. Именно по этой причине волновые характеристики материи становятся наблюдаемыми только в высокоточных микроскопических исследованиях. Точно так же, как большая величина скорости света с скрывает истинные свойства пространства и времени, малость маскирует волновые свойства материи в окружающем нас мире.

Явление интерференции, открытое Дэвиссоном и Джермером, реально продемонстрировало, что электроны подобны волнам. Но при этом возникает естественный вопрос: волнам чего? Одно из первых предположений на эту тему, сделанное австрийским физиком Эрвином Шредингером, заключалось в том, что эти волны представляют собой «размазанные» электроны. Это предположение отчасти улавливало «сущность» электронной волны, но было слишком неточным. Когда вы размазываете что-нибудь, часть его находится здесь, а другая часть в другом месте. Однако никому и никогда не приходилось иметь дело с половиной или с третью, или с иной частью электрона. Это усложняло понимание того, что представляет собой размазанный электрон. В 1926 г. немецкий физик Макс Борн существенно уточнил предложенную Шредингером интерпретацию электронной волны, и именно этой интерпретацией, усиленной Бором и его коллегами, мы пользуемся и сегодня. Утверждение Борна касается одного из самых странных свойств квантовой теории, тем не менее, оно подтверждается огромным количеством экспериментальных данных. Согласно этому утверждению электронная волна должна интерпретироваться с точки зрения вероятности. В тех областях, где амплитуда (или, точнее, квадрат амплитуды) волны больше, обнаружение электрона более вероятно; в местах, где амплитуда мала, вероятность обнаружить электрон меньше. Пример показан на рис. 4.9.

Рис. 4.9. Волна, ассоциированная с электроном, имеет наибольшую амплитуду в тех местах, где обнаружение электрона наиболее вероятно; амплитуда волны убывает по мере уменьшения вероятности обнаружения электрона.

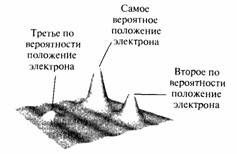Это действительно необычная идея. Какое отношение имеет вероятность к формулировке фундаментальных законов физики? Мы привыкли к тому, что вероятность присуща лошадиным бегам, подбрасыванию монеты или игре в рулетку, но в этих случаях она просто является отражением неполноты нашего знания. Если мы точно знаем скорость колеса рулетки, вес и твердость шарика, который бегает по нему, положение и скорость шарика в тот момент, когда он падает на колесо, свойства материала ячеек и т. п., и если мы используем для наших вычислений достаточно мощные компьютеры, мы можем, в соответствии с законами классической физики, совершенно точно предсказать, где остановится шарик. В казино полагаются на неспособность игрока получить всю эту информацию и провести необходимые вычисления перед тем, как сделать ставку. Однако ясно, что вероятность, с которой приходится сталкиваться во время игры в рулетку, не отражает никаких фундаментальных свойств Вселенной. Напротив, квантовая механика вводит понятие вероятности в устройство мироздания на гораздо более глубоком уровне. Согласно утверждению Борна, подкрепленному собранными более чем за полвека экспериментальными данными, наличие у материи волновых свойств подразумевает, что фундаментальное описание материи должно иметь вероятностный характер. Закон де Бройля показывает, что для макроскопических объектов, таких как кофейная чашка или рулеточное колесо, волновые свойства являются практически ненаблюдаемыми, и в обычных ситуациях связанная с ними квантово-механическая вероятность может полностью игнорироваться. Но этот же закон говорит, что на микроскопическом уровне мы, в лучшем случае, можем указать только вероятность того, что электрон будет обнаружен в любом заданном месте.

Допустим, что электронные волны обладают теми же свойствами, что и все другие волны, например, они могут сталкиваться с препятствиями и образовывать вторичные волны. Однако в рамках вероятностного описания из этого не следует, что сам электрон распадается на части. Это означает лишь, что имеются области, в которых электрон может появиться с ненулевой вероятностью. На практике это означает, что если мы будем снова и снова повторять совершенно одинаковым образом какой-либо эксперимент с электроном, касающийся, например, измерения его положения, мы не будем всегда получать одинаковый результат. Повторяющиеся эксперименты дадут набор различных результатов, в которых частота появления электрона в заданном месте будет функцией плотности вероятности электронной волны. Если функция плотности вероятности для волны (или, точнее, квадрат плотности вероятности) для точки А в два раза больше, чем для точки В, то при многократном повторении опыта мы увидим, что электрон будет обнаруживаться в точке А в два раза чаще, чем в точке В. Точный результат эксперимента не может быть предсказан; лучшее, что можно сделать — предсказать вероятность данного возможного исхода.

Однако если математическое выражение для функции плотности вероятности известно точно, то даже при такой неопределенности исходов вероятностный прогноз может быть проверен путем многократного повторения эксперимента, что позволяет экспериментально определить вероятность того или иного конкретного результата. Всего через несколько месяцев после появления гипотезы де Бройля Шредингер сделал важный шаг в этом направлении, предложив уравнение, которое определяет форму и эволюцию таких вероятностных волн, или, как они теперь называются, волновых функций. Вскоре уравнение Шредингера и вероятностная интерпретация были использованы для получения фантастически точных предсказаний. Таким образом, к 1927 г. классическая наивность была утрачена. Ушли те дни, когда Вселенная представлялась работавшим как часы механизмом, объекты которого, приведенные в движение в какой-то момент в прошлом, покорно следовали к неизбежному, единственным образом определяемому пункту назначения. Согласно квантовой механике Вселенная развивается в соответствии со строгими и точными математическими законами, но эти законы определяют только вероятность того, что может наступить то или иное конкретное будущее, и ничего не говорят о том, какое будущее наступит в действительности.

Многие сочтут этот вывод обескураживающим или даже совершенно неприемлемым. Одним из таких людей был Эйнштейн. В одном из наиболее известных в истории физики высказываний он предостерегал сторонников квантовой механики: «Бог не играет в кости со Вселенной». Он считал, что вероятность появляется в фундаментальной физике по той же причине, по которой она появляется в игре в рулетку: вследствие существенной неполноты нашего знания. С точки зрения Эйнштейна, во Вселенной нет места для будущего, точное содержание которого включает элементы вероятности. Физики должны предсказывать, как будет развиваться Вселенная, а не определять вероятность того, что события могут пойти каким-то путем. Но эксперимент за экспериментом (некоторые из наиболее впечатляющих были выполнены уже после его смерти) убедительно подтверждали, что Эйнштейн был не прав. Как заметил однажды по этому поводу британский физик-теоретик Стивен Хокинг. «Заблуждался Эйнштейн, а не квантовая теория»6).

Тем не менее, споры о том, что же в действительности представляет собой квантовая механика, не утихают. Все согласны в том, как использовать уравнения квантовой механики для получения точных предсказаний. Нет согласия в вопросах о том, что в действительности представляют собой волновые функции, каким образом частица «выбирает», какому из многих вариантов будущего ей следовать. Нет согласия даже в вопросе о том, действительно ли она выбирает или вместо этого разделяется, подобно разветвляющемуся руслу реки, и живет во всех возможных будущих, в вечно расширяющемся мире параллельных вселенных. Эти интерпретации сами по себе заслуживают отдельной книги, и, в действительности, есть немало превосходных книг, пропагандирующих тот или иной взгляд на квантовую теорию. Но совершенно определенным кажется тот факт, что независимо от интерпретации квантовой механики, она неопровержимо доказывает, что Вселенная основана на принципах, которые являются неестественными с точки зрения повседневного опыта.

Общий урок, который дают теория относительности и квантовая механика, состоит в том, что в ходе глубоких исследований основ мироздания можно столкнуться с фактами, которые очень сильно отличаются от наших ожиданий. Отвага при постановке новых вопросов может потребовать непредвиденной гибкости, когда нам придется принимать неожиданные точки зрения.

Ричард Фейнман был одним из величайших физиков-теоретиков со времен Эйнштейна. Он полностью принял вероятностную интерпретацию квантовой механики, но после Второй мировой войны предложил новый взгляд на эту теорию. С позиций численных предсказаний точка зрения Фейнмана полностью согласуется с тем, что было известно ранее. Но ее формулировка существенно отличается от общепринятой. Рассмотрим ее в контексте экспериментов с электронами и двумя щелями.

Проблема с интерпретацией рис. 4.8 возникает потому, что в нашем представлении электрон проходит либо через левую щель, либо через правую, и поэтому мы рассчитываем увидеть комбинацию картин рис. 4.4 и 4.5, показанную на рис. 4.6. Электрону, проходящему через правую щель, должно быть все равно, существует ли левая щель, и наоборот. Но каким-то образом он ее чувствует. Получаемая интерференционная картина требует взаимодействия и сообщения между чем-то, чувствительным к обеим щелям, даже если электроны выстреливаются поодиночке. Шредингер, де Бройль и Борн объясняли этот феномен, приписывая каждому электрону волновую функцию. Подобно волнам на поверхности воды, показанным на рис. 4.7, волны функции плотности вероятности электрона «видят» обе щели и испытывают своего рода интерференцию при наложении. На тех участках, где вероятностная волна усиливается при наложении, подобно участкам значительного усиления колебаний на рис. 4.7, обнаружение электрона вероятно, а там, где вероятностная волна ослабляется при наложении, подобно местам с минимальной амплитудой или отсутствием колебаний на рис. 4.7, обнаружение электрона маловероятно или невероятно. Электроны сталкиваются с фосфоресцирующим экраном один за другим, распределенные в соответствии с функцией плотности вероятности и, в конечном итоге, образуют интерференционную картину, схожую с той, которая показана на рис. 4.8.

Фейнман выбрал другой подход. Он усомнился в основном классическом предположении, согласно которому каждый электрон проходит либо через левую щель, либо через правую. На первый взгляд это предположение настолько фундаментально, что сомневаться в нем нелепо. В конце концов, разве вы не можете заглянуть в область, расположенную между щелями и фосфоресцирующим экраном, и посмотреть, сквозь какую щель проходит каждый электрон? Да, вы можете. Но тем самым вы измените эксперимент. Чтобы увидеть электрон, вы должны сделать с ним что-нибудь — например, осветить его, т. е. столкнуть с ним фотон. В повседневных масштабах фотон действует как исчезающе малый зонд, который отскакивает от деревьев, картин и людей, не оказывая практически никакого влияния на движение этих сравнительно больших материальных тел. Но электрон — это ничтожно малая частица материи. Независимо от того, насколько осторожно вы будете определять щель, через которую он прошел, отражающиеся от электрона фотоны неизбежно повлияют на его последующее движение. А это изменение движения изменит результат нашего эксперимента. Если ваше вмешательство будет достаточно сильным для того, чтобы вы смогли определить щель, через которую прошел электрон, результат эксперимента изменится, и вместо картины, показанной на рис. 4.8, вы получите картину, подобную той, которая изображена на рис. 4.6! Квантовый мир гарантирует, что как только вы установили, через какую щель, правую или левую, прошел каждый электрон, интерференция между этими двумя щелями исчезнет.

Таким образом, Фейнман укрепился в своих сомнениях: хотя повседневный опыт говорит о том, что электрон должен проходить через одну из двух щелей, к концу 1920-х гг. физики поняли, что любая попытка проверить это якобы фундаментальное свойство неизбежно приведет к искажению результатов эксперимента.

Фейнман провозгласил, что каждый электрон, который проходит через преграду и попадает на фосфоресцирующий экран, проходит через обе щели. Это звучит дико, но не торопитесь возмущаться, вас ждут еще более сумасшедшие заявления. Фейнман высказал утверждение, что на отрезке от источника до некоторой точки на фосфоресцирующем экране каждый отдельно взятый электрон на самом деле перемещается по всем возможным траекториям одновременно; некоторые из этих траекторий показаны на рис. 4.10.

Рис. 4.10. Согласно формулировке квантовой механики, предложенной Фейнманом, частица, перемещающаяся из одной точки в другую, движется одновременно по всем возможным путям. Здесь показано несколько из бесконечного числа возможных траекторий для одного электрона, движущегося от источника к фосфоресцирующему экрану. Обратите внимание, что этот один электрон на самом деле проходит через обе щели.

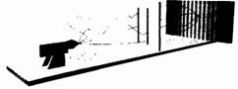Электрон вполне упорядоченным образом проходит через левую щель. Одновременно он столь же упорядоченно проходит через правую щель. Он направляется к левой щели, но вдруг меняет направление и устремляется к правой. Он петляет вперед и назад и, наконец, проходит через левую щель. Он отправляется в долгое путешествие к туманности Андромеды, там он разворачивается, возвращается назад и проходит через левую щель на пути к экрану. Он движется и так и этак — согласно Фейнману, электрон одновременно «рыщет» по всем возможным путям, соединяющим пункт отправления и пункт назначения.

Фейнман показал, что каждому из этих путей можно поставить в соответствие некоторое число, и общее среднее этих чисел даст ту же вероятность, что и расчет с использованием волновой функции. Итак, с точки зрения Фейнмана, с электроном не нужно связывать никакой вероятностной волны. Вместо этого мы должны представить себе нечто столь же, если не более, странное. Вероятность того, что электрон, — который во всех отношениях проявляет себя частицей, — появится в некоторой заданной точке экрана, определяется суммарным эффектом от всех возможных путей, ведущих в эту точку. Этот подход к квантовой механике известен как фейнмановское «суммирование по путям»7).

Здесь начинает протестовать наше классическое образование: как может один электрон одновременно перемещаться по различным путям, да еще и по бесконечному числу путей? Это возражение кажется неоспоримым, но квантовая механика — реальная физика нашего мира — требует, чтобы вы держали столь тривиальные возражения при себе. Результаты расчетов с использованием фейнмановского подхода согласуются с результатами, полученными с применением метода волновых функций, которые, в свою очередь, согласуются с экспериментальными данными. Вы должны позволить природе самой определять, что является разумным, а что — неразумным. Как написал в одной из своих работ Фейнман: «[Квантовая механика] дает совершенно абсурдное с точки зрения здравого смысла описание Природы. И оно полностью соответствует эксперименту. Так что я надеюсь, что вы сможете принять Природу такой, как Она есть — абсурдной»8'.

Однако независимо от того, насколько абсурдной является природа на уровне микромира, при переходе к нашим обычным масштабам любая теория должна приводить к привычным прозаичным событиям. Как показал Фейнман, для движения больших тел, таких как бейсбольные мячи, аэропланы или планеты, каждое из которых является огромным по сравнению с субатомными частицами, его правило определения весов различных траекторий гарантирует, что все траектории, кроме одной, взаимно сократятся при суммировании их вкладов. В действительности, когда дело касается движения классического тела, значение имеет только одна траектория из бесконечного их количества. И это именно та траектория, которая следует из ньютоновских законов движения. Вот почему в нашем повседневном мире нам кажется, что тела (такие, как брошенный в воздух мяч) следуют вдоль единственной, уникальной и предсказуемой траектории из начальной точки в пункт назначения. Но для объектов микромира фейнмановское правило назначения весов траекториям показывает, что свой вклад в движение объекта могут вносить (и часто вносят) многочисленные возможные траектории. Например, в эксперименте с двумя щелями некоторые из траекторий проходят через разные щели, приводя к образованию интерференционной картины. В микромире мы не можем гарантировать, что электрон пройдет только через одну щель или только через другую. Интерференционная картина и фейнманов-ская альтернативная формулировка квантовой механики недвусмысленно поддерживают друг друга.

Как разные мнения о книге или фильме могут оказаться полезными для понимания различных моментов этого произведения, так и различные подходы к квантовой механике помогают углубить понимание этой теории. Хотя предсказания метода волновых функций и фейнмановского суммирования по траекториям полностью согласуются друг с другом, в их основе лежат совершенно различные представления. Как мы увидим позднее, для разных приложений тот или иной подход может стать неоценимым средством объяснения.

К настоящему моменту у вас должно было появиться некоторое представление о волнующем новом образе мироздания согласно квантовой механике. Если вы еще не впечатлились от поразительных высказываний Бора, квантовые чудеса, о которых пойдет речь ниже, заставят вас, по крайней мере, испытать головокружение.

Квантовую механику трудно понять на интуитивном уровне, еще труднее, чем теорию относительности — для этого нужно начать мыслить подобно миниатюрному человечку, родившемуся и выросшему в микромире. Существует, однако, одно положение этой теории, которое может служить путеводителем для интуиции, своего рода пробным камнем, который отличает квантовую логику от классической. Это соотношение неопределенностей, открытое немецким физиком Вернером Гейзенбергом в 1927 г.

Это соотношение выросло из проблемы, с которой мы уже сталкивались выше. Мы установили, что процедура определения щели, через которую проходит каждый из электронов (т. е. определение положения электронов), неизбежно вносит возмущения в их последующее движение. Однако вспомним, что убедиться в присутствии другого человека можно разными способами — можно дать ему увесистый шлепок по спине, а можно нежно коснуться его. Тогда что мешает нам определить положение электрона с помощью «более нежного» источника света, который бы оказывал меньшее влияние на его дальнейшее движение? С точки зрения физики XIX в. это вполне возможно. Используя все более слабую лампу (и все более чувствительный датчик светового излучения), мы можем оказывать исчезающе малое влияние на движение электрона. Но квантовая механика демонстрирует изъян в наших рассуждениях. Известно, что уменьшая интенсивность источника света, мы уменьшаем количество испускаемых фотонов. Когда мы дойдем до излучения отдельных фотонов, мы уже не сможем далее уменьшать интенсивность света без того, чтобы не выключить его совсем. Это фундаментальный квантово-механический предел «нежности» нашего исследования. Таким образом, всегда существует минимальное возмущение, которое мы вносим в движение электрона путем измерения его положения.

Что ж, все это верно. Однако закон Планка говорит, что энергия единичного фотона пропорциональна его частоте (и обратно пропорциональна длине волны). Следовательно, используя свет все меньшей и меньшей частоты (и, соответственно, все большей длины волны), мы можем делать отдельные фотоны все более «нежными». Однако и здесь есть загвоздка. Когда волна направляется на объект, получаемая информация будет достаточной для того, чтобы определить положение объекта с некоторой неустранимой погрешностью, равной длине волны. Для того чтобы получить интуитивное представление об этом важном факте, представим, что мы пытаемся определить положение большой скалы, находящейся немного ниже уровня моря, по влиянию, которое она оказывает на проходящие морские волны. Приближаясь к скале, волны образуют замечательно упорядоченную последовательность следующих одни за другими гребней и впадин. После прохождения над скалой форма волн искажается — верный признак наличия подводной скалы. Но подобно самым мелким делениям на линейке, отдельный цикл волны, образованный гребнем и впадиной, является мельчайшей единицей в последовательности волн, поэтому, если мы наблюдаем только возмущение в движении волн, мы можем определить положение скалы лишь с точностью, равной одному волновому циклу, или длине волны. В случае света составляющие его фотоны представляют собой, грубо говоря, отдельные волновые циклы (при этом высота циклов определяется числом фотонов); следовательно, при определении положения объекта фотон дает точность, равную длине волны.

Таким образом, мы сталкиваемся со своего рода квантово-механической компенсацией. Если мы используем высокочастотный свет (малой длины волны), мы можем с высокой точностью определить положение электрона. Но высокочастотные фотоны несут очень большое количество энергии и поэтому вносят большие возмущения в скорость движения электронов. Если мы используем низкочастотный свет (большой длины волны), мы минимизируем его влияние на движение электрона, поскольку фотоны, составляющие этот свет, имеют относительно низкую энергию, но в этом случае мы вынуждены пожертвовать точностью определения положения электрона. Гейзенберг выразил все это в виде математического соотношения между точностью измерения положения электрона и точностью определения его скорости. Он установил, что эти величины обратно пропорциональны друг другу: большая точность в определении положения неизбежно ведет к большей погрешности в определении скорости, и наоборот. Что еще более важно, хотя мы и ограничили наше обсуждение одним конкретным способом определения местоположения электрона, согласно Гейзенбергу компромисс между точностью определения положения и скорости является фундаментальным фактом, который остается справедливым независимо от используемого оборудования и метода измерения. В отличие от теорий Ньютона и даже Эйнштейна, в которых движущаяся частица описывается ее положением и скоростью, согласно квантовой механике на микроскопическом уровне вы не можете знать оба этих параметра с одинаковой точностью. Более того, чем точнее вы знаете один параметр, тем больше погрешность другого. Хотя мы ограничили наше описание электронами, то же самое относится ко всем составным элементам мироздания.

Эйнштейн пытался минимизировать этот отход от позиций классической физики, утверждая, что хотя квантовая механика определенно ставит предел нашему знанию положения и скорости, электрон, тем не менее, имеет определенное положение и скорость в том смысле, который мы привыкли вкладывать в эти слова. Однако в течение последних двух десятилетий прогресс в теоретической физике, достигнутый группой исследователей, возглавляемых ирландским физиком Джоном Беллом, и экспериментальные данные Алана Аспекта и его коллег убедительно продемонстрировали, что Эйнштейн был не прав. Про электроны, как и про любые другие частицы, нельзя одновременно сказать, что они находятся в таком-то месте и имеют такую-то скорость. Квантовая механика показывает, что это утверждение не только не может быть проверено экспериментально (по причинам, объясненным выше), но оно, кроме того, прямо противоречит другим, совсем недавно полученным экспериментальным данным.

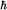В действительности происходит так: если вы поместите электрон в большую коробку и затем начнете медленно сдвигать ее стенки, чтобы определить его положение с увеличивающейся точностью, вы обнаружите, что движение электрона будет становиться все более и более неистовым. Электрон, будто охваченный своего рода клаустрофобией, будет возбуждаться все сильнее — отскакивая от стенок коробки со все возрастающей и непредсказуемой скоростью. Природа не позволяет загнать в угол свои компоненты. Как вы помните, в Н-баре, где мы сделали значение гораздо большим, чем оно есть в реальном мире, чтобы квантовые эффекты могли непосредственно влиять на объекты реального мира, кубики льда в напитках Джорджа и Грейс находились в неистовом движении, как будто тоже страдали от квантовой клаустрофобии. Хотя Н-бар является фантазией — в действительности значение исчезающе мало — точно такая же квантовая клаустрофобия является неотъемлемым свойством микромира. Движение микрочастиц становится все более хаотическим, по мере того как их положение ограничивается при исследовании все меньшими областями в пространстве.

Соотношение неопределенностей лежит в основе еще одного потрясающего явления, известного под названием квантового туннелирования. Если вы выстрелите пластиковой пулей в бетонную стенку толщиной в десять футов, то результат будет полностью соответствовать и вашим интуитивным представлениям, и классической физике: пуля отскочит назад. Причина состоит в том, что у пули просто недостаточно энергии, чтобы пробить такое прочное препятствие. Однако если перейти на уровень фундаментальных частиц, то, как совершенно определенно показывает квантовая механика, в волновую функцию (или, иначе, вероятностную волну) каждой составляющей пулю частицы заложена небольшая вероятность того, что эта частица может пройти сквозь стену. Это означает, что существует маленькая, но ненулевая, вероятность того, что пуля на самом деле сможет пройти сквозь стену и оказаться на другой стороне. Как такое может случиться? Причина снова содержится в соотношении неопределенностей Гейзенберга.

Чтобы понять это, представьте, что вы живете в полной нищете и вдруг узнаете, что ваш дальний родственник отошел в лучший мир, оставив вам огромное состояние. Единственная проблема состоит в том, что у вас нет денег для покупки билета на самолет. Вы объясняете ситуацию своим друзьям: если они помогут вам преодолеть барьер между вами и наследством, ссудив деньги на билет, вы вернете им долг с процентами после возвращения. Но ни у кого нет денег, чтобы дать вам в долг. Тут вы вспоминаете про вашего старого друга, который работает в авиакомпании, и обращаетесь к нему с той же просьбой. Он тоже не может дать вам денег взаймы, но предлагает другое решение. Система учета в авиакомпании такова, что если вы вышлете деньги в уплату за билет телеграфным переводом в течение 24 часов с момента прибытия в пункт назначения, никто не узнает, что вы не уплатили их до вылета.

Система учета в квантовой механике довольно схожа с этой. Показав, что существует компромисс между точностью измерения местоположения и скорости, Гейзенберг, кроме того, продемонстрировал существование компромисса между точностью измерения энергии и тем, сколько времени занимают эти измерения. Согласно квантовой механике вы не можете утверждать, что частица имеет в точности такую-то энергию в точно такой-то момент времени. За возрастающую точность измерения энергии приходится платить возрастающей продолжительностью проведения измерений. Грубо говоря, это означает, что энергия частицы может флуктуировать в очень широких пределах, если измерения проводятся в течение достаточно короткого периода времени. Поэтому точно так же как система учета в авиакомпании «позволяет» вам занять «деньги» на билет при условии, что вы вернете их достаточно быстро, квантовая механика «позволяет» частице «занять» энергию при условии, что она может вернуть ее в течение промежутка времени, определяемого сотношением неопределенностей Гейзенберга.

Математический аппарат квантовой механики показывает, что чем выше энергетический барьер, тем меньше вероятность того, что такой созидательный микроскопический переучет произойдет. Однако если говорить о микроскопических частицах, находящихся перед бетонной плитой, они имеют возможность занять достаточное количество энергии и иногда делают то, что с точки зрения классической физики является невозможным: они мгновенно проходят через область, для проникновения в которую у них раньше не хватало энергии. При переходе к более сложным объектам, состоящим из большего числа частиц, возможность квантового туннелирования сохраняется, но становится очень маловероятной, поскольку требует, чтобы все частицы совершили переход одновременно. Однако шокирующие эпизоды, подобные исчезновению сигары Джорджа, перемещению кубика льда сквозь стенку бокала и проход Джорджа и Грейс сквозь стенку бара, могут происходить. В фантастическом месте, подобном Н-бару, в котором значения велики, квантовое туннелирование является обычным делом. Однако квантовой механикой правят законы вероятности. В частности, малость значения в реальном мире означает, что если вы будете каждую секунду атаковать бетонную стену, вам придется потратить время, превышающее возраст Вселенной, прежде чем у вас появится сколько-нибудь заметный шанс пройти сквозь стену в одной из попыток. Однако, имея бесконечное терпение (и такую же продолжительность жизни), рано или поздно вы можете оказаться с другой стороны.

Соотношение неопределенностей является сердцевиной квантовой механики.

Свойства, которые кажутся нам обычно столь фундаментальными, что не вызывают никаких сомнений, — что объекты имеют определенное положение и скорость, и что в определенные моменты времени они имеют определенную энергию, — теперь представляются всего лишь следствием того, что постоянная Планка так мала в масштабах нашего повседневного мира. Первостепенное значение имеет то, что применение этих квантовых принципов к структуре пространства-времени демонстрирует фатальное несовершенство «основ гравитации» и приводит нас к третьему и наиболее серьезному противоречию, с которым столкнулись физики в течение последнего столетия.