"Элегантная вселенная (суперструны, скрытые размерности и поиски окончательной теории)" - читать интересную книгу автора (Грин Брайан)

Глава 11. Разрывая ткань пространства

Если непрерывно растягивать резиновую пленку, рано или поздно она порвется. Этот простой факт заставлял физиков годами обращаться к вопросу, возможно ли подобное по отношению к ткани пространства, создающего Вселенную. Может ли эта ткань разорваться, или такое вводящее в заблуждение представление есть результат слишком буквального понимания аналогии с резиновой пленкой?

Общая теория относительности Эйнштейна отвечает на вопрос о возможном разрыве структуры пространства отрицательно1'. Уравнения общей теории относительности основаны на римановой геометрии, которая, как отмечалось в предыдущей главе, позволяет проанализировать искажения свойств расстояний между соседними точками пространства. Чтобы формулы для расстояний были осмысленными, в математическом формализме требуется гладкость самого пространства. Понятие «гладкости» имеет конкретный математический смысл, но общеупотребительное значение слова «гладкость» хорошо передает суть этого понятия: гладкий — значит без складок, без проколов, без отдельных «нагроможденных» друг на друга кусков, без разрывов. Если бы в структуре пространства существовали такие нерегулярности, уравнения общей теории относительности нарушались бы, оповещая о космической катастрофе того или иного рода: зловещая перспектива, которую наша Вселенная благоразумно обходит.

Впрочем, эта зловещая перспектива не отпугивала склонных фантазировать теоретиков, которые годами исследовали возможность квантово-механического обобщения классической теории Эйнштейна, допускающего существование проколов, разрывов и слияний ткани пространства. Тот факт, что по законам квантовой физики на малых расстояниях происходят неистовые флуктуации, позволял предположить, что проколы и разрывы могут быть обычными явлениями в микроскопической структуре пространства. Понятие пространственно-временных червоточин (В русскоязычной литературе более распространенным является термин «кротовые норы». — Прим. ред.) (хорошо знакомое поклонникам фантастического сериала «Звездный путь») опирается на подобные предположения. Идея проста. Представим себе крупную корпорацию, управление которой находится на девяностом этаже одного из небоскребов. Исторически сложилось так, что отделение корпорации, с которым сотрудникам этого управления в последнее время все чаще приходится связываться, находится на девяностом этаже соседнего небоскреба. Так как переносить один из офисов в другое здание нецелесообразно, разумным решением было бы строительство моста, соединяющего две башни. Тогда сотрудники получили бы возможность переходить из офиса в офис, не спускаясь вниз и поднимаясь вверх на девяносто этажей.

Пространственно-временная червоточина играет схожую роль. Это мост или туннель, служащий укороченным маршрутом из одной области вселенной в другую. Пример червоточины в двумерной вселенной показан на рис. 11.1. Если управление «двумерной» корпорации находится вблизи нижней окружности рис. 11.1 а, то в ее отделение на верхней окружности можно попасть, лишь путешествуя по всему U-образному маршруту, ведущему из одного края вселенной в другой. Но если ткань пространства может рваться с образованием проколов, изображенных на рис. 11.1 б; если эти проколы могут «срастись» краями, как на рис. 11.1 в, то две ранее отдаленные области соединятся пространственным мостом. Это и есть червоточина. Нужно отметить, что хотя червоточина и мост между небоскребами имеют некоторое сходство, между ними есть и существенное различие. Мост между небоскребами пролегает по существующему пространству, т. е. по пространству между небоскребами. Червоточина, в отличие от этого, образует новое пространство, ибо изображенная на рис. 11.1 а двумерная искривленная поверхность — это все, что имелось. Область вне поверхности лишь артефакт неадекватной картинки, которая не может изобразить U-образную вселенную иначе как погруженной в наш трехмерный мир.

Рис. 11.1. а) «U-образная» вселенная, в которой достичь одного конца с другого можно лишь после длительного космического путешествия, б) Ткань пространства рвется, и два конца червоточины начинают вытягиваться, в) Два конца червоточины соединяются, образуя новый мост — «срезая путь» между двумя концами вселенной.

Червоточина создает новое пространство и потому прокладывает новую пространственную территорию. Существуют ли червоточины во Вселенной? Этого не знает никто. И если они действительно существуют, неясно, могут ли они быть только микроскопической формы, или перекрывать обширные области пространства, как в фантастических фильмах. Существование червоточин в реальном мире во многом определяется тем, возможен ли разрыв структуры пространства.

Другой яркий пример того, как ткань пространства может растягиваться до предела, дают черные дыры. На примере рис. 3.7 мы видели, что сильнейшее гравитационное поле черной дыры приводит к настолько сильной искривленности пространства, что оно выглядит проколотым в центре черной дыры. В отличие от червоточин, есть веские экспериментальные свидетельства в пользу существования черных дыр, и вопрос о том, что происходит в центре дыры, приобретает конкретный научный характер. В экстремальных условиях внутри черной дыры уравнения общей теории относительности становятся неприменимыми. По мнению некоторых физиков, в центре черной дыры действительно имеется прокол, но мы ограждены от этой космической «сингулярности» горизонтом событий, не позволяющим даже свету вырваться из гравитационной ловушки. Такие соображения привели Роджера Пенроуза из Оксфордского университета к «гипотезе космической цензуры», согласно которой подобные пространственные особенности возможны лишь в местах, тщательно скрытых от наших глаз пеленой горизонта событий. С другой стороны, до открытия теории струн некоторые физики считали, что корректное объединение квантовой теории и общей теории относительности «залатает» бросающиеся в глаза бреши в ткани пространства, сгладив его квантовыми поправками.

С открытием теории струн, органично связывающей квантовую теорию с гравитацией, появилась твердая почва для исследования этих вопросов. На сегодняшний день они окончательно не решены, но в последние годы были решены тесно связанные с ними вопросы. В этой главе мы покажем, что в теории струн впервые явно демонстрируется возможность разрыва ткани пространства при определенных физических явлениях (в некоторых отношениях отличных от явлений пространственных червоточин и черных дыр).

В 1987 г. Шин-Тун Яу и его студент Ганг Тиан, работающий сейчас в Массачусетсом технологическом институте, сделали интересное математическое наблюдение. Используя хорошо известный математический прием, они обнаружили, что одни многообразия Калаби-Яу можно преобразовать в другие путем протыкания их поверхности и сшивания образовавшегося отверстия согласно строго определенной математической процедуре2). Грубо говоря, они обнаружили, что внутри исходного пространства Калаби-Яу можно выделить двумерную сферу определенного вида (рис. 11.2). (Двумерная сфера аналогична поверхности надувного мяча, который, как и все знакомые нам объекты, трехмерен. Здесь, однако, мы говорим только о поверхности, не учитывая толщину материала, из которого сделан мяч, а также пространство внутри него. Точки на поверхности мяча определяются двумя числами, «широтой» и «долготой», аналогично тому, как определяются координаты на поверхности Земли. Вот почему поверхность мяча, как и поверхность упоминавшегося в предыдущих главах Садового шланга, является двумерной.)

Рис. 11.2. В выделенной области внутри пространства Калаби-Яу находится сфера.

Далее они рассмотрели стягивание сферы в одну точку; этот процесс показан на рис. 11.3. Как и все последующие рисунки этой главы, он упрощен с целью наглядности изображения наиболее важного «куска» пространства Калаби-Яу: но вы должны помнить, что такие преобразования происходят внутри несколько большего пространства Калаби-Яу, подобного изображенному на рис. 11.2.

Рис. 11.3. Сфера внутри пространства Калаби-Яу. сжимается в точку, приводя к перетяжке в ткани пространства. На этом и следующих рисунках для простоты показана лишь часть всего пространства Калаби-Яу

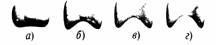И, наконец, Тиан и Яу рассмотрели случай, когда в точке сжатия пространство Калаби-Яу слегка надрывается (рис. 11.4 а), раскрывается и перестраивается в другую шарообразную фигуру (рис. 11.4 б), которую затем снова можно раздуть до нормального размера (рис. 11.4 в и 11.4 г).

Рис. 11.4. При разрыве перетяжки пространства Калаби-Яу возникает сфера, которая сглаживает его поверхность. Исходная сфера рис. 11.3 оказывается «перестроенной».

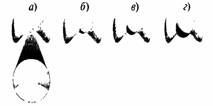Математики называют последовательность таких действий флоп-перестройкой (В оригинале flop-transition. Некоторые термины, используемые автором в этой и следующих главах, не являются общепринятыми (и/или еще не имеют русского эквивалента): мы подошли к обсуждению вопросов, касающихся последних достижений в физике и математике. — Прим. перев.)

Все происходит так, как будто надувной мяч «выворачивается» наизнанку внутри другого пространства Калаби-Яу. Тиан, Яу и другие математики показали, что при определенных условиях новое многообразие Калаби— Яу (см. рис. 11.4 г), будет топологически отличным от исходного (рис. 11.3 а). То есть, выражаясь привычным языком, не существует никакого способа деформировать исходное пространство Калаби-Яу, показанное на рис. 11.3 а, в конечное пространство Калаби-Яу, показанное на рис. 11.4 г, не разрывая на некотором промежуточном этапе структуры пространства Калаби-Яу.

С точки зрения математики процедура Яу и Тиана очень интересна, так как позволяет получить новые пространства Калаби-Яу из уже известных. Но действительная сила процедуры проявляется в области физики, где в этой связи возникает волнующий вопрос: если забыть об абстрактном характере данной математической процедуры, может ли в природе иметь место изображенная на рис. 11.3 а — 11.4 г последовательность превращений? Может ли произойти так, что вопреки предсказаниям теории Эйнштейна структура пространства способна рваться и затем восстанавливаться подобно тому, как описано выше?

На протяжении нескольких лет после 1987 г., когда Яу сделал свое наблюдение, он часто советовал мне поразмыслить о возможных физических применениях флоп-перестроек. Я отнекивался. Мне казалось, что флоп-перестройки относятся только к абстрактной математике и не имеют никакого отношения к теории струн. Действительно, из главы 10, в которой было установлено существование минимального радиуса циклического измерения, можно сделать вывод, что в теории струн сфера на рис. 11.3 не может полностью стянуться к выколотой точке. Однако, как тоже отмечено в главе 10, если стягивается часть пространства (в данном случае — сферическая часть многообразия Калаби— Яу), а не все циклическое измерение, то аргументы, которые позволяют различать малые и большие радиусы, не применимы буквально. Тем не менее, возможность разрыва структуры пространства казалась маловероятной, даже при том, что запрещающие флоп-перестройку соображения не выдерживали серьезной критики.

Уже позже, в 1991 г., норвежский физик Энди Люткен и мой однокурсник по учебе в Оксфорде, а ныне профессор университета Дьюка, Пол Аспинуолл, задались вопросом, который впоследствии оказался очень интересным. Если перестраивается пространственная структура компоненты Калаби-Яу нашей Вселенной, как это будет выглядеть с точки зрения зеркального пространства Калаби-Яу? Чтобы понять, почему возник такой вопрос, нужно вспомнить, что физические свойства зеркальной пары пространств Калаби-Яу (если эти пространства используются в качестве дополнительных измерений) идентичны, но сложность математических расчетов, необходимых для установления этих физических свойств, может сильно отличаться. Аспинуолл и Люткен предположили, что математически сложный переход между рис. 11.3 и 11.4 может описываться гораздо проще в терминах зеркальных пространств, и физический смысл этого перехода станет гораздо понятнее.

В момент проведения этих исследований еще не было достаточного понимания зеркальной симметрии, чтобы иметь возможность ответить на поставленный вопрос. И все же Аспинуолл и Люткен отметили, что в зеркальном описании нет ничего такого, что свидетельствовало бы об абсурдных физических последствиях разрывов пространства при флоп-перестройках. Примерно в то же время мы с Плессером, развивая найденную нами идею зеркальных пар многообразий Калаби-Яу (см. главу 10), неожиданно сами столкнулись с необходимостью анализа флоп-перестроек. Математикам хорошо известен тот факт, что склеивание различных точек (подобное показанному на рис. 10.4), которое использовалось нами для построения зеркальных пар, приводит к геометрическим следствиям, идентичным перетягиванию и проколам на рис. 11.3 и 11.4. В соответствующей физической формулировке мы с Плессером, однако, не нашли явных противоречий. Более того, вдохновленные результатами Аспинуолла и Люткена (а также результатом их предыдущей совместной работы с Грэмом Россом), мы пришли к выводу, что математически перетягивание можно «отреставрировать» двумя различными способами. Один из них приводит к пространству Калаби-Яу, соответствующему рис. 11.3 а, а другой — к пространству, соответствующему рис. 11.4 г. Это подсказало нам, что переход от рис. 11.3 а к рис. 11.4 г действительно может иметь место в реальном мире.

Таким образом, к концу 1991 г. у некоторых физиков, занимающихся теорией струн, возникло ясное ощущение того, что ткань пространства может разрываться. Но ни у кого из них не было технических методов, которые позволили бы твердо установить или опровергнуть справедливость этой замечательной гипотезы.

В течение 1992 г. мы с Плессером время от времени возвращались к попыткам доказать, что структура пространства может подвергаться перестройкам с разрывами пространства. Наши расчеты частично подтверждали эту гипотезу в частных случаях, но строгого доказательства найти не удавалось. Весной Плессер съездил с докладом в Принстонский институт перспективных исследований. Там он встретился с Виттеном и в частной беседе рассказал ему о наших попытках дать интерпретацию математической процедуры флоп-перестройки с разрывом пространства в рамках теории струн. После того, как Плессер изложил свои соображения, Виттен отвернулся от доски и некоторое время, возможно минуту или две, молча смотрел в окно своего кабинета. Затем он повернулся к Плессеру и сказал, что если наши идеи окажутся правильными, то «это будет впечатляюще». Такая реакция Виттена побудила нас работать с удвоенной энергией. Однако вскоре исследования застопорились, и мы обратились к другим вопросам в теории струн.

Даже работая над другими задачами, я постоянно ловил себя на том, что возвращаюсь к мысли о возможности перестроек с разрывами пространства. Месяц от месяца во мне укреплялась уверенность, что они должны быть неотъемлемой частью теории струн. Из расчетов, сделанных ранее вместе с Плессером, а также из стимулирующих обсуждений с Дэвидом Моррисоном, математиком университета Дьюка, казалось, следовало, что возможность перестроек является естественным следствием зеркальной симметрии. Во время моего пребывания в Дьюке Моррисон и я, используя результаты гостившего в то же время в Дьюке Шелдона Каца из Оклахомского университета, наметили стратегию обоснования появления флоп-перестроек в теории струн. Однако когда мы приступили к вычислениям, оказалось, что они крайне громоздки: даже с использованием самого быстрого в мире компьютера на расчеты ушла бы сотня лет. Мы продвигались вперед, но нам явно не хватало новой идеи, которая значительно повысила бы эффективность нашего вычислительного метода. Не подозревая об этом, Виктор Батырев, математик из университета города Эссен, дал нам такую идею в двух своих статьях, опубликованных весной и летом 1992 г.

Батырев очень интересовался зеркальной симметрией, особенно после успешного решения Канделасом и соавторами описанной в конце главы 10 задачи о подсчете числа сфер. Однако Батырев, будучи математиком, был сбит с толку приемами, которые мы с Плессером использовали для нахождения зеркальных пар пространств Калаби— Яу. Хотя в нашем подходе применялись известные теоретикам методы, Батырев позже признался мне, что наша статья произвела на него впечатление «черной магии». Это было следствием исторически сложившихся культурных различий между математикой и физикой, и по мере размытия теорией струн границ каждой науки различия в языке, методах и стиле исследований становились все более явными. Физики больше похожи на композиторов-авангардистов, стремящихся обойти устоявшиеся правила и расширить границы дозволенного при поиске решения задачи. Математики же больше похожи на классических композиторов, обычно скованных рамками гораздо более жесткой схемы и с неохотой воспринимающих переход к следующему шагу до тех пор, пока предыдущие шаги не были обоснованы со всей строгостью. У каждого подхода свои преимущества и недостатки, и каждый из них обладает своими уникальными возможностями для творческих исследований. Так же, как современную музыку нелепо сравнивать с классической, эти подходы нельзя сравнивать, чтобы выяснить, какой из них лучше — используемые методы в значительной степени определяются вкусами и подготовкой.

Батырев решил перевести схему построения зеркальных многообразий на более понятный математический язык, и это ему удалось. Под впечатлением белее ранней работы тайваньского математика Ши-Шир Роана, Батыреву удалось сформулировать последовательную математическую процедуру построения пар пространств Калаби-Яу, являющихся зеркальными близнецами друг друга. Его процедура сводится к нашей с Плессером, если применять ее для рассмотренных нами примеров, но приводит к более общей формулировке в терминах знакомых математикам понятий.

Оборотной стороной медали было то, что в работах Батырева использовались знания из неизвестных большинству физиков областей математики. Мне, например, удалось уловить суть его аргументов, но понимание многих важнейших моментов давалось с огромным трудом. Одно, тем не менее, было ясно: методы, описанные в его статье, при правильном их осознании и применении вполне могут дать второе дыхание исследованиям флоп-перестроек с разрывом пространства.

К концу лета, находясь под впечатлением результатов этих работ, я решил вернуться к задаче о флоп-перестройках и сконцентрировать на ней все свое внимание. От Моррисона я узнал, что он собирается провести год в Институте перспективных исследований, а Аспинуолл, по моим сведениям, тоже будет там на стажировке. После нескольких телефонных звонков и переписки по электронной почте я договорился, что тоже проведу осень 1992 г. в этом институте.

Трудно вообразить себе лучшее место для многочасовой и напряженной исследовательской работы, чем Институт перспективных исследований. Этот институт, основанный в 1930 г., расположен среди слегка холмистых полей, примыкающих к идиллическому лесу, и находится в нескольких милях от территории Принстонского университета. Говорят, здесь ничто не может отвлечь вас от работы в Институте, потому что отвлекать просто нечему.

После отъезда из Германии в 1933 г. Эйнштейн обосновался в этом институте и прожил здесь до конца своей жизни. Не нужно напрягать воображение, чтобы представить его размышляющим о единой теории поля в безлюдной тишине и почти аскетической атмосфере окрестностей Института. В воздухе здесь витает дух наследия прошлых глубоких идей, и ощущение этого может быть или возбуждающим, или угнетающим, в зависимости от того, на какой промежуточной стадии находятся ваши исследования.

Как-то раз, вскоре после моего прибытия в Институт, мы с Аспинуоллом прогуливались по улице Нассау (главной торговой улице в Принстоне), рассуждая о том, где будем сегодня обедать. Вопрос не праздный, потому что Поль — большой любитель мясного, а я вегетарианец. В самый разгар обмена мнениями о стилях жизни он спросил, есть ли у меня идеи о том, какими новыми задачами стоило бы заняться. Я ответил, что есть, и подробно изложил свои соображения по поводу важности вопроса о том, возможны ли во Вселенной флоп-перестройки с разрывом пространства, если Вселенная действительно описывается теорией струн. Я также обрисовал ему стратегию своих действий и рассказал о недавно возникшей надежде на то, что работа Батырева может помочь восполнить недостающие пробелы в понимании. Я полагал, что проповедую новообращенному, и Поль будет возбужден перспективой этого исследования. Но я ошибся. Сейчас, задним числом, я понимаю, что его сдержанность объяснялась добродушной и давно возникшей тягой к интеллектуальному соперничеству, в котором каждый из нас играет роль «адвоката дьявола» по отношению к идеям другого. Не прошло и нескольких дней, как он примкнул ко мне, и мы оба с головой погрузились в изучение флоп-перестроек.

К тому времени приехал и Моррисон. Втроем мы собрались в институтском кафе, чтобы выработать план действий. Мы были единодушны в том, что главная задача состоит в ответе на вопрос, могут ли переходы от рис. 11.3 а к рис. 11.4 г иметь место в нашей Вселенной. Однако решение этой задачи в лоб сулило непреодолимые препятствия, так как описывающие этот переход уравнения, особенно те из них, которые описывают разрыв пространства, крайне сложны. Вместо этого, мы решили переформулировать задачу в терминах зеркальных пространств, надеясь на то, что уравнения в этом случае будут более простыми. Идея схематически показана на рис. 11.5, где в верхнем ряду показана эволюция от рис. 11.3 а к рис. 11.4 г, а в нижнем — та же эволюция с точки зрения зеркальных многообразий Калаби-Яу.

Рис. 11.5. Флоп-перестройка с разрывом пространства (верхний ряд) и соответствующая зеркальная формулировка (нижний ряд).

Уже тогда нам было ясно, что в зеркальной формулировке физика струн обладает хорошими свойствами и свободна от всякого рода катастроф. На рис. 11.5 видно, что в нижнем ряду не наблюдается разрывов или проколов пространства. Однако самый сложный вопрос, к которому привело нас это наблюдение, заключался в том, не переходим ли мы через границы применимости зеркальной симметрии. И, несмотря на то, что верхние и нижние многообразия Калаби-Яу, изображенные в левой колонке на рис. 11.5, приводят к эквивалентным физическим результатам, верно ли, что на каждом шаге вправо, изображенном на рис. 11.5 (в процессе чего в середине обязательно встретятся фазы прокола-разрыва-восстановления) физические свойства исходной и зеркальной точки зрения идентичны?

Хотя у нас были достаточные основания считать, что важная связь между исходными и зеркальными многообразиями не нарушится в ходе преобразований, приводящих к разрыву пространства Калаби-Яу в верхней части рис. 11.5, мы понимали, что вопрос о том, останутся ли многообразия на рис. 11.5 зеркальными друг другу после разрыва, нетривиален. Это ключевой вопрос, так как если они останутся зеркальными, отсутствие катастрофы в зеркальной формулировке будет означать отсутствие катастрофы в исходной формулировке, и это станет доказательством того, что пространство в теории струн может разрываться. Мы поняли, что этот вопрос можно свести к вычислению. Нужно рассчитать физические свойства Вселенной для верхнего многообразия Калаби-Яу после разрыва (например, используя правое верхнее пространство Калаби-Яу на рис. 11.5) и физические свойства зеркального (по предположению) пространства (правого нижнего пространства Калаби-Яу на рис. 11.5), а затем сравнить, будут ли эти свойства одинаковы.

Этим расчетом Аспинуолл, Моррисон и я занимались осенью 1992 г.

Острый, как лезвие бритвы, ум Эдварда Виттена облечен в мягкие манеры, что часто приобретает насмешливый, почти иронический оттенок. Виттен общепризнанно считается наследником титула Эйнштейна в роли величайшего из живущих на Земле физиков. Некоторые даже считают его величайшим физиком всех времен. У Виттена неутолимая жажда к передовым исследованиям в физике, а его влияние на выбор направлений исследования в теории струн огромно.

Работоспособность Виттена стала легендой. По словам его жены Кьяры Наппи, которая занимается физикой в том же институте, Виттен часами сидит на кухне, мысленно анализируя передовые достижения в теории струн и лишь изредка возвращаясь в комнату за ручкой и бумагой, чтобы проверить одну или две тонкие детали3). Другую историю рассказал стажер, которого как-то летом разместили в соседнем с Виттеном кабинете. Он описывал свое уныние, когда он часами мучился со сложными расчетами в теории струн под ритмичный и непрекращающийся стук клавиш из кабинета Виттена, свидетельствовавший о том, что прямо из головы Виттена в файлы на компьютере одна за другой струятся статьи, которые вскоре сыграют поворотную роль в науке.

Примерно через неделю после моего приезда, когда мы с Виттеном беседовали в институтском дворике, он справился о моих научных планах. Я рассказал ему о флоп-перестройках с разрывами пространства и о стратегии, которую мы в этой связи избрали. Услышав об этих идеях, Виттен крайне заинтересовался, но предупредил, что, по его мнению, расчеты будут чрезвычайно сложными. Он также отметил потенциально слабое звено в описанной стратегии, которое относилось к моей совместной работе с Вафой и Уорнером, проделанной несколькими годами ранее. Вопрос, который поднял Виттен, имел лишь косвенное отношение к нашему подходу, но этот вопрос побудил его заняться задачей, которая, в конце концов, оказалась связанной с нашими задачами и дополнительной по отношению к ним.

Аспинуолл, Моррисон и я решили разбить вычисления на два этапа. Естественное на первый взгляд разделение состояло в вычислении сначала физических характеристик, соответствующих последнему многообразию Калаби-Яу в верхнем ряду рис. 11.5, а затем характеристик, соответствующих последнему многообразию в нижнем ряду рис. 11.5. Если зеркальность не нарушается в результате разрыва для верхнего ряда, то эти два многообразия должны приводить к одинаковым физическим следствиям, так же, как к одинаковым следствиям приводит анализ двух исходных многообразий. (В такой постановке задачи не требуется проведения крайне сложных вычислений для верхнего многообразия в момент его разрыва.) Оказалось, что вычисления физических характеристик для последнего из верхнего ряда многообразий Калаби-Яу достаточно просты. Главная сложность состояла в том, чтобы сначала определить точный вид последнего многообразия Калаби-Яу в нижнем ряду на рис. 11.5 (которое, по предположению, является зеркальным образом верхнего многообразия), а затем получить для него соответствующие физические результаты.

Процедура решения второй задачи, т. е. вычисления физических характеристик последнего из многообразий Калаби-Яу в нижнем ряду, если известна его точная геометрическая форма, была разработана несколькими годами ранее Канделасом. Его подход, однако, подразумевал проведение длительных расчетов. Мы поняли, что для решения задачи в данном конкретном случае нужно написать хорошую компьютерную программу. Аспинуолл, — не только известный физик, но и крутой программист, — взял эту задачу на себя. Моррисон и я приступили к расчету первой задачи о нахождении точного вида пространства Калаби-Яу.

Мы чувствовали, что именно в этом месте работа Батырева может подсказать нам ряд важных моментов. Однако и на этот раз исторически сложившиеся культурные различия в подходах математиков и физиков, — в данном случае, Моррисона и меня, — стали тормозить продвижение вперед. Нам нужно было соединить мощь двух наук и найти математический вид нижних многообразий Калаби-Яу, которые соответствуют той же физической Вселенной, что и верхние многообразия, если флоп-перестройки с разрывами на самом деле имеют место в действительности. Но ни я, ни Моррисон не знали чужого языка достаточно хорошо для того, чтобы ясно увидеть путь к достижению этой цели. Стало очевидным, что и мне, и ему нужно срочно пройти курс в области, экспертом в которой является другой из нас. Поэтому днем мы решили с максимальной отдачей пытаться двигаться вперед в наших расчетах, а по вечерам по очереди играть друг для друга роли преподавателя и студента: я буду в течение часа или двух читать лекции для Моррисона по интересующим нас физическим вопросам, а затем он в течение часа или двух будет читать мне лекции по соответствующим математическим вопросам. Эти лекции обычно заканчивались около 11 вечера.

Мы стали твердо соблюдать такой ежедневный режим. Продвижение было медленным, но мы чувствовали, что все начинает понемногу вставать на свои места. Тем временем Виттен семимильными шагами двигался к разрешению вопроса о слабом звене, которое он обнаружил ранее. В его работе предлагался новый мощный метод, связывающий физические результаты в теории струн с математическими аспектами пространств Калаби-Яу. Аспинуолл, Моррисон и я почти ежедневно участвовали в импровизированных дискуссиях с Виттеном, и он рассказывал нам о новых перспективах, которые открываются в его подходе. С каждой неделей становилось все яснее, что его работа, основанная на совершенно ином подходе, с неожиданной стороны приближается к вопросу о флоп-перестройках. Аспинуолл, Моррисон и я поняли, что если мы в ближайшее время не закончим наши вычисления, Виттен отправит всех нас в нокаут.

Ничто так благотворно не действует на мозг физика, как доза здорового соперничества. Аспинуолл, Моррисон и я вошли в азарт. Нужно отметить, что для Аспинуолла это означало одно, а для нас с Моррисоном совершенно другое. В характере Аспинуолла своеобразно сочетаются утонченность английского аристократа, во многом благодаря десяти годам студенчества и аспирантуры в Оксфорде, и озорное плутовство. Режим, в котором он работает, делает его одним из самых дисциплинированных физиков, которых я когда-либо знал. В то время как многие из нас засиживаются допоздна, Аспинуолл никогда не работает позже пяти часов вечера. В то время как многие из нас работают по выходным, Аспинуолл никогда этого не делает. Он чинно откланивается, потому что к этому моменту он успевает сделать все. Для него войти в азарт означает еще выше поднять планку эффективности своей работы.

Было начало декабря. Моррисон и я к тому времени обучали друг друга уже несколько месяцев, и это обучение начало себя оправдывать. Мы были очень близки к тому, чтобы установить точный вид искомого пространства Калаби-Яу. Более того, Аспинуолл почти закончил писать свою компьютерную программу и ждал нашего результата, который должен был служить ее начальными данными. Ночью в четверг нам с Моррисоном, наконец, стало совершенно ясно, как можно определить вид искомого пространства Калаби-Яу. Это сводилось к некоторой процедуре, которая также требовала своей (довольно простой) компьютерной программы. К полудню пятницы мы написали и отладили программу, а к позднему вечеру у нас на руках был результат.

Но это была пятница, и уже перевалило за 5 пополудни. Аспинуолл ушел домой, и не вернется до понедельника. Мы оказались в ситуации полного бессилия без его компьютерной программы. Но ни Моррисон, ни я и в мыслях не могли представить, что придется ждать все выходные: мы стояли на пороге решения вопроса о разрывах структуры пространства мироздания, мучившего нас столько времени, и бездействие было невыносимым. Мы позвонили Аспинуоллу домой и стали упрашивать его прийти в офис завтра утром. Сначала он решительно отказался. Но после долгого ворчания в трубку он все же согласился присоединиться к нам, если мы ему принесем блок из шести банок пива. Мы согласились.

Как и планировалось, мы встретились в Институте в субботу утром. Ярко светило Солнце, и настроение у всех было шутливо-расслабленным. Я был наполовину уверен, что Аспинуолл так и не появится, а когда он все же пришел, минут пятнадцать пел ему дифирамбы по поводу первого в его жизни прихода в офис в выходной день. Он заверил меня, что это больше не повторится.

Мы все сгрудились вокруг компьютера Моррисона, стоявшего в нашем кабинете. Аспинуолл объяснил Моррисону, как запустить программу и какой точный вид должны иметь вводимые в нее данные. Моррисон привел полученные ночью результаты к нужному виду, и теперь все было готово.

Расчет, который нужно было провести, грубо говоря, сводился к определению массы конкретной частицы, являющейся колебательной модой струны при ее движении во вселенной, компоненту Калаби-Яу которой мы изучали всю осень. Мы надеялись, что в соответствии с выбранной нами стратегией масса окажется точно такой же, что и масса в случае многообразия Калаби-Яу, возникшего после флоп-перестройки с разрывом пространства. Последнюю массу вычислить было легко, и мы сделали это несколькими неделями раньше. Ответ оказался равным 3 в определенной системе единиц, которой мы пользовались. А так как сейчас проводился численный расчет на компьютере, то ожидаемый результат должен был быть близким к числу 3, что-то вроде 3,000001 или 2,999999; отличие от точного ответа объяснялось бы ошибками округления.

Моррисон сел за компьютер. Его палец завис над клавишей «Enter». Напряжение нарастало. Моррисон выдохнул «поехали» и запустил программу. Через пару секунд компьютер выдал ответ: 8,999999. Мое сердце упало. Неужели действительно флоп-перестройки с разрывом пространства нарушают зеркальную симметрию, а значит, вряд ли существуют в реальности? Но в следующее же мгновение мы сообразили, что здесь какая-то глупая ошибка. Если в массах частиц на двух многообразиях действительно есть отличие, почти невероятно, что компьютер выдал бы результат, столь близкий к целому числу. Если наши идеи неверны, то с тем же самым успехом компьютер мог бы выдать ответ, состоящий из совершенно случайных цифр. Мы получили неправильный ответ, но неправильность его была такого вида, из которого напрашивался вывод о том, что где-то мы допустили банальную ошибку. Аспинуолл и я подошли к доске, и моментально ошибка была найдена: мы забыли множитель 3 в «простом» вычислении несколько недель назад, так что правильный результат должен был равняться 9. Поэтому ответ компьютера — это как раз то, на что мы надеялись.

Конечно, совпадение результата после того, как найдена ошибка, является лишь наполовину убедительным. Если известен желаемый результат, очень легко найти способ его получить. Нам срочно требовался другой пример. Имея все необходимые программы, придумать его не представляло сложности. Мы вычислили массу еще одной частицы на верхнем многообразии Калаби-Яу, на этот раз с особой тщательностью, чтобы избежать еще одной ошибки. Ответом было число 12. Мы снова окружили компьютер и запустили программу. Через несколько секунд был получен ответ 11,999999. Согласие. Мы доказали, что предполагаемое зеркальное пространство является зеркальным пространством, и флоп-перестройки с разрывами пространства являются частью теории струн.

Я вскочил со стула и, опьяненный победой, сделал круг по комнате. Моррисон, сияя, сидел за компьютером. И только реакция Аспинуолла была нестандартной. «Здорово. Я и не сомневался, что все так и будет, — спокойно сказал Аспинуолл. — А где мое пиво?»

В понедельник мы с победоносным видом направились к Виттену, чтобы сообщить ему о нашем успехе. Он был очень рад нашему результату. Оказалось, что он тоже только что нашел способ доказательства существования флоп-перестроек в теории струн. Его аргументация была совершенно иной и значительно проясняла понимание того, почему пространственные разрывы на микроскопических масштабах не приводят к катастрофическим последствиям.

Подход Виттена акцентирует различие между теорией точечных частиц и теорией струн в случае таких разрывов. Суть различия в том, что вблизи разрыва возможны два типа движения струны и только один тип движения точечной частицы. А именно, струна может двигаться, примыкая к разрыву, как и точечная частица, но, кроме того, она может опоясывать разрыв при движении, — что недоступно для точечной частицы, — как показано на рис. 11.6.

Рис. 11.6. Мировая поверхность, заметаемая струной, служит экраном, который гасит потенциально катастрофические эффекты при разрыве структуры пространства.

В результате опоясывания области разрыва струна экранирует окружающую ее Вселенную от катастрофических последствий, которые имели бы место в противном случае. В теории струн все происходит так, как будто мировая поверхность струны (двумерная поверхность, которую заметает струна при ее движении в пространстве, см. главу 6) эффективно играет роль барьера, на котором все пагубные воздействия геометрического вырождения пространства в точности сокращаются.

Здесь читатель вправе задать вопрос. Что будет, если разрыв действительно произойдет, но поблизости не окажется струн, которые экранировали бы его? Насколько эффективную защиту от этой кластерной бомбы, взрывающейся в момент разрыва пространства, может дать бесконечно тонкая «броня» струны? Ответ на оба вопроса основан на важнейшем квантово-механическом эффекте, рассмотренном в главе 4. Там было показано, что в фейнмановской формулировке квантовой механики объект, будь то струна или частица, движется от одной точки к другой, «разведывая» все возможные траектории. Наблюдаемое в результате движение есть объединение всех возможностей, и отдельные вклады каждой возможной траектории в движение точно определяются формулами квантовой механики. Если структура пространства внезапно разорвется, то среди всех возможных траекторий движущихся струн окажутся и те, которые опоясывают место разрыва (см. рис. 11.6). И хотя кажется, что около разрыва может не оказаться струн, в квантовой механике учитываются все возможные их траектории, и среди таких траекторий многие (в действительности, бесконечное число) будут опоясывать место разрыва. Виттен показал, что вклады именно этих траекторий сокращают эффект космической катастрофы, к которой привел бы разрыв пространства.

В январе 1993 г. Виттен и мы втроем одновременно послали наши работы в электронный архив статей в Интернете, из которого статьи моментально становятся доступными во всем мире. В наших статьях, основанных на двух совершенно различных точках зрения, приводились первые примеры переходов с изменением топологии — такое название мы дали процедуре с разрывом пространства. Давний вопрос о том, могут ли происходить разрывы пространства, был разрешен теорией струн и подтверждался количественными расчетами.

Мы добились большого успеха в понимании того, как могут происходить разрывы пространства без катастрофических физических последствий. Но что на самом деле происходит при таких разрывах? Какие следствия разрыва могут быть наблюдаемыми? Мы видели, что многие свойства окружающего нас мира зависят от конкретной структуры свернутых измерений. Поэтому естественно предположить, что радикальное изменение пространства Калаби-Яу при преобразовании, показанном на рис. 11.5, будет иметь серьезные физические последствия. Однако на самом деле на двумерных иллюстрациях, которыми мы пользуемся для того, чтобы представить себе пространства, картина происходящего в действительности преобразования несколько усложнена. Если бы нам удалось наглядно изобразить шестимерную геометрию, мы бы увидели, что структура пространства действительно рвется, но не так уж сильно. Повреждения больше похожи на изящные следы, оставляемые молью на пальто, чем на результат резкого приседания в брюках, из которых вы давно выросли.

В нашей работе, как и в работе Виттена, показано, что физические характеристики (например, число семейств струнных мод и типы частиц каждого семейства) не изменяются в ходе этих процессов. То, что может действительно меняться при преобразованиях пространства Калаби-Яу, на промежуточном этапе которых происходит разрыв, это массы отдельных частиц, т. е. энергии возможных мод колебаний струны. В наших работах было показано, что эти массы будут непрерывно изменяться в ответ на изменение геометрического вида компоненты Калаби-Яу, причем некоторые будут увеличиваться, а некоторые — уменьшаться. Важно, однако, то, что при разрыве не возникнет катастрофических скачков или других резких изменений значений меняющихся масс. С точки зрения физики момент разрыва пространства ничем не примечателен.

Здесь возникают два вопроса. Во-первых, мы рассматривали разрывы структуры пространства в дополнительном шестимерном пространстве Калаби-Яу. Могут ли эти разрывы возникать в трех наблюдаемых нами измерениях Вселенной? Почти наверняка могут. Пространство есть пространство, независимо от того, является оно туго скрученным в многообразие Калаби-Яу или развернутым до вселенских просторов, обширность которых мы понимаем, глядя лунной ночью на звездное небо. На самом деле, как мы видели, привычные нам пространственные измерения могут сами быть свернуты в гигантскую фигуру, замыкающуюся саму на себя в направлении другого конца Вселенной, и поэтому само деление измерений на свернутые и развернутые несколько искусственно. Хотя наш анализ, как и анализ Виттена, опирался на определенные математические свойства многообразий Калаби-Яу, тот результат, что структура пространства может разрываться, несомненно, имеет более широкие рамки применимости.

Во-вторых, может ли разрыв с изменением топологии произойти сегодня или завтра? Мог ли он иметь место в прошлом? Да. Экспериментальные исследования показывают, что массы элементарных частиц довольно стабильны во времени. Но на ранних стадиях после Большого взрыва даже в теориях, отличных от теории струн, рассматриваются важные периоды, в течение которых массы элементарных частиц менялись. С точки зрения теории струн в эти периоды, несомненно, происходили переходы с изменением топологии, рассмотренные в этой главе. Говоря о временах более близких к настоящему моменту, наблюдаемая стабильность масс элементарных частиц означает, что если сейчас Вселенная находится на стадии перехода с изменением топологии, то он происходит настолько медленно, что влияние на массы элементарных частиц невозможно зарегистрировать на современных экспериментальных установках. Примечательно, что пока выполняется это условие, наша Вселенная может находиться в данный момент в кульминации пространственного разрыва. Если разрыв происходит достаточно медленно, мы даже не поймем, что он происходит. Это один из редких примеров в физике, когда отсутствие поразительного экспериментально наблюдаемого феномена есть повод для сильного возбуждения. Отсутствие наблюдаемых катастрофических последствий при таком экзотическом изменении геометрии демонстрирует, как далеко продвинулась теория струн по сравнению с ожиданиями Эйнштейна.