"Элегантная вселенная (суперструны, скрытые размерности и поиски окончательной теории)" - читать интересную книгу автора (Грин Брайан)

Глава 7. «Супер» в суперструнах

Когда в ходе экспедиции Эддингтона 1919 г., организованной для проверки предсказаний Эйнштейна об отклонении света звезд Солнцем, был получен положительный результат, голландский физик Хендрик Лоренц известил об этом Эйнштейна телеграммой. Когда содержание телеграммы, подтверждающей общую теорию относительности, распространилось по всему миру, один студент задал Эйнштейну вопрос, о чем бы он подумал, если бы эксперимент Эддингтона не обнаружил предсказанного отклонения лучей света звезд. Эйнштейн ответил: «Мне было бы жаль Всевышнего, поскольку теория верна»1). Конечно же, если бы эксперименты действительно не подтвердили предсказаний Эйнштейна, его теория была бы признана неверной, и общая теория относительности не стала бы одним из столпов, на которых покоится современная физика. На самом деле Эйнштейн имел в виду, что общая теория относительности описывает гравитацию с таким изяществом, используя такие простые и в то же время мощные идеи, что он не мог себе представить, как природа могла пройти мимо этой возможности. С точки зрения Эйнштейна общая теория относительности была слишком красивой, чтобы оказаться неверной.

Однако эстетические аргументы не решают научных споров. В конечном счете, истинность физических теорий проверяется тем, насколько успешно они объясняют бесстрастные и упрямые экспериментальные данные. Однако к этому последнему утверждению есть одна очень важная оговорка. Когда теория находится в стадии разработки, ее неполнота часто не позволяет детально установить все ее экспериментальные следствия. Тем не менее, физики должны определить свой выбор и указать направления, в которых будут развиваться исследования такой незавершенной теории. Некоторые из этих решений диктуются внутренней логической непротиворечивостью; мы определенно требуем, чтобы любая разумная теория не содержала логически абсурдных положений. Другие решения обусловлены преимуществами одних теоретических конструкций над другими с точки зрения их следствий для экспериментальных исследований; обычно нас мало интересуют теории, содержимое которых не имеет отношения ни к чему, с чем мы сталкиваемся в окружающем нас мире. Однако, несомненно, бывают случаи, когда решения, принимаемые физиками-теоретиками, основываются на эстетических соображениях, на ощущении того, что красота и элегантность той или иной теории соответствует красоте и элегантности окружающего нас мира. Конечно, нет никаких гарантий, что такие соображения приведут нас к истине. Может быть, глубоко в своей основе структура мироздания менее элегантна, чем та, которую подсказывает наш опыт. Или, возможно, мы обнаружим, что современные эстетические критерии потребуют существенного пересмотра для применения в менее привычных условиях. Тем не менее, всегда и особенно сегодня, когда мы вступаем в эру, где наши теории описывают такие сферы мироздания, которые все труднее поддаются экспериментальному изучению, физики будут рассчитывать на то, что подобные эстетические соображения помогут избежать тупиковых направлений. До настоящего времени такой подход не раз демонстрировал свою мощь и предсказательную силу.

В физике, как и в искусстве, одну из ключевых ролей в эстетических принципах играет симметрия. Однако в отличие от искусства, в физике понятие симметрии имеет очень конкретный и точный смысл. На самом деле, аккуратно облекая это точное понятие симметрии в математическую форму, в течение последних нескольких десятилетий физики смогли разработать теории, в которых частицы вещества и частицы, передающие взаимодействие, переплетены более тесно, чем это считалось возможным когда-либо ранее. Подобные теории, объединяющие не только существующие в природе взаимодействия, но и материальные компоненты, имеют максимально возможную степень симметрии. По этой причине такие теории получили название суперсимметричных. Как мы увидим ниже, теория суперструн является одновременно предтечей и кульминацией суперсимметричных моделей.

Вообразим себе Вселенную, в которой законы физики являются такими же недолговечными, как и течения в моде, меняясь от года к году, день ото дня или даже от мгновения к мгновению. Можно утверждать наверняка, что если эти изменения не нарушат основных жизненных процессов, в таком мире вам некогда будет скучать. Простейшие действия превратятся в захватывающие приключения, поскольку случайные изменения законов природы не позволят вам или кому-либо еще использовать прошлый опыт для предсказания будущего.

Такая Вселенная была бы кошмаром для физика. Физики, как и большинство остальных людей, полагаются на стабильность мироздания: законы, которые истинны сегодня, были истинны вчера и останутся истинными завтра (даже если мы не настолько умны, чтобы понимать все эти законы). В конце концов, какой смысл следует вкладывать в слово «закон», если он может меняться столь незакономерно? Сказанное не означает, что Вселенная статична; Вселенная, несомненно, изменяется самым разнообразным образом от одного момента времени к другому. Скорее, это означает, что законы, управляющие подобной эволюцией, постоянны и неизменны. Возникает вопрос: действительно ли мы знаем, что это верно? На самом деле, не знаем. Однако наши успехи в описании многочисленных особенностей устройства мироздания, начиная от первого момента после Большого взрыва и по сегодняшний день, дают уверенность в том, что если законы природы и изменяются, то они должны делать это очень медленно. Простейшее предположение, согласующееся с тем, что нам известно на сегодняшний день, состоит в том, что законы природы неизменны. Теперь представим себе Вселенную, в разных частях которой свои законы физики, и эти законы, как местные обычаи, изменяются непредсказуемым образом от места к месту и отчаянно сопротивляются любому внешнему влиянию. Путешествие в таком мире, подобно приключениям Гулливера, заставит вас столкнуться с огромным разнообразием непредвиденных ситуаций. Однако с точки зрения физика это опять будет кошмаром. Очень трудно, например, примириться с фактом, что законы, которые действуют в одной стране — или даже в одном штате, — могут не действовать в другом. Но попробуйте представить, что произойдет, если таким же образом будут меняться законы природы. В таком мире эксперименты, проведенные в одном месте, не дадут никакой информации о физических законах, действующих в других местах. Физики должны будут снова и снова повторять свои эксперименты в разных местах, чтобы установить характер действующих там физических законов. К счастью, все, что мы знаем на сегодняшний день, говорит о том, что повсеместно действуют одни и те же законы физики. Эксперименты, проводимые по всему миру, могут быть объяснены на основе одних и тех же физических принципов. Более того, наша способность объяснить многочисленные астрофизические наблюдения, относящиеся к самым удаленным уголкам Вселенной, используя один и тот же неизменный набор физических принципов, заставляет нас верить в то, что действительно повсюду правят одни и те же физические законы. Поскольку мы никогда не бывали на противоположном краю Вселенной, мы не можем исключить возможность того, что где-то физика имеет совершенно иной характер, но все известные нам данные заставляют отвергнуть такой вариант.

Опять же, сказанное не означает, что Вселенная выглядит одинаково или что детали ее устройства одинаковы в разных местах. Космонавт, скачущий по Луне на «кузнечике» (палке с пружиной), способен проделать массу вещей, которые невозможно себе представить на Земле. Но мы понимаем, что это различие связано с тем, что Луна имеет гораздо меньшую массу, чем Земля; это вовсе не означает, что закон гравитации изменяется от одного места к другому. Ньютоновский или, точнее, эйнштейновский закон гравитации является одинаковым и для Земли, и для Луны. Различия в опыте космонавтов связаны с изменением обстановки, а не с изменением физических законов.

Физики называют эти два свойства физических законов, а именно то, что они не зависят от того, когда или где мы их применяем, симметриями природы. Используя этот термин, физики имеют в виду, что природа трактует каждый момент во времени и каждую точку в пространстве идентично, симметрично, гарантируя, что будут действовать одни и те же фундаментальные законы. Подобно их действию в живописи и в музыке, такие виды симметрии вызывают глубокое удовлетворение: они подчеркивают порядок и согласие в функционировании мироздания. Элегантность, с которой богатые, сложные и разнообразные явления вытекают из простого набора универсальных законов, составляет немалую часть того, что имеют в виду физики, используя слово «прекрасный».

В нашем обсуждении, посвященном специальной и общей теории относительности, мы столкнулись и с другими видами симметрии в природе. Вспомним, что принцип относительности, который лежит в основе специальной теории относительности, гласит, что законы физики будут одинаковы для наблюдателей, движущихся равномерно относительно друг друга. Этот принцип представляет собой разновидность симметрии, поскольку он означает, что природа относится к наблюдателям совершенно одинаково, симметрично. Каждый такой наблюдатель имеет право считать, что он находится в состоянии покоя. Подчеркнем еще раз, что это не означает идентичности картины, которую будут видеть разные наблюдатели; как мы показали ранее, их наблюдения могут существенно расходиться. Дело не в этом. Подобно различиям в ощущениях энтузиастов прыжков на палках с пружиной на Земле и на Луне, различия в наблюдениях отражают особенности обстановки, в которой проводились наблюдения, ведь наблюдатели находились в относительном движении. Но то, что они наблюдали, управлялось одними и теми же законами.

Открыв принцип эквивалентности, основу общей теории относительности, Эйнштейн значительно расширил этот тип симметрии. Он показал, что законы физики в действительности идентичны для всех наблюдателей, даже для тех, которые находятся в состоянии сложного ускоренного движения. Вспомним, что Эйнштейн придал этой идее законченный вид, осознав, что ускоряющийся наблюдатель имеет полное право считать, что он находится в состоянии покоя, утверждая, что сила, действующая на него, обусловлена гравитационным полем. После включения в данную систему гравитации все возможные точки зрения становятся абсолютно равноправными. Помимо несомненной эстетической привлекательности такой равноправной трактовки всех видов движения, эти принципы симметрии, как мы видели выше, играют ключевую роль в поразительных выводах о характере гравитации, к которым пришел Эйнштейн.

Есть ли еще принципы симметрии, имеющие дело с пространством, временем и движением, которым должны удовлетворять законы физики? Если вы основательно поразмыслите об этом, то сможете указать еще один принцип. Законы физики не должны зависеть от того, под каким углом вы проводите свои наблюдения. Например, если вы проводите какой-то эксперимент и после этого решаете повернуть вашу установку и повторить опыт, должны действовать те же самые законы. Этот принцип известен под названием вращательной симметрии, он означает, что законы физики трактуют все возможные направления как равноправные. Данный принцип симметрии имеет такое же значение, как и рассмотренные выше.

Существуют ли какие-либо еще принципы симметрии? Не пропустили ли мы какой-нибудь из них? Вы можете предложить калибровочные симметрии, связанные с негравитационными силами, обсуждавшиеся в главе 5. Да, это несомненные симметрии в природе, но они являются более абстрактными по своему характеру; в данный момент мы хотим сконцентрировать наше внимание на тех видах симметрии, которые имеют непосредственное отношение к пространству, времени или движению. Если добавить это условие, по всей вероятности, вам не удастся предложить чего-либо нового. На самом деле в 1967 г. физики Сидни Коулмен и Джеффри Мандула сумели доказать, что никакие другие виды симметрии, связанные с пространством, временем или движением, не могут сочетаться с принципами симметрии, рассмотренными выше, и приводить к теории, имеющей какое-либо отношение к нашему миру.

Однако впоследствии более тщательное изучение этой теоремы, основанное на догадках ряда физиков, позволило обнаружить одну небольшую лазейку: результат Коулмена-Мандулы не охватывает симметрии, связанные с понятием, известным как спин.

Элементарные частицы, например электрон, могут вращаться вокруг атомных ядер подобно тому, как Земля вращается вокруг Солнца. Однако может показаться, что в традиционной точечной модели электрона нет аналога вращению Земли вокруг своей оси. Когда объект вращается, точки, расположенные на оси вращения, подобно центральной точке фрисби-диска, остаются неподвижными. Но если какой-нибудь объект является действительно точечным, у него нет «других точек», которые не находились бы на оси вращения. В результате может показаться, что такого понятия, как вращение точечного объекта, попросту не существует. Много лет назад исследование этого вопроса привело к открытию еще одного поразительного квантового эффекта.

В 1925 г. голландские физики Джордж Уленбек и Сэмюэль Гоудсмит осознали, что многие удивительные результаты, относящиеся к свойствам излучаемого и поглощаемого атомами света могут быть объяснены, если предположить, что электроны обладают некоторыми весьма специфичными магнитными свойствами. Примерно за сто лет до этого французский физик Андре-Мари Ампер показал, что магнетизм обязан своим происхождением движению электрических зарядов. Уленбек и Гоудсмит исследовали этот факт и установили, что только один конкретный вид движения электрона может привести к появлению магнитных свойств, на которые указывали экспериментальные данные: это было вращательное движение — спин электрона. Вопреки канонам классической физики, Уленбек и Гоудсмит провозгласили, что электрон, подобно Земле, может кружить по орбите и одновременно вращаться вокруг собственной оси.

Считали ли Уленбек и Гоудсмит, что электрон действительна вращается вокруг своей оси? И да, и нет. На самом деле их работа показала, что существует квантово-механическое понятие спина, которое в определенной степени напоминает вращение объекта вокруг собственной оси, но которое, по сути, представляет квантово-механическое явление. Это одно из тех свойств микромира, которое не имеет аналога в классической физике, а является экспериментально подтверждаемой квантовой особенностью. Представьте себе, например, вращающегося фигуриста. Когда он прижимает руки к телу, его вращение ускоряется, когда разводит руки в стороны — вращение замедляется. Однако рано или поздно, в зависимости от того, с какой энергией он начал свое вращение, его движение замедлится, и он остановится. Не так обстоят дела со спином, открытым Уленбеком и Гоудсмитом. Согласно их работе и данным последующих исследований, каждый электрон во Вселенной всегда вращается с постоянной и никогда не меняющейся скоростью. Спин электрона не является промежуточным состоянием движения, которое мы наблюдаем в случае более привычных объектов, по тем или иным причинам пришедших во вращение. Напротив, спин электрона является внутренним, присущим электрону свойством, похожим в этом отношении на массу или электрический заряд. Если бы электрон не вращался, он не был бы электроном.

Хотя первые работы были посвящены электронам, впоследствии физики показали, что понятие спина применимо ко всем частицам вещества, образующим три семейства из табл. 1.1. Это утверждение истинно вплоть до мельчайших деталей: все частицы вещества (а также их античастицы) имеют спин, равный спину электрона. На своем специальном языке физики говорят, что все частицы вещества имеют «спин 1/2», где значение 1/2 представляет собой, грубо говоря, квантово-механическую меру скорости вращения частиц 2). Более того, физики показали, что частицы, передающие негравитационные взаимодействия, — фотоны, слабые калибровочные бозоны и глюоны — также обладают спином, который оказался в два раза больше, чем спин частиц вещества. Все эти частицы имеют «спин 1».

А как насчет гравитации? Еще до появления теории струн физики смогли установить, какой спин должен иметь гипотетический гравитон, чтобы он мог переносить гравитационное взаимодействие. Полученный ими ответ гласил: удвоенный спин фотонов, слабых калибровочных бозонов и глюонов — т. е. «спин 2».

В теории струн спин, так же как масса и константы других взаимодействий, связан с модой колебания струны. Как и в случае с точечными частицами, было бы не совсем правильно думать, что спин, который несет струна, возникает из-за того, что она действительно вращается в пространстве, однако эта картина дает хороший образ для представления. Кстати, теперь можно уточнить одно важное обстоятельство, с которым мы столкнулись ранее. В 1974 г. Шерк и Шварц провозгласили, что теория струн должна рассматриваться как квантовая теория, включающая гравитационное взаимодействие. Такой вывод стал возможен потому, что они обнаружили: в спектре колебаний струн обязательно должна присутствовать мода, которая соответствует безмассовой частице со спином 2. Но именно эти характеристики являются отличительными признаками гравитона. А где гравитон, там и гравитация.

Получив основные представления о спине, вернемся к той роли, которую он играет в качестве упомянутой в предыдущем разделе лазейки в обход теоремы Коулмена— Мандулы, касающейся возможных видов симметрии в природе.

Как мы уже подчеркивали, хотя понятие спина имеет поверхностное сходство с образом вращающегося волчка, оно имеет и значительные отличия, связанные с его квантовой природой. Открытие спина в 1925 г. показало, что имеется еще один вид вращательного движения, который попросту не существует в чисто классической Вселенной.

Это позволяет задать следующий вопрос: если обычное вращательное движение приводит к принципу симметрии, носящему название инвариантности относительно вращений («физика рассматривает все возможные направления в пространстве как равноправные»), не ведет ли это более специфическое вращательное движение еще к одному принципу симметрии законов природы? Примерно к 1971 г. физики показали, что ответ на этот вопрос положителен. Хотя полное доказательство достаточно сложно, основная идея состоит в том, что если рассматривать спин с математической точки зрения, возможна ровно одна дополнительная симметрия законов природы. Она получила название суперсимметрии3).

Суперсимметрии не может быть поставлено в соответствие простое и интуитивно понятное изменение точки зрения наблюдателя: сдвиги во времени, пространственном положении, угловой ориентации и скорости движения уже исчерпали эти возможности. Однако поскольку спин представляет собой «подобие вращательного движения, имеющее квантово-механическую природу», суперсимметрия связана с изменением точки зрения наблюдателя в «квантово-механическом расширении пространства и времени».

Кавычки здесь очень важны, поскольку последняя фраза дает только общее представление о месте суперсимметрии в общей системе принципов симметрии природы4'. Однако понимание принципа суперсимметрии является довольно сложной задачей, и мы сконцентрируем внимание на его основных следствиях, на том, согласуются ли законы природы с этим принципом. Этот вопрос гораздо легче поддается объяснению.

В начале 1970-х гг. физики пришли к выводу, что если Вселенная является суперсимметричной, частицы природы должны входить в набор наблюдаемых частиц парами, при этом спин частиц, образующих пару, должен отличаться на 1/2. Такие пары частиц — независимо от того, считаются ли они точечными (как в стандартной модели) или крошечными колеблющимися петлями — называются суперпартнерами. Поскольку частицы вещества имеют спин 1/2, а некоторые из частиц, передающих взаимодействие — спин 1, суперсимметрия приводит к выводу о наличии пар, о партнерстве частиц вещества и частиц, передающих взаимодействие. Сам по себе этот вывод выглядит весьма привлекательно с точки зрения объединения частиц в одну теорию. Проблема кроется в деталях.

К середине 1970-х гг., когда физики искали способ, который позволил бы включить суперсимметрию в стандартную модель, они обнаружили, что ни одна из известных частиц, перечисленных в табл. 1.1 и 1.2, не может быть суперпартнером для другой. Как показал тщательный теоретический анализ, если Вселенная включает принцип суперсимметрии, то каждой известной частице должна соответствовать еще не открытая частица-суперпартнер, спин которой на половину меньше, чем спин ее известного партнера. Так, партнер электрона должен иметь спин 0; эта гипотетическая частица получила название сэлектрона (сокращение от термина суперсимметричный электрон). То же самое справедливо и для других частиц вещества. Например, имеющие спин 0 гипотетические суперпартнеры нейтрино и кварков получили название снейтрино и скварков. Аналогично частицы, передающие взаимодействия, должны иметь суперпартнеров со спином 1/2. Для фотонов это будут фотино, для глюонов — глюино, для W-бозонов и Z -бозонов — вино и зино.

Таким образом, при более внимательном изучении суперсимметрия оказалась чрезвычайно неэкономичным понятием: она требовала большого количества дополнительных частиц, дублировавших список фундаментальных компонентов. Поскольку ни одна из частиц-суперпартнеров не была обнаружена, вы можете довольствоваться приведенным в главе 1 замечанием Раби по поводу открытия мюона, немного усилив его звучание: «Никто не заказывал суперсимметрию», и, без долгих рассуждений, отказаться от этого принципа симметрии. Существуют, однако, три причины, по которым многие физики твердо убеждены, что такой скоропалительный отказ от суперсимметрии был бы преждевременным. Обсудим эти причины.

Во-первых, с чисто эстетических позиций, физики не могли примириться с тем, что природа реализовала почти все, но не все математически возможные виды симметрии. Конечно, нельзя исключать возможность того, что симметрия реализуется не полностью, но это было бы так обидно. Это было бы похоже на то, как если бы Бах, написав многоголосные переплетающиеся партии, встроенные в гениальную картину музыкальной симметрии, забыл про финал, расставляющий все по своим местам.

Во-вторых, даже в стандартной модели, в теории, которая игнорирует гравитацию, многочисленные технические трудности, связанные с квантовыми эффектами, безболезненно разрешаются при использовании суперсимметрии. Основная проблема состоит в том, что каждый отдельный вид частиц вносит свой собственный вклад в микроскопический квантовый хаос. Исследуя глубины этого хаоса, физики обнаружили, что некоторые процессы, связанные со взаимодействием частиц, можно описать непротиворечивым образом только при очень точной настройке параметров стандартной модели, с точностью, превышающей 10-15, для нейтрализации наиболее разрушительных квантовых эффектов. Для сравнения: такая точность необходима для того, чтобы пуля, выпущенная из воображаемого сверхмощного ружья, попала в цель на Луне с отклонением, не превышающим размеры амебы. Хотя стандартная модель допускает регулировку параметров с такой точностью, многие физики испытывают сильное недоверие к теории, которая устроена настолько деликатно, что разваливается, если параметр, от которого она зависит, изменяется на единицу в пятнадцатом разряде после запятой5'.

Суперсимметрия радикальным образом изменяет эту ситуацию, поскольку бозоны — частицы, имеющие целочисленный спин (получившие свое название в честь индийского физика Сатьендры Бозе), и фермионы — частицы, спин которых равен половине целого (нечетного) числа (названные в честь итальянского физика Энрико Ферми), имеют тенденцию вносить такие вклады в квантовый хаос, которые взаимно сокращаются. Вклады как будто находятся на противоположных концах коромысла: когда вклад бозонов в квантовые флуктуации положителен, вклад фермионов отрицателен, и наоборот. Поскольку суперсимметрия гарантирует, что бозоны и ферм ионы существуют парами, происходит изначальное сокращение, которое существенно уменьшает самые интенсивные квантовые флуктуации. В результате непротиворечивость суперсимметричной стандартной модели, в которую включены все частицы-суперпартнеры, перестает зависеть от подозрительно тонкой регулировки значений параметров обычной стандартной модели. Хотя этот момент кажется сугубо техническим, он делает суперсимметрию очень привлекательной в глазах многих специалистов по физике элементарных частиц.

Третье косвенное доказательство в пользу суперсимметрии связано с понятием великого объединения. Одно из самых загадочных свойств четырех фундаментальных взаимодействий природы состоит в огромных различиях интенсивности этих взаимодействий. Интенсивность электромагнитных сил не превышает одного процента от интенсивности сильного взаимодействия. Слабое взаимодействие примерно в тысячу раз слабее электромагнитного, а интенсивность гравитационных сил слабее еще в несколько сотен миллионов миллиардов миллиардов миллиардов (10-35) раз. Следуя удостоенной Нобелевской премии пионерской работе Глэшоу, Салама и Вайнберга, установившей глубокую связь между электромагнитным и слабым взаимодействием (см. главу 5), Глэшоу и его коллега по Гарвардскому университету Говард Джорджи предположили, что подобную связь можно протянуть и к сильному взаимодействию. Их работа, предлагавшая «великое объединение» трех из четырех взаимодействий, имела одно существенное отличие от электрослабой теории. Электромагнитное и слабое взаимодействия выкристаллизовались из более симметричного состояния, когда температура Вселенной упала примерно до миллиона миллиардов градусов выше абсолютного нуля (1015 К). Джорджи и Глэшоу показали, что объединение с сильным взаимодействием становится очевидным только при температуре, которая еще в десять триллионов раз выше, примерно при десяти миллиардах миллиардов миллиардов миллиардов градусов выше абсолютного нуля (при 1028 К). С точки зрения энергии это примерно в миллион миллиардов раз больше массы протона, или примерно на четыре порядка меньше планковской массы. Джорджи и Глэшоу дерзко направили теоретическую физику в область энергий, на много порядков превышающих те, с которыми исследователи отваживались иметь дело раньше.

Следующая работа, выполненная Джорджи, Хелен Куинн и Вайнбергом в 1974 г. в Гарварде, с еще большей очевидностью показала возможность объединения негравитационных взаимодействий в рамках теории великого объединения. Поскольку их вклад продолжает играть важную роль в объединении взаимодействий и исследовании суперсимметрии природы, потратим немного времени на то, чтобы объяснить его более подробно.

Мы знаем, что электромагнитное притяжение между двумя противоположно заряженными частицами и гравитационное притяжение между двумя массивными телами увеличивается при уменьшении расстояния между объектами. Это простые и хорошо известные факты из классической физики. Сюрпризы начинаются, когда мы исследуем влияние квантовой физики на интенсивность взаимодействий. Почему вообще квантовая механика оказывает какое-либо влияние на эти явления? Ответ опять же связан с квантовыми флуктуациями. Когда мы исследуем электрическое поле электрона, на самом деле мы исследуем его сквозь «туман» электрон-позитронных пар, непрерывно рождающихся и аннигилирующих в окружающей его области пространства. Некоторое время назад физики осознали, что этот кипящий туман микроскопических флуктуации маскирует истинную напряженность поля, создаваемого электроном, подобно тому, как туман в природе ослабляет луч маяка. По мере того, как мы приближаемся к электрону, мы проникаем все глубже в обволакивающий его туман, состоящий из частиц и античастиц, и поэтому такой туман будет оказывать меньшее влияние на наши наблюдения. Из этого следует, что по мере приближения к электрону напряженность создаваемого им электрического поля будет возрастать.

Физики отличают это возрастание напряженности при приближении к электрону, связанное с квантовыми эффектами, от собственной напряженности электромагнитного взаимодействия, возрастающей с уменьшением расстояния. Таким образом, напряженность возрастает не просто потому, что мы приближаемся к электрону, но также вследствие того, что становится видимым собственное электрическое поле электрона. Хотя мы рассматривали электрон, на самом деле эти выводы применимы к любым частицам, несущим электрический заряд. Их можно суммировать утверждением, что квантовые эффекты ведут к росту электромагнитных сил при уменьшении расстояния.

А что можно сказать о других взаимодействиях, описываемых стандартной моделью? Как изменяется их интенсивность с изменением расстояния? В 1973 г. Гросс и Фрэнк Вильчек из Принстона и независимо от них Дэвид Политцер из Гарварда исследовали этот вопрос и получили удивительный результат. Квантовое облако, состоящее из рождающихся и аннигилирующих частиц, увеличивает интенсивность сильного и слабого взаимодействия. Это означает, что когда мы исследуем эти взаимодействия на более близких расстояниях, мы проникаем глубже в кипящее облако квантовых флуктуации, и, следовательно, увеличение интенсивности ощущается менее заметно. Таким образом, интенсивность этих видов взаимодействия уменьшается при уменьшении расстояния, на котором мы их исследуем.

Джорджи, Куинн и Вайнберг использовали эти идеи и довели их до замечательного финала. Они показали, что если аккуратно учесть влияние всех этих квантовых флуктуации, то мы увидим, что интенсивности всех трех негравитационных взаимодействий станут сближаться. Хотя интенсивности этих трех видов взаимодействий очень сильно различаются на масштабах расстояний, доступных современной технике, согласно выводам Джорджи, Куинн и Вайнберга, это различие связано с различным влиянием, которое оказывает на них «туман» квантовых флуктуации. Их расчеты показали, что если проникнуть сквозь этот туман и исследовать взаимодействия не в обычных для нас масштабах, а на расстояниях, составляющих примерно одну сотую от миллиардной миллиардной миллиардной (10-29) доли сантиметра (приблизительно в десять тысяч раз превышающем планковскую длину), интенсивности всех трех негравитационных взаимодействий окажутся одинаковыми.

Высокие энергии, которые исследуются на таких малых расстояниях, значительно превышают те, с которыми мы обычно имеем дело, однако такие энергии были характерными для бурной и раскаленной Вселенной в момент, когда ее возраст составлял примерно одну тысячную от одной триллионной триллионной триллионной (10-39) доли секунды, а ее температура, как упоминалось выше — около 1028 К. Эти теоретические работы показали, что примерно так же, как набор самых различных ингредиентов — кусков металла, дерева, горных пород, минералов и т. п. — сплавляется в единое целое и образует однородную, гомогенную плазму при нагреве до достаточно высокой температуры, сильное, слабое и электромагнитное взаимодействия при такой огромной температуре сливаются в одно величественное взаимодействие. Схематически это показано на рис. 7.1 6).

Рис. 7.1. Интенсивность трех негравитационных взаимодействий при уменьшении расстояния или (что эквивалентно) при увеличении энергии.

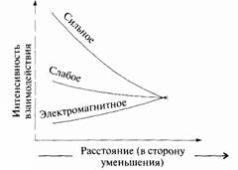Хотя у нас нет устройств, с помощью которых можно было бы производить измерения на столь малых расстояниях или воспроизводить столь высокие температуры, за время, прошедшее с 1974 г., экспериментаторам удалось существенно уточнить значения интенсивности трех негравитационных взаимодействий в обычных условиях. Эти данные, являющиеся начальными точками на трех кривых изменения интенсивности взаимодействий, показанных на рис. 7.1, представляют собой исходные данные для квантово-механических расчетов, выполненных Джорджи, Куинн и Вайнбергом. В 1991 г. Уго Амальди из ЦЕРНа, Вим де Боер и Герман Фюрстенау из университета Карлсруэ в Германии пересчитали результаты Джорджи, Куинн и Вайнберга с использованием новых экспериментальных данных и продемонстрировали два замечательных факта. Во-первых, интенсивность трех негравитационных взаимодействий почти (но не абсолютно) одинакова в масштабе малых расстояний (соответственно, высоких энергий и высоких температур), как показано на рис. 7.2.

Рис. 7.2. Уточнение расчета интенсивностей взаимодействий показало, что без суперсимметрии они очень близки, но не совпадают.

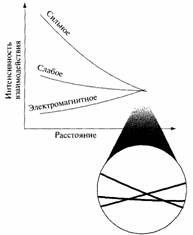Во-вторых, это незначительное, но несомненное различие в интенсивности исчезает при включении суперсимметрии. Причина состоит в том, что новые частицы-суперпартнеры, существования которых требует суперсимметрия, дают дополнительные квантовые флуктуации достаточной величины, чтобы интенсивности взаимодействий стали одинаковыми.

Для большинства физиков чрезвычайно трудно поверить в то, что природа могла выбрать взаимодействия таким образом, чтобы на микроскопическом уровне они были почти, но не в точности равны. Это все равно, как если бы вы собирали головоломку и увидели, что последний фрагмент имеет немного не ту форму, которая позволила бы ему занять последнее остающееся свободным место. Суперсимметрия искусно изменяет форму этого фрагмента, и все части головоломки встают на свои места.

Другой аспект этих последних достижений связан с тем, что они дают возможный ответ на вопрос, почему до сих пор не открыта ни одна частица-суперпартнер. Расчеты, подтвердившие равенство интенсивности взаимодействий, а также ряд других исследований, выполненных физиками, показали, что частицы-суперпартнеры должны быть намного тяжелее, чем все открытые до сих пор частицы. Хотя точный прогноз дать пока невозможно, проведенные исследования показывают, что частицы-суперпартнеры должны быть как минимум в тысячу раз тяжелее протона. Это объясняет, почему такие частицы до сих пор не обнаружены: даже самые современные ускорители не способны развивать такие энергии. В главе 9 мы вернемся к вопросу о перспективах экспериментальной проверки того, является ли суперсимметрия реальным свойством нашего мира.

Конечно, приведенные доводы в пользу того, чтобы принять суперсимметрию или, по крайней мере, не отвергать такой возможности, не являются неоспоримыми. Мы описали, как суперсимметрия придает нашим теориям наиболее симметричный вид, но вы можете возразить, что мироздание, возможно, вовсе не стремится принять наиболее симметричную форму, достижимую с математической точки зрения. Мы обратили ваше внимание на важный технический момент, состоящий в том, что суперсимметрия избавляет нас от необходимости детальной подгонки параметров стандартной модели для преодоления ряда тонких проблем в квантовой теории, но вы можете возразить, что истинная теория, описывающая явления природы, вполне может балансировать на тонкой грани между непротиворечивостью и саморазрушением. Мы показали, что на ничтожно малых расстояниях суперсимметрия изменяет интенсивность трех негравитационных взаимодействий в точности так, чтобы они могли слиться в одно великое объединенное взаимодействие, но вы, опять же, можете возразить, что в устройстве мироздания нет ничего, что диктовало бы необходимость совпадения интенсивности этих взаимодействий на микроскопическом масштабе. Наконец, вы можете предположить, что частицы-суперпартнеры до сих пор не обнаружены просто потому, что наша Вселенная не является суперсимметричной и, следовательно, частицы-суперпартнеры не существуют.

Никто не может опровергнуть ни одно из этих возражений. Однако доводы, говорящие в пользу суперсимметрии, необычайно усиливаются, если мы рассмотрим ее роль в теории струн.

Первоначальный вариант теории струн, начало которой было положено работой Венециано в конце 1960-х гг., содержал все виды симметрии, которые обсуждались в первых пунктах этой главы, но не включал суперсимметрию (которая в то время еще не была открыта). Эта первая теория, базировавшаяся на концепции струн, называлась теорией бозонных струн. Слово бозонная указывает на то, что все моды колебаний бозонной струны обладали целочисленным спином: в этой теории не было фермионных мод, т. е. мод, спин которых отличался бы от целого числа на половину единицы. Это приводило к двум проблемам.

Во-первых, если назначением теории струн было описание всех взаимодействий и всех видов материи, она должна была каким-то образом включать фермионные моды колебаний, поскольку все известные частицы вещества имеют спин 1/2. Вторая, гораздо более серьезная проблема была связана с существованием в теории бозонных струн еще одной моды колебаний, масса которой (или, точнее, квадрат массы) была отрицательной, — так называемого тахиона. Возможность того, что в дополнение к более привычным частицам с положительными массами наш мир может содержать тахионы, изучалась физиками еще до появления теории струн, однако их работы показали, что создать непротиворечивую теорию, включающую тахионы, чрезвычайно трудно, если вообще возможно. Аналогичным образом физики испробовали самые фантастические способы, пытаясь придать смысл экзотической идее тахионной моды в контексте теории струн, но все попытки оказались безуспешными. Эти две проблемы показали, что хотя теория бозонных струн была весьма интересна, в ней определенно не хватало каких-то существенных элементов.

В 1971 г. Пьер Рамон из университета штата Флорида принял вызов и модифицировал теорию бозонных струн, включив в нее фермионные моды колебаний. Его работа и результаты, полученные позднее Шварцем и Андре Невье, положили начало новой версии теории струн. Ко всеобщему удивлению, в эту новую теорию бозонные и фермионные моды колебаний входили парами. Для каждой бозонной моды существовала соответствующая фермионная, и наоборот. К 1977 г. работы Фердинандо Льоцци из университета Турина, а также работы Шерка и Дэвида Олива из Имперского колледжа, показали истинный смысл этого группирования в пары. Новая теория струн включала суперсимметрию, и то, что бозонные и фермионные моды колебания входили парами, было отражением высокой степени симметрии этой теории. В этот момент родилась суперсимметричная теория струн — теория суперструн. Работы Льоцци, Шерка и Олива дали еще один очень важный результат: они показали, что вызывавшая беспокойство тахионная мода колебаний бозонных струн не свойственна суперструнам. Части конструкции теории струн постепенно вставали на свои места.

Однако изначально основное влияние работы Рамона, Невье и Шварца оказали не на теорию струн. К 1973 г. физики Джулиус Весе и Бруно Зумино осознали, что суперсимметрия — новый вид симметрии, появившийся при изменении формулировки теории струн, — применима и к теориям, основанным на точечной модели частиц. Они быстро предприняли важные шаги в направлении включения суперсимметрии в систему квантовой теории поля, основанной на точечной модели частиц. А поскольку в это время квантовая теория поля была основным объектом исследования специалистов по физике элементарных частиц (при этом теория струн все более прочно занимала место на переднем краю исследований), за достижениями Весса и Зумино последовало огромное количество исследований в области, которая получила название суперсимметричной квантовой теории поля. Суперсимметричная стандартная модель, которую мы обсуждали в предыдущем разделе, была одним из главных теоретических достижений в этом направлении. Таким образом, благодаря зигзагам на пути развития теории струн, в большом долгу перед ней оказалась даже теория, основанная на точечной модели частиц.

С возрождением теории суперструн в середине 1980-х гг. суперсимметрия вновь вернулась в лоно, где она была впервые открыта. И в этом контексте свидетельства в пользу суперсимметрии выходят далеко за пределы того, о чем говорилось в предыдущем разделе. Теория струн представляет собой единственный известный нам способ объединения общей теории относительности и квантовой механики. При этом только суперсимметричная версия теории струн позволяет избежать фатальной тахионной проблемы и содержит фермионные моды колебаний, соответствующие частицам вещества, составляющим окружающий нас мир. Таким образом, суперсимметрия идет рука об руку с теорией струн и тем, что она дает для квантовой теории гравитации и для решения грандиозной задачи великого объединения всех видов взаимодействия и всех частиц материи. Физики полагают, что если теория струн верна, то верна и идея суперсимметрии.

Однако до середины 1990-х гг. в суперсимметричной теории струн была одна весьма серьезная проблема.

Если кто-нибудь скажет вам, что он разгадал тайну судьбы Амелии Эрхарт (Амелия Эрхарт (Amelia Earhart) — первая американка, совершившая в одиночку перелет через Атлантический океан. В 1935 г. совершила рекордный одиночный перелет с Гавайских островов в Калифорнию. Пропала без вести в районе Новой Гвинеи при попытке совершить первый перелет вокруг света. — Прим. перев.), наверное, сначала вы отнесетесь к его словам скептически, но если он предоставит вам подтвержденные документами серьезные свидетельства, вы, скорее всего, дослушаете этого человека до конца и, кто знает, может быть, он даже убедит вас. Но что вы подумаете, если спустя мгновение он сообщит вам, что у него есть еще одно объяснение? Вы терпеливо слушаете и, к своему удивлению, обнаруживаете, что альтернативное объяснение столь же хорошо документировано и продумано, как и первое. После завершения рассказа о новом объяснении вам будет представлено третье, четвертое и даже пятое объяснения, и каждое из них будет отличаться от предыдущих, но будет столь же хорошо подкреплено доказательствами. Нет никаких сомнений, что к концу вашей беседы вы будете чувствовать себя не ближе к решению загадки судьбы Амелии Эрхарт, чем вы были вначале. В области фундаментальных объяснений слово «больше» определенно означает «меньше».

К 1985 г. теория струн, несмотря на заслуженное восхищение, которое она вызывала, начала звучать подобно чересчур рьяному эксперту по судьбе Амелии Эрхарт. Причина состояла в том, что к 1985 г. физики осознали, что суперсимметрия, являющаяся центральным звеном теории струн, на самом деле может быть включена в нее не одним, а пятью различными способами. Каждый метод приводил к образованию пар бозонных и фермионных мод колебания, но детали такой группировки, а также многочисленные другие свойства получавшихся теорий, существенно различались. Хотя названия, которые получили эти теории, не имеют большой важности, потрудимся запомнить, что это были: теория струн типа I, теория струн типа IIА, теория струн типа IIВ, теория гетеротических струн 0(32) (произносится «о тридцать два»), а также теория гетеротических струн E8 х Е8 (произносится «е восемь на е восемь»). Все особенности теории струн, которые мы обсуждали до сих пор, справедливы для каждой из этих теорий, они различаются только в более тонких деталях.

Иметь пять различных версий того, что считалось теорией всего, т. е. возможной конечной объединяющей теорией, было слишком много для специалистов по теории струн. Как существует только одно правдивое объяснение того, что случилось с Амелией Эрхарт (независимо от того, узнаем ли мы его когда-нибудь), так и наиболее глубокое, фундаментальное понимание устройства мироздания, согласно нашим представлениям, может быть только одним. Мы живем в одной Вселенной и ожидаем существование только одного объяснения.

Одно из решений этой проблемы может быть следующим. Хотя у нас есть пять различных теорий суперструн, четыре лишних можно отбросить с помощью экспериментальных исследований, и в результате останется одна, истинная формулировка. Но даже если это удалось бы сделать, у нас все равно остался бы саднящий вопрос — откуда возникли другие теории. Немного перефразируя Виттена: «Если одна из пяти теорий описывает нашу Вселенную, то кто живет в четырех остальных?»7) Мечта физика состоит в том, чтобы его поиск окончательных ответов привел к одному, уникальному, совершенно неизбежному выводу. В идеале окончательная теория, будь то теория струн или что-то иное, должна быть такой, какова она есть, просто потому, что другого способа не существует. Если бы мы открыли, что существует только одна логически непротиворечивая теория, объединяющая основные компоненты общей теории относительности и квантовой механики, многие почувствовали бы, что достигнуто глубочайшее понимание того, почему мироздание имеет те свойства, которые оно имеет. Короче говоря, наступили бы райские времена единой теории8).

Как мы увидим в главе 12, последние исследования в теории суперструн позволили сделать гигантский шаг в направлении этой единой утопии, показав, что пять различных теорий в действительности представляют собой пять различных способов описания одной и той же объединяющей теории. Теория суперструн имеет единое генеалогическое древо.

Все, похоже, постепенно становится на свои места. Однако, как мы увидим в следующей главе, объединение в рамках теории струн требует еще одного, более радикального отказа от наших обычных представлений.